
En geometría , se dice que dos o más objetos son concéntricos cuando comparten el mismo centro . Cualquier par de objetos (posiblemente diferentes) con centros bien definidos puede ser concéntrico, incluidos círculos , esferas , polígonos regulares , poliedros regulares , paralelogramos, conos, secciones cónicas y cuádricas. [1]
Los objetos geométricos son coaxiales si comparten el mismo eje (línea de simetría). Los objetos geométricos con un eje bien definido incluyen círculos (cualquier línea que pase por el centro), esferas, cilindros , [2] secciones cónicas y superficies de revolución.
Los objetos concéntricos suelen formar parte de la amplia categoría de patrones en espiral , que también incluye espirales (una curva que emana de un punto y se aleja a medida que gira alrededor del punto).
En el plano euclidiano , dos círculos que son concéntricos necesariamente tienen radios diferentes entre sí. [3] Sin embargo, los círculos en el espacio tridimensional pueden ser concéntricos y tener el mismo radio entre sí, pero sin embargo ser círculos diferentes. Por ejemplo, dos meridianos diferentes de un globo terrestre son concéntricos entre sí y con el globo de la Tierra (aproximadamente como una esfera). De manera más general, cada dos círculos máximos en una esfera son concéntricos entre sí y con la esfera. [4]
Por el teorema de Euler en geometría sobre la distancia entre el circuncentro y el incentro de un triángulo, dos círculos concéntricos (siendo esa distancia cero) son el circuncentro y el incírculo de un triángulo si y sólo si el radio de uno es el doble del radio del otro, en cuyo caso el triángulo es equilátero . [5] : p. 198
El círculo circunscrito y el círculo inscrito de un n -gono regular , y el propio n -gono regular, son concéntricos. Para conocer la relación entre el radio circunscrito y el radio inscrito para varios n , consulte Polígono bicéntrico#Polígonos regulares . Lo mismo puede decirse de la esfera interna , la esfera media y la esfera circunscrita de un poliedro regular .
La región del plano entre dos círculos concéntricos es un anillo , y análogamente la región del espacio entre dos esferas concéntricas es una envoltura esférica . [6]
Para un punto dado c en el plano, el conjunto de todos los círculos que tienen c como centro forma un lápiz de círculos . Cada dos círculos en el lápiz son concéntricos y tienen radios diferentes. Cada punto en el plano, excepto el centro compartido, pertenece exactamente a uno de los círculos en el lápiz. Cada dos círculos disjuntos, y cada lápiz hiperbólico de círculos, pueden transformarse en un conjunto de círculos concéntricos mediante una transformación de Möbius . [7] [8]
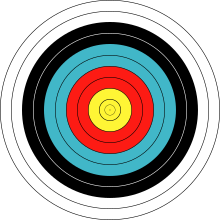
Las ondas que se forman al dejar caer un objeto pequeño en agua quieta forman naturalmente un sistema en expansión de círculos concéntricos. [9] Los círculos espaciados uniformemente en los objetivos utilizados en el tiro con arco [10] o deportes similares proporcionan otro ejemplo familiar de círculos concéntricos.
El cable coaxial es un tipo de cable eléctrico en el que el núcleo combinado neutro y de tierra rodea completamente el o los núcleos activos en un sistema de carcasas cilíndricas concéntricas. [11]
El Mysterium Cosmographicum de Johannes Kepler imaginó un sistema cosmológico formado por poliedros y esferas regulares concéntricos. [12]
Los círculos concéntricos se han utilizado en superficies de armas de fuego como un medio para mantener la lubricación o reducir la fricción en los componentes, de forma similar a las joyas . [13]
Los círculos concéntricos también se encuentran en las miras dióptricas , un tipo de miras mecánicas que se encuentran comúnmente en los rifles de tiro al blanco. Por lo general, cuentan con un disco grande con un orificio de diámetro pequeño cerca del ojo del tirador y una mira de globo frontal (un círculo contenido dentro de otro círculo, llamado túnel ). Cuando estas miras están correctamente alineadas, el punto de impacto estará en el medio del círculo de la mira frontal.
Esferas: Apóstol (2013)
Polígonos regulares: Hardy, Godfrey Harold (1908), Un curso de matemáticas puras, The University Press, pág. 107
Poliedros regulares: Gillard, Robert D. (1987), Química de coordinación integral: teoría y antecedentes, Pergamon Press, págs. 137, 139, ISBN 9780080262321.