Función de supervivencia

La función de supervivencia es una función que proporciona la probabilidad de que un paciente, dispositivo u otro objeto de interés sobreviva más allá de un tiempo determinado. ^[1] La función de supervivencia también se conoce como función de supervivencia ^[2] o función de confiabilidad . ^[3] El término función de confiabilidad es común en ingeniería, mientras que el término función de supervivencia se utiliza en una gama más amplia de aplicaciones, incluida la mortalidad humana. La función de supervivencia es la función de distribución acumulativa complementaria de la vida útil. A veces, las funciones de distribución acumulativa complementarias se denominan funciones de supervivencia en general.

Definición

Sea el tiempo de vida T una variable aleatoria continua con función de riesgo acumulativo F ( t ) y función de riesgo f( t ) en el intervalo [0,∞). Su función de supervivencia o función de confiabilidad es:

S(t)=P(\{T>t\})=\int _{t}^{\infty }f(u)\,du=1-F(t).

Ejemplos de funciones de supervivencia

Los gráficos que se muestran a continuación muestran ejemplos de funciones de supervivencia hipotéticas. El eje x representa el tiempo. El eje y representa la proporción de sujetos que sobreviven. Los gráficos muestran la probabilidad de que un sujeto sobreviva más allá del tiempo t.

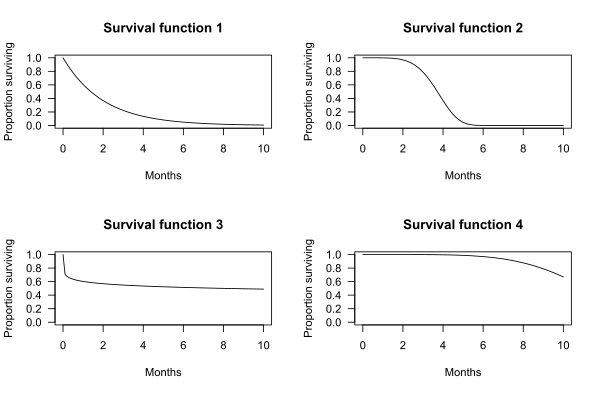
Por ejemplo, para la función de supervivencia 1, la probabilidad de sobrevivir más de t = 2 meses es 0,37. Es decir, el 37% de los sujetos sobreviven más de 2 meses.

Para la función de supervivencia 2, la probabilidad de sobrevivir más de t = 2 meses es de 0,97. Es decir, el 97% de los sujetos sobreviven más de 2 meses.

La supervivencia media se puede determinar a partir de la función de supervivencia: La supervivencia media es el punto en el que la función de supervivencia interseca el valor 0,5. ^[4] Por ejemplo, para la función de supervivencia 2, el 50% de los sujetos sobreviven 3,72 meses. La supervivencia media es, por tanto, 3,72 meses.

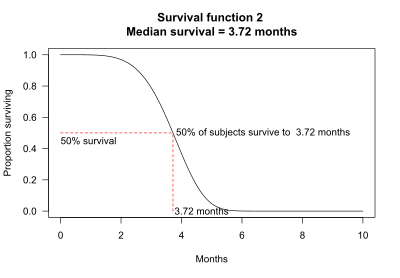
En algunos casos, la supervivencia media no se puede determinar a partir del gráfico. Por ejemplo, para la función de supervivencia 4, más del 50 % de los sujetos sobreviven más allá del período de observación de 10 meses.

La función de supervivencia es una de las diversas formas de describir y mostrar los datos de supervivencia. Otra forma útil de mostrar los datos es un gráfico que muestra la distribución de los tiempos de supervivencia de los sujetos. Olkin, ^[5] página 426, da el siguiente ejemplo de datos de supervivencia. Se registró el número de horas entre fallos sucesivos de un sistema de aire acondicionado. El tiempo entre fallos sucesivos es 1, 3, 5, 7, 11, 11, 11, 12, 14, 14, 14, 16, 16, 20, 21, 23, 42, 47, 52, 62, 71, 71, 87, 90, 95, 120, 120, 225, 246 y 261 horas. El tiempo medio entre fallos es 59,6. Este valor medio se utilizará en breve para ajustar una curva teórica a los datos. La siguiente figura muestra la distribución del tiempo entre fallas. Las marcas de verificación azules debajo del gráfico son las horas reales transcurridas entre fallas sucesivas.

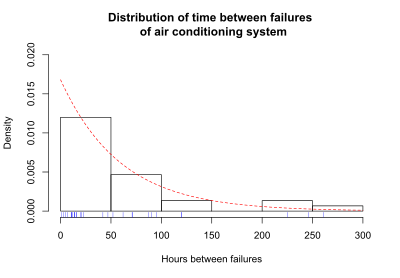
La distribución de los tiempos de falla se superpone con una curva que representa una distribución exponencial. Para este ejemplo, la distribución exponencial se aproxima a la distribución de los tiempos de falla. La curva exponencial es una distribución teórica ajustada a los tiempos de falla reales. Esta curva exponencial particular se especifica mediante el parámetro lambda, λ = 1/(tiempo medio entre fallas) = 1/59,6 = 0,0168. La distribución de los tiempos de falla se denomina función de densidad de probabilidad (pdf), si el tiempo puede tomar cualquier valor positivo. En las ecuaciones, la pdf se especifica como f(t). Si el tiempo solo puede tomar valores discretos (como 1 día, 2 días, etc.), la distribución de los tiempos de falla se denomina función de masa de probabilidad (pmf). La mayoría de los métodos de análisis de supervivencia suponen que el tiempo puede tomar cualquier valor positivo y f(t) es la pdf. Si el tiempo entre las fallas observadas del aire acondicionado se aproxima utilizando la función exponencial, entonces la curva exponencial da la función de densidad de probabilidad, f(t), para los tiempos de falla del aire acondicionado.

Otra forma útil de mostrar los datos de supervivencia es un gráfico que muestra las fallas acumuladas hasta cada punto de tiempo. Estos datos se pueden mostrar como el número acumulado o la proporción acumulada de fallas hasta cada momento. El gráfico a continuación muestra la probabilidad acumulada (o proporción) de fallas en cada momento para el sistema de aire acondicionado. La línea escalonada en negro muestra la proporción acumulada de fallas. Para cada paso hay una marca azul en la parte inferior del gráfico que indica un tiempo de falla observado. La línea roja suave representa la curva exponencial ajustada a los datos observados.

Un gráfico de la probabilidad acumulada de fallas hasta cada punto de tiempo se denomina función de distribución acumulada o CDF. En el análisis de supervivencia, la función de distribución acumulada proporciona la probabilidad de que el tiempo de supervivencia sea menor o igual a un tiempo específico, t.

Sea T el tiempo de supervivencia, que es cualquier número positivo. Un tiempo particular se designa con la letra minúscula t. La función de distribución acumulativa de T es la función

F(t)=\nombre del operador {P} (T\leq t),

donde el lado derecho representa la probabilidad de que la variable aleatoria T sea menor o igual a t . Si el tiempo puede tomar cualquier valor positivo, entonces la función de distribución acumulativa F(t) es la integral de la función de densidad de probabilidad f(t).

Para el ejemplo del aire acondicionado, el gráfico de la CDF a continuación ilustra que la probabilidad de que el tiempo hasta la falla sea menor o igual a 100 horas es 0,81, según lo estimado utilizando la curva exponencial ajustada a los datos.

Una alternativa a graficar la probabilidad de que el tiempo de falla sea menor o igual a 100 horas es graficar la probabilidad de que el tiempo de falla sea mayor a 100 horas. La probabilidad de que el tiempo de falla sea mayor a 100 horas debe ser 1 menos la probabilidad de que el tiempo de falla sea menor o igual a 100 horas, porque la probabilidad total debe sumar 1.

Esto da

P(tiempo de falla > 100 horas) = 1 - P(tiempo de falla < 100 horas) = 1 – 0,81 = 0,19.

Esta relación se generaliza a todos los tiempos de falla:

P(T > t) = 1 - P(T < t) = 1 – función de distribución acumulativa.

Esta relación se muestra en los gráficos siguientes. El gráfico de la izquierda es la función de distribución acumulativa, que es P(T < t). El gráfico de la derecha es P(T > t) = 1 - P(T < t). El gráfico de la derecha es la función de supervivencia, S(t). El hecho de que S(t) = 1 – CDF es la razón por la que otro nombre para la función de supervivencia es función de distribución acumulativa complementaria.

Funciones de supervivencia paramétricas

En algunos casos, como en el ejemplo del aire acondicionado, la distribución de los tiempos de supervivencia se puede aproximar bien mediante una función como la distribución exponencial. Varias distribuciones se utilizan comúnmente en el análisis de supervivencia, incluidas la exponencial, Weibull, gamma, normal, log-normal y log-logística. ^[3]^[6] Estas distribuciones se definen mediante parámetros. La distribución normal (gaussiana), por ejemplo, se define mediante los dos parámetros media y desviación estándar. Las funciones de supervivencia que se definen mediante parámetros se denominan paramétricas.

En los cuatro gráficos de funciones de supervivencia que se muestran arriba, la forma de la función de supervivencia está definida por una distribución de probabilidad particular: la función de supervivencia 1 está definida por una distribución exponencial, 2 está definida por una distribución de Weibull, 3 está definida por una distribución log-logística y 4 está definida por otra distribución de Weibull.

Función de supervivencia exponencial

En una distribución de supervivencia exponencial, la probabilidad de fallo es la misma en cada intervalo de tiempo, sin importar la edad del individuo o del dispositivo. Este hecho conduce a la propiedad de "falta de memoria" de la distribución de supervivencia exponencial: la edad de un sujeto no tiene efecto sobre la probabilidad de fallo en el siguiente intervalo de tiempo. La distribución exponencial puede ser un buen modelo para la vida útil de un sistema en el que las piezas se reemplazan a medida que fallan. ^[7] También puede ser útil para modelar la supervivencia de organismos vivos en intervalos cortos. No es probable que sea un buen modelo de la vida útil completa de un organismo vivo. ^[8] Como señalan Efron y Hastie ^[9] (p. 134), "si las vidas humanas fueran exponenciales no habría gente vieja o joven, solo gente afortunada o desafortunada".

Función de supervivencia de Weibull

Un supuesto clave de la función de supervivencia exponencial es que la tasa de riesgo es constante. En un ejemplo dado anteriormente, la proporción de hombres que mueren cada año era constante en un 10%, lo que significa que la tasa de riesgo era constante. El supuesto de riesgo constante puede no ser apropiado. Por ejemplo, entre la mayoría de los organismos vivos, el riesgo de muerte es mayor en la vejez que en la mediana edad, es decir, la tasa de riesgo aumenta con el tiempo. Para algunas enfermedades, como el cáncer de mama, el riesgo de recurrencia es menor después de 5 años, es decir, la tasa de riesgo disminuye con el tiempo. La distribución de Weibull extiende la distribución exponencial para permitir tasas de riesgo constantes, crecientes o decrecientes.

Otras funciones de supervivencia paramétricas

Existen otras funciones de supervivencia paramétricas que pueden proporcionar un mejor ajuste a un conjunto de datos en particular, incluidas las funciones normales, lognormales, loglogísticas y gamma. La elección de la distribución paramétrica para una aplicación particular se puede realizar mediante métodos gráficos o pruebas formales de ajuste. Estas distribuciones y pruebas se describen en libros de texto sobre análisis de supervivencia. ^[1]^[3] Lawless ^[10] ofrece una amplia cobertura de los modelos paramétricos.

Las funciones de supervivencia paramétricas se utilizan habitualmente en aplicaciones de fabricación, en parte porque permiten estimar la función de supervivencia más allá del período de observación. Sin embargo, el uso adecuado de las funciones paramétricas requiere que los datos estén bien modelados por la distribución elegida. Si no se dispone de una distribución adecuada o no se puede especificar antes de un ensayo o experimento clínico, las funciones de supervivencia no paramétricas ofrecen una alternativa útil.

Funciones de supervivencia no paramétricas

Puede que no sea posible o deseable un modelo paramétrico de supervivencia. En estas situaciones, el método más común para modelar la función de supervivencia es el estimador no paramétrico de Kaplan-Meier . Este estimador requiere datos de toda la vida. Los recuentos periódicos de casos (cohortes) y muertes (y recuperación) son estadísticamente suficientes para realizar estimaciones no paramétricas de máxima verosimilitud y mínimos cuadrados de las funciones de supervivencia, sin datos de toda la vida.

Propiedades

Toda función de supervivencia es monótonamente decreciente , es decir, para todos . ${\estilo de visualización S(t)}$ $S(u)\leq S(t)$ $u>t$
- Es una propiedad de una variable aleatoria que asigna un conjunto de eventos, usualmente asociados con la mortalidad o falla de algún sistema, al tiempo .
El tiempo , , representa algún origen, típicamente el comienzo de un estudio o el inicio de la operación de algún sistema. es comúnmente la unidad, pero puede ser menor para representar la probabilidad de que el sistema falle inmediatamente después de la operación. ${\estilo de visualización t=0}$ ${\estilo de visualización S(0)}$
Dado que la CDF es una función continua hacia la derecha , la función de supervivencia también es continua hacia la derecha. $S(t)=1-F(t)$
La función de supervivencia se puede relacionar con la función de densidad de probabilidad y la función de riesgo. $f(t)$ $\lambda(t)$
- $f(t)=-S'(t)$
- $\lambda(t)=-{d\sobre {dt}}\log S(t)$

De modo que $S(t)=\exp[-\int _{0}^{t}\lambda (t')dt']$

El tiempo de supervivencia esperado $\mathbb {E}(T)=\int _{0}^{\infty }S(t)dt$

Véase también

Referencias

^ ab Kleinbaum, David G.; Klein, Mitchel (2012), Análisis de supervivencia: un texto de autoaprendizaje (tercera edición), Springer, ISBN 978-1441966452
^ Tableman, Mara; Kim, Jong Sung (2003), Análisis de supervivencia utilizando S (Primera edición), Chapman y Hall/CRC, ISBN 978-1584884088
^ abc Ebeling, Charles (2010), Introducción a la ingeniería de confiabilidad y mantenibilidad (segunda edición), Waveland Press, ISBN 978-1577666257
^ Machin, D., Cheung, Y. B., Parmar, M. (2006). Análisis de supervivencia: un enfoque práctico. Alemania: Wiley. Página 36 y siguientes Google Books
^ Olkin, Ingram; Gleser, Leon; Derman, Cyrus (1994), Modelos de probabilidad y aplicaciones (segunda edición), Macmillan, ISBN 0-02-389220-X
^ Klein, John; Moeschberger, Melvin (2005), Análisis de supervivencia: técnicas para datos censurados y truncados (segunda edición), Springer, ISBN 978-0387953991
^ Mendenhall, William; Terry, Sincich (2007), Estadística para la ingeniería y las ciencias (Quinta edición), Pearson / Prentice Hall, ISBN 978-0131877061
^ Brostrom, Göran (2012), Análisis del historial de eventos con R (primera edición), Chapman & Hall/CRC, ISBN 978-1439831649
^ Efron, Bradley; Hastie, Trevor (2016), Inferencia estadística en la era informática: algoritmos, evidencia y ciencia de datos (primera edición), Cambridge University Press, ISBN 978-1107149892
^ Lawless, Jerald (2002), Modelos estadísticos y métodos para datos de vida (segunda edición), Wiley, ISBN 978-0471372158