Spline centrípeta Catmull-Rom

Forma variante de la columna vertebral de Catmull-Rom

En gráficos por computadora , el spline centrípeto de Catmull-Rom es una variante del spline de Catmull-Rom , formulado originalmente por Edwin Catmull y Raphael Rom , ^[1] que puede evaluarse utilizando un algoritmo recursivo propuesto por Barry y Goldman. ^[2] Es un tipo de spline de interpolación (una curva que pasa por sus puntos de control) definida por cuatro puntos de control , con la curva dibujada solo desde hasta . ${\displaystyle \mathbf {P} _{0},\mathbf {P} _{1},\mathbf {P} _{2},\mathbf {P} _{3}}$ ${\displaystyle \mathbf {P} _{1}}$ ${\displaystyle \mathbf {P} _{2}}$

Interpolación spline Catmull-Rom con cuatro puntos

Definición

La formulación piramidal de Barry y Goldman

Parametrización de nudos para el algoritmo Catmull-Rom

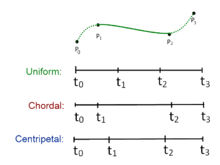
Denotemos un punto. Para un segmento de curva definido por puntos y secuencia de nudos , la spline centrípeta de Catmull-Rom se puede producir mediante: ${\displaystyle \mathbf {P} _{i}=[x_{i}\quad y_{i}]^{T}}$ ${\displaystyle \mathbf {C} }$ ${\displaystyle \mathbf {P} _{0},\mathbf {P} _{1},\mathbf {P} _{2},\mathbf {P} _{3}}$ ${\displaystyle t_{0},t_{1},t_{2},t_{3}}$

${\displaystyle \mathbf {C} ={\frac {t_{2}-t}{t_{2}-t_{1}}}\mathbf {B} _{1}+{\frac {t-t_{1}}{t_{2}-t_{1}}}\mathbf {B} _{2}}$

dónde

${\displaystyle \mathbf {B} _{1}={\frac {t_{2}-t}{t_{2}-t_{0}}}\mathbf {A} _{1}+{\frac {t-t_{0}}{t_{2}-t_{0}}}\mathbf {A} _{2}}$

${\displaystyle \mathbf {B} _{2}={\frac {t_{3}-t}{t_{3}-t_{1}}}\mathbf {A} _{2}+{\frac {t-t_{1}}{t_{3}-t_{1}}}\mathbf {A} _{3}}$

${\displaystyle \mathbf {A} _{1}={\frac {t_{1}-t}{t_{1}-t_{0}}}\mathbf {P} _{0}+{\frac {t-t_{0}}{t_{1}-t_{0}}}\mathbf {P} _{1}}$

${\displaystyle \mathbf {A} _{2}={\frac {t_{2}-t}{t_{2}-t_{1}}}\mathbf {P} _{1}+{\frac {t-t_{1}}{t_{2}-t_{1}}}\mathbf {P} _{2}}$

${\displaystyle \mathbf {A} _{3}={\frac {t_{3}-t}{t_{3}-t_{2}}}\mathbf {P} _{2}+{\frac {t-t_{2}}{t_{3}-t_{2}}}\mathbf {P} _{3}}$

y

${\displaystyle t_{i+1}=\left[{\sqrt {(x_{i+1}-x_{i})^{2}+(y_{i+1}-y_{i})^{2}}}\right]^{\alpha }+t_{i}}$

en el que va de 0 a 1 para parametrización de nudos, y con . Para el spline centrípeto Catmull-Rom, el valor de es . Cuando , la curva resultante es la spline Catmull-Rom uniforme estándar; cuando , el resultado es una spline cordal de Catmull-Rom. ${\displaystyle \alpha }$ ${\displaystyle i=0,1,2,3}$ ${\displaystyle t_{0}=0}$ ${\displaystyle \alpha }$ ${\displaystyle 0.5}$ ${\displaystyle \alpha =0}$ ${\displaystyle \alpha =1}$

Animación gif para parametrización uniforme , centrípeta y cordal del spline Catmull-Rom dependiendo del valor α

Conectando las ecuaciones spline y muestra que el valor de la curva spline en es . De manera similar, al sustituir en las ecuaciones spline se muestra que en . Esto es cierto independientemente del valor de ya que la ecuación para no es necesaria para calcular el valor de en los puntos y . ${\displaystyle t=t_{1}}$ ${\displaystyle \mathbf {A} _{1},\mathbf {A} _{2},\mathbf {A} _{3},\mathbf {B} _{1},\mathbf {B} _{2},}$ ${\displaystyle \mathbf {C} }$ ${\displaystyle t_{1}}$ ${\displaystyle \mathbf {C} =\mathbf {P} _{1}}$ ${\displaystyle t=t_{2}}$ ${\displaystyle \mathbf {C} =\mathbf {P} _{2}}$ ${\displaystyle t_{2}}$ ${\displaystyle \alpha }$ ${\displaystyle t_{i+1}}$ ${\displaystyle \mathbf {C} }$ ${\displaystyle t_{1}}$ ${\displaystyle t_{2}}$

Segmento spline Catmull-Rom centrípeto 3D .

La extensión a puntos 3D se logra simplemente considerando un punto 3D genérico y ${\displaystyle \mathbf {P} _{i}=[x_{i}\quad y_{i}\quad z_{i}]^{T}}$ ${\displaystyle \mathbf {P} _{i}}$

${\displaystyle t_{i+1}=\left[{\sqrt {(x_{i+1}-x_{i})^{2}+(y_{i+1}-y_{i})^{2}+(z_{i+1}-z_{i})^{2}}}\right]^{\alpha }+t_{i}}$

Ventajas

La spline centrípeta Catmull-Rom tiene varias propiedades matemáticas deseables en comparación con la formulación original y otros tipos de Catmull-Rom. ^[3] En primer lugar, no formará un bucle ni una autointersección dentro de un segmento de curva. En segundo lugar, la cúspide nunca se producirá dentro de un segmento de curva. En tercer lugar, sigue más estrictamente los puntos de control. ^{[4] [ vago ]}

En esta figura, hay una autointersección/bucle en la spline Catmull-Rom uniforme (verde), mientras que para la spline Catmull-Rom cordal (roja), la curva no sigue estrictamente los puntos de control.

Otros usos

En visión por computadora , se ha utilizado la spline centrípeta de Catmull-Rom para formular un modelo activo para la segmentación. El método se denomina modelo spline activo . ^[5] El modelo está diseñado sobre la base del modelo de forma activa , pero utiliza una spline centrípeta de Catmull-Rom para unir dos puntos sucesivos (el modelo de forma activa utiliza una línea recta simple), de modo que el número total de puntos necesarios para representar una forma es menos. El uso de la spline centrípeta Catmull-Rom simplifica mucho el entrenamiento de un modelo de forma y permite una mejor manera de editar un contorno después de la segmentación.

Ejemplo de código en Python

La siguiente es una implementación del spline Catmull-Rom en Python que produce el gráfico que se muestra a continuación.

importar  numpy importar  matplotlib.pyplot  como  pltCUÁDRUPLE_SIZE :  int  =  4def  num_segments ( point_chain :  tuple )  ->  int :  # Hay 1 segmento por cada 4 puntos, por lo que debemos restar 3 del número de puntos  return  len ( point_chain )  -  ( QUADRUPLE_SIZE  -  1 )def  aplanar ( lista_de_listas )  ->  lista :  # Por ejemplo, mapeo [[1, 2], [3], [4, 5]] a [1, 2, 3, 4, 5]  return  [ elem  para  lst  en  lista_de_listas  para  elem  en  primera ]def  catmull_rom_spline (  P0 :  tupla ,  P1 :  tupla ,  P2 :  tupla ,  P3 :  tupla ,  num_points :  int ,  alpha :  float  =  0.5 , ): """  Calcula los puntos en el segmento spline  : param P0, P1, P2 y P3: Los pares de puntos (x,y) que definen la spline de Catmull-Rom  :param num_points: El número de puntos a incluir en el segmento de curva resultante  :param alpha: 0,5 para la spline centrípeta, 0,0 para la spline uniforme, 1,0 para la spline cordal  :return: Los puntos  """  # Calcular t0 a t4. Luego solo calcule los puntos entre P1 y P2.  # Reformar linspace para que podamos multiplicar por los puntos P0 a P3  # y obtener un punto para cada valor de t.  def  tj ( ti :  flotante ,  pi :  tupla ,  pj :  tupla )  ->  flotante :  xi ,  yi  =  pi  xj ,  yj  =  pj  dx ,  dy  =  xj  -  xi ,  yj  -  yi  l  =  ( dx  **  2  +  dy  * *  2 )  **  0,5  retorno  ti  +  l  **  alfa t0 :  flotante  =  0.0  t1 :  flotante  =  tj ( t0 ,  P0 ,  P1 )  t2 :  flotante  =  tj ( t1 ,  P1 ,  P2 )  t3 :  flotante  =  tj ( t2 ,  P2 ,  P3 )  t  =  numpy . linspace ( t1 ,  t2 ,  núm_puntos ) . remodelar ( num_puntos ,  1 ) A1  =  ( t1  -  t )  /  ( t1  -  t0 )  *  P0  +  ( t  -  t0 )  /  ( t1  -  t0 )  *  P1  A2  =  ( t2  -  t )  /  ( t2  -  t1 )  *  P1  +  ( t  -  t1 )  /  ( t2  -  t1 )  *  P2  A3  =  ( t3  -  t )  /  ( t3  -  t2 )  *  P2  +  ( t  -  t2 )  /  ( t3  -  t2 )  *  P3  B1  =  ( t2  -  t )  /  ( t2  -  t0 )  *  A1  +  ( t  -  t0 )  /  ( t2  -  t0 )  *  A2  B2  =  ( t3  -  t )  /  ( t3  -  t1 )  *  A2  +  ( t  -  t1 )  /  ( t3  -  t1 )  *  A3  puntos  =  ( t2  -  t )  /  ( t2  -  t1 )  *  B1  +  ( t  -  t1 )  /  ( t2  -  t1 )  *  B2  puntos de retorno def  catmull_rom_chain ( puntos :  tuple ,  num_puntos :  int )  ->  lista : """  Calcula Catmull-Rom para una secuencia de puntos iniciales y devuelve la curva combinada.  :param puntos: puntos base a partir de los cuales se toman los cuádruples para el algoritmo  : parámetro num_points: el número de puntos a incluir en cada segmento de curva  :return: la cadena de todos los puntos (puntos de todos los segmentos)  """ point_quadruples = ( # Preparar entradas de función ( puntos [ idx_segment_start + d ] para d en el rango ( QUADRUPLE_SIZE )) para idx_segment_start en el rango ( num_segmentos ( puntos )) ) all_splines = ( catmull_rom_spline ( * pq , num_points ) para pq en point_quadruples ) return flatten ( all_splines )                           si  __nombre__  ==  "__main__" :  PUNTOS :  tupla  =  (( 0 ,  1.5 ),  ( 2 ,  2 ),  ( 3 ,  1 ),  ( 4 ,  0.5 ),  ( 5 ,  1 ),  ( 6 ,  2 ),  ( 7 ,  3 ))  # Puntos rojos  NUM_POINTS :  int  =  100  # Densidad de puntos de cadena azules entre dos puntos rojos chain_points :  list  =  catmull_rom_chain ( POINTS ,  NUM_POINTS )  afirmar  len ( chain_points )  ==  num_segments ( POINTS )  *  NUM_POINTS  # 400 puntos azules para este ejemplo pl . plot ( * zip ( * chain_points ),  c = "azul" )  plt . plot ( * zip ( * PUNTOS ),  c = "rojo" ,  estilo de línea = "ninguno" ,  marcador = "o" )  plt . espectáculo ()

Gráfico obtenido mediante el código de ejemplo de Python proporcionado anteriormente

Ejemplo de código en Unity C#

usando UnityEngine ; // una única curva catmull-rom public struct CatmullRomCurve { public Vector2 p0 , p1 , p2 , p3 ; alfa flotante público ;         public CatmullRomCurve ( Vector2 p0 , Vector2 p1 , Vector2 p2 , Vector2 p3 , flotante alfa ) { ( este.p0 , este.p1 , este.p2 , este.p3 ) = ( p0 , p1 , p2 , p3 ) ;​​​​​​​ este . alfa = alfa ; }                     // Evalúa un punto en el valor t dado de 0 a 1 public Vector2 GetPoint ( float t ) { // calcula nudos const float k0 = 0 ; flotador k1 = GetKnotInterval ( p0 , p1 ); flotador k2 = GetKnotInterval ( p1 , p2 ) + k1 ; flotador k3 = GetKnotInterval ( p2 , p3 ) + k2 ;                        // evalúa el punto float u = Mathf . LerpUnclamped ( k1 , k2 , t ); Vector2 A1 = Reasignar ( k0 , k1 , p0 , p1 , u ); Vector2 A2 = Reasignar ( k1 , k2 , p1 , p2 , u ); Vector2 A3 = Reasignar ( k2 , k3 , p2 , p3 , u ); Vector2 B1 = Reasignar ( k0 , k2 , A1 , A2 , u ); Vector2 B2 = Reasignar ( k1 , k3 , A2 , A3 , u ); devolver Reasignar ( k1 , k2 , B1 , B2 , u ); }                                             Reasignación estática de Vector2 ( flotante a , flotante b , Vector2 c , Vector2 d , flotante u ) { retorno Vector2 . LerpUnclamped ( c , d , ( u - a ) / ( b - a )); }                     float GetKnotInterval ( Vector2 a , Vector2 b ) { return Mathf . Pow ( Vector2 . SqrMagnitude ( a - b ), 0,5f * alfa ); } }           

usando UnityEngine ; // Dibuja un spline catmull-rom en la vista de escena, // a lo largo de los objetos secundarios de la transformación de este componente public class CatmullRomSpline : MonoBehaviour { [Range(0, 1)] public float alpha = 0.5f ; int PointCount => transformar . niñoCuenta ; int SegmentCount => PointCount - 3 ; Vector2 GetPoint ( int i ) => transformar . GetChild ( yo ). posición ;                     CatmullRomCurve GetCurve ( int i ) { devolver nuevo CatmullRomCurve ( GetPoint ( i ), GetPoint ( i + 1 ), GetPoint ( i + 2 ), GetPoint ( i + 3 ), alfa ); }         void OnDrawGizmos () { para ( int i = 0 ; i < SegmentCount ; i ++ ) DrawCurveSegment ( GetCurve ( i )); }          void DrawCurveSegment ( curva CatmullRomCurve ) { const int detalle = 32 ; Vector2 anterior = curva . p1 ;          for ( int i = 1 ; i < detalle ; i ++ ) { float t = i / ( detalle - 1f ); Vector2 pt = curva . ObtenerPunto ( t ); Artilugios . DrawLine ( anterior , pt ); anterior = pto ; } } }                      

Ejemplo de código en Unreal C++

float GetT ( flotante t , float alfa , VectorF constante y p0 , VectorF constante y p1 ) { auto d = p1 - p0 ; flotar a = d | d ; // Producto escalar float b = FMath :: Pow ( a , alpha * .5f ); retorno ( b + t ); }                                    FVector CatmullRom ( const FVector & p0 , const FVector & p1 , const FVector & p2 , const FVector & p3 , float t /* entre 0 y 1 */ , float alpha = .5f /* entre 0 y 1 */ ) { float t0 = 0,0f ; flotador t1 = ObtenerT ( t0 , alfa , p0 , p1 ); flotador t2 = ObtenerT ( t1 , alfa , p1 , p2 ); flotador t3 = ObtenerT ( t2 , alfa , p2 , p3 ); t = FMath :: Lerp ( t1 , t2 , t ); FVector A1 = ( t1 - t ) / ( t1 - t0 ) * p0 + ( t - t0 ) / ( t1 - t0 ) * p1 ; FVector A2 = ( t2 - t ) / ( t2 - t1 ) * p1 + ( t - t1 ) / ( t2 - t1 ) * p2 ; FVector A3 = ( t3 - t ) / ( t3 - t2 ) * p2 + ( t - t2 ) / ( t3 - t2 ) * p3 ; FVector B1 = ( t2 - t ) / ( t2 - t0 )                                                                                                            * A1 + ( t - t0 ) / ( t2 - t0 ) * A2 ; FVector B2 = ( t3 - t ) / ( t3 - t1 ) * A2 + ( t - t1 ) / ( t3 - t1 ) * A3 ; FVector C = ( t2 - t ) / ( t2 - t1 ) * B1 + ( t - t1 ) / ( t2 - t1 ) * B2 ; devolver C ; }                                    

Ver también

• Splines cúbicos de Hermite

Referencias

1. Catmull, Edwin ; Rom, Rafael (1974). "Una clase de splines de interpolación local". En Barnhill, Robert E.; Riesenfeld, Richard F. (eds.). Diseño Geométrico Asistido por Computadora . págs. 317–326. doi :10.1016/B978-0-12-079050-0.50020-5. ISBN 978-0-12-079050-0.
2. Barry, Phillip J.; Goldman, Ronald N. (agosto de 1988). Un algoritmo de evaluación recursivo para una clase de splines de Catmull-Rom. Actas de la 15ª Conferencia Anual sobre Gráficos por Computadora y Técnicas Interactivas, SIGGRAPH 1988. Vol. 1, núm. 22. Asociación de Maquinaria de Computación . págs. 199-204. doi :10.1145/378456.378511.
3. Yuksel, Cem; Schaefer, Scott; Keyser, John (julio de 2011). "Parametrización y aplicaciones de curvas de Catmull-Rom". Diseño asistido por ordenador . 43 (7): 747–755. CiteSeerX 10.1.1.359.9148 . doi :10.1016/j.cad.2010.08.008. 
4. Yuksel; Schaefer; Keyser, Cem; Scott; John. "Sobre la parametrización de curvas de Catmull-Rom" (PDF) .{{cite web}}: CS1 maint: multiple names: authors list (link)
5. Jen Hong, bronceado; Acharya, U. Rajendra (2014). "Modelo spline activo: una segmentación interactiva de modelo basada en formas" (PDF) . Procesamiento de señales digitales . 35 : 64–74. arXiv : 1402.6387 . doi :10.1016/j.dsp.2014.09.002. S2CID  6953844.

enlaces externos

• Curva Catmull-Rom sin cúspides ni autointersecciones: implementación en Java
• Curva Catmull-Rom sin cúspides ni autointersecciones: implementación simplificada en C++
• Splines Catmull-Rom: generación interactiva a través de Python, en un cuaderno Jupyter
• Rutas suaves usando splines Catmull-Rom: otra implementación versátil en C++ que incluye splines CR centrípetas