Bipirámide triangular

Dos tetraedros unidos por una cara

En geometría, la bipirámide triangular es el hexaedro con seis caras triangulares, construido uniendo dos tetraedros cara con cara. La misma forma también se llama bipirámide triangular ^{[1] [2]} o bipirámide trigonal . ^[3] Si estos tetraedros son regulares, todas las caras de la bipirámide triangular son equiláteras . Es un ejemplo de deltaedro , poliedro compuesto y sólido de Johnson .

Muchos poliedros están relacionados con la bipirámide triangular, como nuevas formas similares derivadas de diferentes enfoques, y el prisma triangular como su poliedro dual . Las muchas aplicaciones de la bipirámide triangular incluyen la geometría molecular de la bipirámide trigonal que describe su conjunto de átomos , una solución del problema de Thomson y la representación de sistemas de orden de color en el siglo XVIII.

Casos especiales

Como una bipirámide recta

Al igual que otras bipirámides , la bipirámide triangular se puede construir uniendo dos tetraedros cara a cara. ^[2] Estos tetraedros cubren su base triangular, de modo que el poliedro resultante tiene seis triángulos, cinco vértices y nueve aristas. ^[3] Se dice que la bipirámide triangular es recta si los tetraedros son simétricamente regulares y ambos vértices están en la línea que pasa por el centro de la base; de ​​lo contrario, es oblicua . ^{[4] [5]}

Gráfica de bipirámide triangular

Según el teorema de Steinitz , un grafo puede representarse como el esqueleto de un poliedro si es plano y grafo 3-conexo . En otras palabras, las aristas de ese grafo no se cruzan sino que solo se intersecan en el punto, y uno de los dos vértices cualesquiera deja un subgrafo conexo cuando se lo elimina. La bipirámide triangular se representa mediante un grafo con nueve aristas, construido añadiendo un vértice que se conecta a los vértices de un grafo de rueda que representa tetraedros . ^{[6] [7]}

Al igual que otras bipirámides rectas, la bipirámide triangular tiene simetría de grupo puntual tridimensional , el grupo diedro de orden doce: la apariencia de la bipirámide triangular no cambia al rotar un ángulo, dos tercios y un ángulo completo alrededor del eje de simetría (una línea que pasa por dos vértices y el centro de la base verticalmente), y tiene simetría especular con respecto a cualquier bisectriz de la base; también es simétrica al reflejarla a través de un plano horizontal. ^[8] Por lo tanto, la bipirámide triangular es transitiva por las caras o isoédrica. ^[9] ${\displaystyle D_{3\mathrm {h} }}$

Como un sólido Johnson

Bipirámide triangular con caras regulares, a lo largo de su red .

Modelo 3D de una bipirámide triangular como un sólido de Johnson

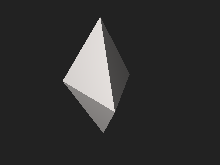
Si los tetraedros son regulares, todas las aristas de la bipirámide triangular tienen la misma longitud, formando caras triangulares equiláteras . Un poliedro con solo triángulos equiláteros como caras se llama deltaedro . Solo hay ocho deltaedros convexos diferentes, uno de los cuales es la bipirámide triangular con caras poligonales regulares . ^[1] De manera más general, el poliedro convexo en el que todas las caras son polígonos regulares es el sólido de Johnson , y cada deltaedro convexo es un sólido de Johnson. La bipirámide triangular con las caras regulares se encuentra entre los sólidos de Johnson numerados como el duodécimo sólido de Johnson . ^[10] Es un ejemplo de un poliedro compuesto , porque se construye uniendo dos tetraedros regulares . ^{[11] [12]} ${\displaystyle J_{12}}$

La superficie de una bipirámide triangular es seis veces la de cada triángulo. Su volumen se puede calcular dividiendo la bipirámide en dos tetraedros y sumando sus volúmenes. En el caso de la longitud de las aristas , es: ^[12] ${\displaystyle A}$ ${\displaystyle V}$ ${\displaystyle a}$ $${\displaystyle {\begin{aligned}A&={\frac {3{\sqrt {3}}}{2}}a^{2}&\approx 2.598a^{2},\\V&={\frac {\sqrt {2}}{6}}a^{3}&\approx 0.238a^{3}.\end{aligned}}}$$

El ángulo diedro de una bipirámide triangular se puede obtener sumando el ángulo diedro de dos tetraedros regulares. El ángulo diedro de una bipirámide triangular entre caras triangulares adyacentes es el del tetraedro regular, 70,5°. En el caso de la arista donde se unen dos tetraedros, el ángulo diedro de los triángulos adyacentes es el doble, 141,1°. ^[13]

Poliedros relacionados

El gráfico de Goldner-Harary representa la bipirámide triangular aumentada por tetraedros.

Algunos tipos de bipirámides triangulares pueden derivarse de diferentes maneras. Por ejemplo, el Kleetope de poliedros es una construcción que implica la unión de pirámides; en el caso de la bipirámide triangular, su Kleetope puede construirse a partir de una bipirámide triangular uniendo tetraedros a cada una de sus caras, cubriéndolos y reemplazándolos con otros tres triángulos; el esqueleto del poliedro resultante representa el grafo de Goldner-Harary . ^{[14] [15]} Otro tipo de bipirámide triangular es mediante el corte de todos sus vértices; este proceso se conoce como truncamiento . ^[16]

Las bipirámides son poliedros duales de prismas , en los que los vértices de las bipirámides corresponden a las caras del prisma, y ​​las aristas entre pares de vértices de una corresponden a las aristas entre pares de caras de la otra; dualidad da como resultado nuevamente el poliedro original. Por lo tanto, la bipirámide triangular es el poliedro dual del prisma triangular , y viceversa. ^{[17] [3]} El prisma triangular tiene cinco caras, nueve aristas y seis vértices, y tiene la misma simetría que la bipirámide triangular. ^[3]

Aplicaciones

La solución conocida del problema de Thomson, siendo una de ellas la bipirámide triangular.

El problema de Thomson se refiere a la configuración de energía mínima de partículas cargadas en una esfera. Una de ellas es una bipirámide triangular, que es una solución conocida para el caso de cinco electrones, al colocar los vértices de una bipirámide triangular inscritos en una esfera . ^[18] Esta solución se ve facilitada por la rigurosa computación matemática. ^[19]

En la geometría de los compuestos químicos , la geometría molecular bipiramidal trigonal puede describirse como el conjunto de átomos de la bipirámide triangular. Esta molécula tiene un elemento del grupo principal sin un par solitario activo , como se describe mediante un modelo que predice la geometría de las moléculas conocida como teoría VSEPR . ^[20] Algunos ejemplos de esta estructura son el pentafluoruro de fósforo y el pentacloruro de fósforo en fase gaseosa. ^[21]

En el estudio de la teoría del color , se utilizó la bipirámide triangular para representar el sistema tridimensional de ordenación de los colores en los colores primarios . El astrónomo alemán Tobias Mayer planteó en 1758 que cada uno de sus vértices representa los colores: el blanco y el negro son los vértices axiales superior e inferior respectivamente, mientras que el resto de los vértices son el rojo, el azul y el amarillo. ^{[22] [23]}

Referencias

1. Trigg, Charles W. (1978). "Una clase infinita de deltaedros". Revista de Matemáticas . 51 (1): 55–57. doi :10.1080/0025570X.1978.11976675. JSTOR  2689647. MR  1572246.
2. Rajwade, AR (2001). Poliedros convexos con condiciones de regularidad y el tercer problema de Hilbert. Textos y lecturas de matemáticas. Hindustan Book Agency. p. 84. doi :10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
3. King, Robert B. (1994). "Dinámica poliédrica". En Bonchev, Danail D.; Mekenyan, OG (eds.). Enfoques teóricos de grafos para la reactividad química . Springer. doi :10.1007/978-94-011-1202-4. ISBN. 978-94-011-1202-4.
4. Niu, Wenxin; Xu, Guobao (2011). "Control cristalográfico de nanocristales de metales nobles". Nano Today . 6 (3): 265–285. doi :10.1016/j.nantod.2011.04.006.
5. Alexandrov, Victor (2017). "¿Cuántas veces se puede aumentar el volumen de un poliedro convexo mediante deformaciones isométricas?". Beiträge zur Algebra und Geometrie . 58 (3): 549–554. arXiv : 1607.06604 . doi :10.1007/s13366-017-0336-8.
6. Tutte, WT (2001). Teoría de grafos. Cambridge University Press. pág. 113. ISBN 978-0-521-79489-3.
7. Sajjad, Wassid; Sardar, Muhammad S.; Pan, Xiang-Feng (2024). "Cálculo de la distancia de resistencia y el índice de Kirchhoff de la cadena de hexaedro bipirámide triangular". Matemáticas Aplicadas y Computación . 461 : 1–12. doi :10.1016/j.amc.2023.128313. S2CID  261797042.
8. Alexander, Daniel C.; Koeberlin, Geralyn M. (2014). Geometría elemental para estudiantes universitarios (6.ª ed.). Cengage Learning. pág. 403. ISBN 978-1-285-19569-8.
9. McLean, K. Robin (1990). "Mazmorras, dragones y dados". The Mathematical Gazette . 74 (469): 243–256. doi :10.2307/3619822. JSTOR  3619822. S2CID  195047512.
10. Uehara, Ryuhei (2020). Introducción al origami computacional: el mundo de la nueva geometría computacional. Springer. doi :10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. Número de identificación del sujeto  220150682.
11. Timofeenko, AV (2009). "Poliedros convexos con caras de parquet" (PDF) . Docklady Mathematics . 80 (2): 720–723. doi :10.1134/S1064562409050238.
12. Berman, Martin (1971). "Poliedros convexos de caras regulares". Revista del Instituto Franklin . 291 (5): 329–352. doi :10.1016/0016-0032(71)90071-8. MR  0290245.
13. Johnson, Norman W. (1966). "Poliedros convexos con caras regulares". Revista Canadiense de Matemáticas . 18 : 169–200. doi : 10.4153/cjm-1966-021-8 . MR  0185507. S2CID  122006114. Zbl  0132.14603.
14. Grünbaum, Branko (1967). Politopos convexos . Wiley Interscience. pág. 357.. Misma página, 2.ª ed., Graduate Texts in Mathematics 221, Springer-Verlag, 2003, ISBN 978-0-387-40409-7 . 
15. Ewald, Günter (1973). "Circuitos hamiltonianos en complejos simpliciales". Geometriae Dedicata . 2 (1): 115–125. doi :10.1007/BF00149287. S2CID  122755203.
16. Haji-Akbari, Amir; Chen, Elizabeth R.; Engel, Michael; Glotzer, Sharon C. (2013). "Empaquetamiento y autoensamblaje de bipirámides triangulares truncadas". Phys. Rev. E . 88 (1): 012127. arXiv : 1304.3147 . Código Bibliográfico :2013PhRvE..88a2127H. doi :10.1103/physreve.88.012127. PMID  23944434. S2CID  8184675..
17. Sibley, Thomas Q. (2015). Pensamiento geométrico: un estudio de geometrías. Asociación Matemática de Estados Unidos. pág. 53. ISBN 978-1-939512-08-6.
18. Sloane, NJA ; Hardin, RH; Duff, TDS; Conway, JH (1995), "Cúmulos de esferas duras de energía mínima", Geometría discreta y computacional , 14 (3): 237–259, doi : 10.1007/BF02570704 , MR  1344734, S2CID  26955765
19. Schwartz, Richard Evan (2013). "El caso de los cinco electrones del problema de Thomson". Matemáticas experimentales . 22 (2): 157–186. doi :10.1080/10586458.2013.766570. S2CID  38679186.
20. Petrucci, RH; Harwood, WS; Herring, FG (2002). Química general: principios y aplicaciones modernas (8.ª ed.). Prentice-Hall. págs. 413–414. ISBN 978-0-13-014329-7.Véase la tabla 11.1.
21. Housecroft, CE; Sharpe, AG (2004). Química inorgánica (2.ª ed.). Prentice Hall. pág. 407. ISBN 978-0-13-039913-7.
22. Kuehni, Rolf G. (2003). El espacio de color y sus divisiones: orden del color desde la antigüedad hasta la actualidad. John & Sons Wiley. pág. 53. ISBN 978-0-471-46146-3.
23. Kuehni, Rolf G. (2013). Color: Introducción a la práctica y los principios. John & Sons Wiley. pág. 198. ISBN 978-1-118-17384-8.