IEEE 754-1985 [1] es un estándar industrial histórico para representar números de punto flotante en computadoras , adoptado oficialmente en 1985 y reemplazado en 2008 por IEEE 754-2008 , y luego nuevamente en 2019 por la revisión menor IEEE 754-2019 . [2] Durante sus 23 años, fue el formato más utilizado para el cálculo de punto flotante. Se implementó en software, en forma de bibliotecas de punto flotante , y en hardware, en las instrucciones de muchas CPU y FPU . El primer circuito integrado en implementar el borrador de lo que se convertiría en IEEE 754-1985 fue el Intel 8087 .
IEEE 754-1985 representa números en binario , proporcionando definiciones para cuatro niveles de precisión, de los cuales los dos más utilizados son:
El estándar también define representaciones para el infinito positivo y negativo , un " cero negativo ", cinco excepciones para manejar resultados no válidos como la división por cero , valores especiales llamados NaN para representar esas excepciones, números desnormalizados para representar números más pequeños que los que se muestran arriba y cuatro modos de redondeo .


Los números de punto flotante en formato IEEE 754 constan de tres campos: un bit de signo , un exponente sesgado y una fracción. El siguiente ejemplo ilustra el significado de cada uno.
El número decimal 0,15625 10 representado en binario es 0,00101 2 (es decir, 1/8 + 1/32). (Los subíndices indican la base del número ). De manera análoga a la notación científica , donde los números se escriben de manera que tengan un solo dígito distinto de cero a la izquierda del punto decimal, reescribimos este número de manera que tenga un solo bit 1 a la izquierda del "punto binario". Simplemente multiplicamos por la potencia de 2 adecuada para compensar el desplazamiento de los bits a la izquierda en tres posiciones:
Ahora podemos leer la fracción y el exponente: la fracción es 0,01 2 y el exponente es −3.
Como se ilustra en las imágenes, los tres campos en la representación IEEE 754 de este número son:
IEEE 754 añade un sesgo al exponente de modo que los números se pueden comparar en muchos casos cómodamente con el mismo hardware que compara números enteros con signo en complemento a 2. Si se utiliza un exponente sesgado, el menor de dos números positivos en coma flotante resultará "menor que" el mayor siguiendo el mismo orden que para los números enteros con signo y magnitud . Si dos números en coma flotante tienen signos diferentes, la comparación de signo y magnitud también funciona con exponentes sesgados. Sin embargo, si ambos números en coma flotante con exponente sesgado son negativos, entonces el orden debe invertirse. Si el exponente se representara como, por ejemplo, un número en complemento a 2, la comparación para ver cuál de los dos números es mayor no sería tan conveniente.
Se omite el bit 1 inicial ya que todos los números excepto cero comienzan con un 1 inicial; el 1 inicial es implícito y en realidad no necesita almacenarse, lo que brinda un bit adicional de precisión "gratis".
El número cero se representa de forma especial:
Las representaciones numéricas descritas anteriormente se denominan normalizadas, lo que significa que el dígito binario inicial implícito es un 1. Para reducir la pérdida de precisión cuando se produce un desbordamiento , IEEE 754 incluye la capacidad de representar fracciones más pequeñas que las posibles en la representación normalizada, haciendo que el dígito inicial implícito sea un 0. Dichos números se denominan desnormalizados . No incluyen tantos dígitos significativos como un número normalizado, pero permiten una pérdida gradual de precisión cuando el resultado de una operación no es exactamente cero, sino que está demasiado cerca de cero para ser representado por un número normalizado.
Un número desnormalizado se representa con un exponente sesgado de todos los bits 0, lo que representa un exponente de −126 en precisión simple (no −127), o −1022 en precisión doble (no −1023). [3] Por el contrario, el exponente sesgado más pequeño que representa un número normal es 1 (ver ejemplos a continuación).
El campo de exponente sesgado se rellena con todos los bits 1 para indicar infinito o un resultado no válido de un cálculo.
El infinito positivo y negativo se representan así:
Algunas operaciones de aritmética de punto flotante no son válidas, como por ejemplo, sacar la raíz cuadrada de un número negativo. El acto de obtener un resultado no válido se denomina excepción de punto flotante. Un resultado excepcional se representa mediante un código especial llamado NaN, que significa " No es un número ". Todos los NaN en IEEE 754-1985 tienen este formato:
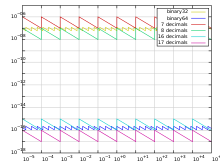
La precisión se define como la diferencia mínima entre dos representaciones de mantisa sucesivas; por lo tanto, es una función solo en la mantisa; mientras que la brecha se define como la diferencia entre dos números sucesivos. [4]
Los números de precisión simple ocupan 32 bits. En precisión simple:
Algunos ejemplos de valores de rango y brecha para exponentes dados en precisión simple:
Por ejemplo, 16 777 217 no se puede codificar como un número flotante de 32 bits, ya que se redondeará a 16 777 216. Sin embargo, todos los números enteros dentro del rango representable que sean una potencia de 2 se pueden almacenar en un número flotante de 32 bits sin redondeo.
Los números de doble precisión ocupan 64 bits. En la doble precisión:
Algunos ejemplos de valores de rango y brecha para exponentes dados en doble precisión:
La norma también recomienda que se utilicen formatos extendidos para realizar cálculos internos con una precisión mayor que la requerida para el resultado final, a fin de minimizar los errores de redondeo: la norma solo especifica los requisitos mínimos de precisión y exponente para dichos formatos. El formato extendido x87 de 80 bits es el formato extendido más comúnmente implementado que cumple con estos requisitos.
A continuación se muestran algunos ejemplos de representaciones IEEE 754 de precisión simple:
Cada combinación de bits posible es un NaN o un número con un valor único en el sistema de números reales extendido por afinidad con su orden asociado, excepto las dos combinaciones de bits para el cero negativo y el cero positivo, que a veces requieren atención especial (ver más abajo). La representación binaria tiene la propiedad especial de que, excluyendo los NaN, dos números cualesquiera pueden compararse como enteros de signo y magnitud ( se aplican problemas de endianness ). Al comparar como enteros de complemento a 2 : si los bits de signo difieren, el número negativo precede al número positivo, por lo que el complemento a 2 da el resultado correcto (excepto que el cero negativo y el cero positivo deben considerarse iguales). Si ambos valores son positivos, la comparación de complemento a 2 da nuevamente el resultado correcto. De lo contrario (dos números negativos), el orden FP correcto es el opuesto al orden de complemento a 2.
Los errores de redondeo inherentes a los cálculos de punto flotante pueden limitar el uso de comparaciones para verificar la igualdad exacta de los resultados. Elegir un rango aceptable es un tema complejo. Una técnica común es usar un valor de comparación épsilon para realizar comparaciones aproximadas. [6] Dependiendo de qué tan indulgentes sean las comparaciones, los valores comunes incluyen 1e-6o 1e-5para precisión simple y 1e-14para precisión doble. [7] [8] Otra técnica común es ULP, que verifica cuál es la diferencia en los últimos dígitos de lugar, verificando efectivamente cuántos pasos de distancia hay entre los dos valores. [9]
Aunque el cero negativo y el cero positivo se consideran generalmente iguales a efectos de comparación, algunos operadores relacionales de lenguajes de programación y construcciones similares los tratan como distintos. Según la Especificación del lenguaje Java , [10] los operadores de comparación e igualdad los tratan como iguales, pero y los distinguen (oficialmente a partir de la versión 1.1 de Java, pero en realidad con la 1.1.1), al igual que los métodos de comparación , e incluso de clases y .Math.min()Math.max()equals()compareTo()compare()FloatDouble
El estándar IEEE tiene cuatro modos de redondeo diferentes; el primero es el predeterminado; los demás se denominan redondeos dirigidos .
El estándar IEEE emplea (y extiende) el sistema de números reales extendido de forma afín , con infinitos positivos y negativos separados. Durante la redacción, hubo una propuesta para que el estándar incorporara el sistema de números reales extendido de forma proyectiva , con un único infinito sin signo, proporcionando a los programadores una opción de selección de modo. Sin embargo, con el fin de reducir la complejidad del estándar final, se eliminó el modo proyectivo. Los coprocesadores de punto flotante Intel 8087 e Intel 80287 admiten este modo proyectivo. [11] [12] [13]
Se deben proporcionar las siguientes funciones:
NaNpara cualquier x (incluido NaN).copysign(x,y)devuelve x con el signo de y, por lo que es abs(x)igual a copysign(x,1.0). Esta es una de las pocas operaciones que opera sobre un NaN de una manera similar a la aritmética. La función copysignes nueva en el estándar C99.scalb(y, N)logb(x)finite(x)un predicado para "x es un valor finito", equivalente a −Inf < x < Infisnan(x)un predicado para "x es un NaN", equivalente a "x ≠ x"x <> y( x .LG. yen Fortran ), que resulta tener un comportamiento diferente a NOT(x = y)( x .NE. yen Fortran, x != yen C ) [14] debido a NaN.unordered(x, y)es verdadero cuando "x no está ordenado con y", es decir, x o y es un NaN.class(x)nextafter(x,y)devuelve el siguiente valor representable desde x en la dirección hacia yEn 1976, Intel estaba empezando a desarrollar un coprocesador de punto flotante . [15] [16] Intel esperaba poder vender un chip que contuviera buenas implementaciones de todas las operaciones que se encuentran en las muy variadas bibliotecas de software matemático. [15] [17]
John Palmer, quien dirigió el proyecto, creía que el esfuerzo debería estar respaldado por un estándar que unificara las operaciones de punto flotante en procesadores dispares. Se puso en contacto con William Kahan de la Universidad de California , que había ayudado a mejorar la precisión de las calculadoras de Hewlett-Packard . Kahan sugirió que Intel utilizara el punto flotante del VAX de Digital Equipment Corporation (DEC). El primer VAX, el VAX-11/780, acababa de salir a finales de 1977, y su punto flotante era muy valorado. Sin embargo, buscando comercializar su chip en el mercado más amplio posible, Intel quería el mejor punto flotante posible, y Kahan pasó a redactar las especificaciones. [15] Kahan inicialmente recomendó que la base del punto flotante fuera decimal [18] [¿ fuente poco fiable? ] pero el diseño de hardware del coprocesador estaba demasiado avanzado para hacer ese cambio.
El trabajo dentro de Intel preocupó a otros proveedores, que establecieron un esfuerzo de estandarización para garantizar un "campo de juego nivelado". Kahan asistió a la segunda reunión del grupo de trabajo de estándares IEEE 754, celebrada en noviembre de 1977. Posteriormente recibió permiso de Intel para presentar un borrador de propuesta basado en su trabajo para su coprocesador; se le permitió explicar los detalles del formato y su fundamento, pero nada relacionado con la arquitectura de implementación de Intel. El borrador fue coescrito con Jerome Coonen y Harold Stone , y fue conocido inicialmente como la "propuesta Kahan-Coonen-Stone" o "formato KCS". [15] [16] [17] [19]
Como un exponente de 8 bits no era lo suficientemente amplio para algunas operaciones deseadas para números de doble precisión, por ejemplo, para almacenar el producto de dos números de 32 bits, [20] tanto la propuesta de Kahan como una contrapropuesta de DEC utilizaron 11 bits, como el formato de punto flotante de 60 bits probado en el tiempo del CDC 6600 de 1965. [16] [19] [21] La propuesta de Kahan también preveía infinitos, que son útiles cuando se trata de condiciones de división por cero; valores que no son números, que son útiles cuando se trata de operaciones no válidas; números desnormalizados , que ayudan a mitigar los problemas causados por el desbordamiento insuficiente; [19] [22] [23] y un sesgo de exponente mejor equilibrado , que puede ayudar a evitar el desbordamiento y el desbordamiento insuficiente al tomar el recíproco de un número. [24] [25]
Incluso antes de su aprobación, el proyecto de norma ya había sido implementado por varios fabricantes. [26] [27] El Intel 8087, que se anunció en 1980, fue el primer chip en implementar el proyecto de norma.

En 1980, ya se había lanzado el chip Intel 8087 , [28] pero DEC siguió oponiéndose, en particular a los números desnormalizados, por cuestiones de rendimiento y porque le daría a DEC una ventaja competitiva para estandarizar el formato de DEC.
Las discusiones sobre el subdesbordamiento gradual duraron hasta 1981, cuando un experto contratado por la DEC para evaluarlo se puso del lado de los disidentes. La DEC encargó que se realizara el estudio para demostrar que el subdesbordamiento gradual era una mala idea, pero el estudio concluyó lo contrario y la DEC cedió. En 1985, la norma fue ratificada, pero ya se había convertido en la norma de facto un año antes, implementada por muchos fabricantes. [16] [19] [5]