Pista de Hayashi

Relación luminosidad-temperatura en las estrellas

Trayectorias de evolución estelar (líneas azules) para la presecuencia principal. Las curvas casi verticales son las trayectorias de Hayashi.
Las estrellas de baja masa tienen trayectorias de evolución casi verticales hasta que llegan a la secuencia principal. En el caso de las estrellas más masivas, la trayectoria de Hayashi se curva hacia la izquierda y se convierte en la trayectoria de Henyey . Incluso estrellas más masivas nacen directamente en la trayectoria de Henyey.
El final (punto más a la izquierda) de cada trayectoria está marcado con la masa de la estrella en masas solares ( M ☉ ), y representa su posición en la secuencia principal. Las curvas rojas marcadas en años son isócronas en las edades dadas. En otras palabras, las estrellas de 10^{Los niños de 5} años se encuentran a lo largo de la curva marcada con 10⁵ , y lo mismo para las otras 3 isócronas.

La trayectoria de Hayashi es una relación de luminosidad-temperatura que siguen las estrellas infantiles de menos de 3  M☉ en la fase de presecuencia principal (fase PMS) de la evolución estelar. Recibe su nombre del astrofísico japonés Chushiro Hayashi . En el diagrama de Hertzsprung-Russell , que representa gráficamente la luminosidad frente a la temperatura, la trayectoria es una curva casi vertical. Después de que una protoestrella termina su fase de contracción rápida y se convierte en una estrella T Tauri , es extremadamente luminosa. La estrella continúa contrayéndose, pero mucho más lentamente. Mientras se contrae lentamente, la estrella sigue la trayectoria de Hayashi hacia abajo, volviéndose varias veces menos luminosa pero manteniéndose aproximadamente a la misma temperatura superficial, hasta que se desarrolla una zona radiativa , momento en el que la estrella comienza a seguir la trayectoria de Henyey , o comienza la fusión nuclear, marcando su entrada en la secuencia principal .

La forma y la posición de la trayectoria de Hayashi en el diagrama de Hertzsprung-Russell dependen de la masa y la composición química de la estrella. En el caso de las estrellas de masa solar, la trayectoria se encuentra a una temperatura de aproximadamente 4000 K. Las estrellas en la trayectoria son casi completamente convectivas y su opacidad está dominada por iones de hidrógeno. Las estrellas de menos de 0,5  M _☉ son completamente convectivas incluso en la secuencia principal, pero su opacidad comienza a estar dominada por la ley de opacidad de Kramers después de que comienza la fusión nuclear, lo que las aleja de la trayectoria de Hayashi. Las estrellas entre 0,5 y 3  M _☉ desarrollan una zona radiativa antes de alcanzar la secuencia principal. Las estrellas entre 3 y 10  M _☉ son completamente radiativas al comienzo de la presecuencia principal. Incluso las estrellas más pesadas nacen en la secuencia principal, sin evolución de PMS. ^[1]

Al final de la vida de una estrella de masa baja o intermedia, la estrella sigue un recorrido análogo al de Hayashi, pero a la inversa: aumenta su luminosidad, se expande y permanece aproximadamente a la misma temperatura, hasta convertirse finalmente en una gigante roja .

Historia

En 1961, el profesor Chushiro Hayashi publicó dos artículos ^{[2] [3]} que condujeron al concepto de presecuencia principal y forman la base de la comprensión moderna de la evolución estelar temprana. Hayashi se dio cuenta de que el modelo existente, en el que se supone que las estrellas están en equilibrio radiativo sin una zona de convección sustancial, no puede explicar la forma de la rama de gigante roja . ^[4] Por lo tanto, reemplazó el modelo incluyendo los efectos de las zonas de convección gruesas en el interior de una estrella.

Unos años antes, Osterbrock había propuesto zonas de convección profunda con convección eficiente, analizándolas utilizando la opacidad de los iones H (la fuente de opacidad dominante en atmósferas frías) a temperaturas inferiores a 5000 K. Sin embargo, los primeros modelos numéricos de estrellas similares al Sol no siguieron este trabajo y continuaron suponiendo un equilibrio radiativo. ^[1]

En sus artículos de 1961, Hayashi demostró que la envoltura convectiva de una estrella está determinada por: donde E no tiene unidades, y no la energía . Modelando las estrellas como politropos con índice 3/2 —en otras palabras, suponiendo que siguen una relación presión-densidad de — encontró que E = 45 es el máximo para una estrella cuasiestática . Si una estrella no se está contrayendo rápidamente, E = 45 define una curva en el diagrama HR, a la derecha de la cual la estrella no puede existir. Luego calculó las trayectorias evolutivas y las isócronas (distribuciones de luminosidad-temperatura de las estrellas a una edad dada) para una variedad de masas estelares y observó que NGC2264 , un cúmulo de estrellas muy joven, se ajusta bien a las isócronas. En particular, calculó edades mucho más bajas para las estrellas de tipo solar en NGC2264 y predijo que estas estrellas eran estrellas T Tauri en rápida contracción . $${\displaystyle E=4\pi G^{3/2}\left({\frac {\mu H}{k}}\right)^{5/2}{\frac {M^{1/2}R^{3/2}P}{T^{5/2}}}}$$ ${\displaystyle P=K\rho ^{5/3}}$

En 1962, Hayashi publicó una reseña de 183 páginas sobre la evolución estelar. En ella, analizaba la evolución de las estrellas nacidas en la región prohibida. Estas estrellas se contraen rápidamente debido a la gravedad antes de asentarse en un estado cuasiestático, totalmente convectivo, en las trayectorias de Hayashi.

En 1965, los modelos numéricos de Iben y Ezer & Cameron simularon de forma realista la evolución anterior a la secuencia principal, incluida la trayectoria de Henyey que siguen las estrellas después de abandonar la trayectoria de Hayashi. Estas trayectorias estándar de PMS todavía se pueden encontrar en los libros de texto sobre evolución estelar.

Zona prohibida

La zona prohibida es la región del diagrama HR a la derecha de la trayectoria de Hayashi donde ninguna estrella puede estar en equilibrio hidrostático , incluso aquellas que son parcial o totalmente radiactivas. Las protoestrellas recién nacidas comienzan en esta zona, pero no están en equilibrio hidrostático y se moverán rápidamente hacia la trayectoria de Hayashi.

Como las estrellas emiten luz a través de la radiación del cuerpo negro , la potencia por unidad de superficie que emiten viene dada por la ley de Stefan-Boltzmann : Por lo tanto, la luminosidad de la estrella viene dada por: $${\displaystyle j^{\star }=\sigma T^{4}}$$ $${\displaystyle L=4\pi R^{2}\sigma T^{4}}$$

Para un valor L dado , una temperatura más baja implica un radio mayor, y viceversa. Por lo tanto, la trayectoria de Hayashi separa el diagrama HR en dos regiones: la región permitida a la izquierda, con temperaturas altas y radios más pequeños para cada luminosidad, y la región prohibida a la derecha, con temperaturas más bajas y radios correspondientemente más altos. El límite de Hayashi puede referirse tanto al límite inferior de la temperatura como al límite superior del radio definido por la trayectoria de Hayashi.

La región de la derecha está prohibida porque se puede demostrar que una estrella en la región debe tener un gradiente de temperatura de: donde para un gas ideal monoatómico que experimenta expansión o contracción adiabática . Por lo tanto, un gradiente de temperatura mayor que 0,4 se denomina superadiabático. $${\displaystyle {\frac {d\ln T}{d\ln P}}>0.4}$$ ${\displaystyle {\frac {d\ln T}{d\ln P}}=0.4}$

Consideremos una estrella con un gradiente superadiabático. Imaginemos una parcela de gas que comienza en la posición radial r , pero se mueve hacia arriba hasta r + dr en un tiempo suficientemente corto como para intercambiar calor despreciable con sus alrededores; en otras palabras, el proceso es adiabático. La presión de los alrededores, así como la de la parcela, disminuyen en cierta cantidad dP . La temperatura de la parcela cambia en . La temperatura de los alrededores también disminuye, pero en una cantidad dT′ que es mayor que dT . Por lo tanto, la parcela termina siendo más caliente que sus alrededores. Dado que la ley de los gases ideales puede escribirse como , una temperatura más alta implica una densidad más baja a la misma presión. Por lo tanto, la parcela también es menos densa que sus alrededores. Esto hará que se eleve aún más, y la parcela se volverá incluso menos densa que sus nuevos alrededores. ${\textstyle dT=0.4{\frac {T}{P}}dP}$ ${\displaystyle P={\frac {\rho RT}{\mu }}}$

Es evidente que esta situación no es estable. De hecho, un gradiente superadiabático provoca convección . La convección tiende a reducir el gradiente de temperatura porque la porción ascendente de gas acabará dispersándose, vertiendo su exceso de energía térmica y cinética en su entorno y calentándolo. En las estrellas, se sabe que el proceso de convección es muy eficiente, con una velocidad típica que solo supera el gradiente adiabático en 1 parte en 10 millones. ^[5] ${\displaystyle {\frac {d\ln T}{d\ln P}}}$

Si una estrella se sitúa en la zona prohibida, con un gradiente de temperatura mucho mayor que 0,4, experimentará una convección rápida que reducirá el gradiente. Como esta convección cambiará drásticamente la distribución de presión y temperatura de la estrella, la estrella no estará en equilibrio hidrostático y se contraerá hasta alcanzarlo.

Una estrella situada muy a la izquierda de la trayectoria de Hayashi tiene un gradiente de temperatura menor que el adiabático. Esto significa que si una porción de gas se eleva un poquito, será más densa que sus alrededores y se hundirá de nuevo hacia el lugar de donde vino. Por lo tanto, no se produce convección y casi toda la energía emitida se transmite por radiación.

Formación de estrellas

Las estrellas se forman cuando pequeñas regiones de una nube molecular gigante colapsan bajo su propia gravedad, convirtiéndose en protoestrellas . El colapso libera energía gravitatoria, que calienta la protoestrella. Este proceso ocurre en la escala de tiempo de caída libre , que es de aproximadamente 100.000 años para las protoestrellas de masa solar, y termina cuando la protoestrella alcanza aproximadamente 4000 K. Esto se conoce como el límite de Hayashi, y en este punto, la protoestrella está en la trayectoria de Hayashi. En este punto, se conocen como estrellas T Tauri y continúan contrayéndose, pero mucho más lentamente. A medida que se contraen, disminuyen en luminosidad porque hay menos área de superficie disponible para emitir luz. La trayectoria de Hayashi da el cambio resultante en la temperatura, que será mínimo en comparación con el cambio en la luminosidad porque la trayectoria de Hayashi es casi vertical. En otras palabras, en el diagrama HR, una estrella T Tauri comienza en la trayectoria de Hayashi con una alta luminosidad y se mueve hacia abajo a lo largo de la trayectoria a medida que pasa el tiempo.

La trayectoria de Hayashi describe una estrella completamente convectiva . Esta es una buena aproximación para estrellas muy jóvenes de presecuencia principal porque aún son frías y altamente opacas , de modo que el transporte radiativo es insuficiente para llevarse la energía generada y debe ocurrir convección. Las estrellas menos masivas que 0,5  M _☉ permanecen completamente convectivas y, por lo tanto, permanecen en la trayectoria de Hayashi, a lo largo de su etapa de presecuencia principal, uniéndose a la secuencia principal en la parte inferior de la trayectoria de Hayashi. Las estrellas más pesadas que 0,5  M _☉ tienen temperaturas interiores más altas, lo que disminuye su opacidad central y permite que la radiación se lleve grandes cantidades de energía. Esto permite que se desarrolle una zona radiativa alrededor del núcleo de la estrella. La estrella ya no está en la trayectoria de Hayashi y experimenta un período de aumento rápido de temperatura a luminosidad casi constante. Esto se llama trayectoria de Henyey y termina cuando las temperaturas son lo suficientemente altas como para encender la fusión de hidrógeno en el núcleo. La estrella está entonces en la secuencia principal .

Las estrellas de menor masa siguen la trayectoria de Hayashi hasta que esta se cruza con la secuencia principal, momento en el que comienza la fusión de hidrógeno y la estrella sigue la secuencia principal. Incluso las "estrellas" de menor masa nunca alcanzan las condiciones necesarias para fusionar hidrógeno y convertirse en enanas marrones .

Derivación

La forma y posición exactas de la trayectoria de Hayashi sólo se pueden calcular numéricamente mediante modelos informáticos. No obstante, podemos elaborar un argumento analítico extremadamente rudimentario que captura la mayoría de las propiedades de la trayectoria. La siguiente derivación sigue vagamente la de Kippenhahn, Weigert y Weiss en Stellar Structure and Evolution . ^[5]

En nuestro modelo simple, se supone que una estrella consta de un interior totalmente convectivo dentro de una atmósfera totalmente radiactiva.

Se supone que el interior convectivo es un gas monoatómico ideal con un gradiente de temperatura perfectamente adiabático: $${\displaystyle {\frac {d\ln {T}}{d\ln {P}}}=0.4}$$

Esta cantidad a veces se denomina . Por lo tanto, la siguiente ecuación adiabática es válida para todo el interior: donde es la gamma adiabática , que es 5/3 para un gas monoatómico ideal. La ley de los gases ideales dice: ${\displaystyle \nabla }$ $${\displaystyle P^{1-\gamma }T^{\gamma }=C}$$ ${\displaystyle \gamma }$ $${\displaystyle {\begin{aligned}P&=NkT/V\\[1ex]&={\frac {\rho kT}{\mu _{H}}}\\[1ex]&=\left({\frac {k\rho }{\mu _{H}}}\right)^{\gamma }C\end{aligned}}}$$

donde es el peso molecular por partícula y H es (con una aproximación muy buena) la masa de un átomo de hidrógeno. Esta ecuación representa un politropo de índice 1,5, ya que un politropo se define por , donde n=1,5 es el índice politrópico. Aplicando la ecuación al centro de la estrella se obtiene: ${\displaystyle \mu _{H}}$ ${\displaystyle P=K\rho ^{1+1/n}}$ $${\displaystyle P_{c}=\left({\frac {k\rho _{c}}{\mu H}}\right)^{\gamma }C.}$$

Podemos resolver para C: $${\displaystyle C=\left({\frac {\mu _{H}}{\rho _{c}k}}\right)^{\gamma }P_{c}}$$

Pero para cualquier politropo, y . son todas constantes independientes de la presión y la densidad, y la densidad promedio se define como . Sustituyendo estas 2 ecuaciones en la ecuación para C , tenemos: donde se han ignorado todas las constantes multiplicativas. Recordemos que nuestra definición original de C era: ${\displaystyle P_{c}=W_{n}{\frac {GM^{2}}{R^{4}}}}$ ${\displaystyle \rho _{c}=K_{n}\rho _{\text{avg}}}$ ${\displaystyle W_{n},K_{n}}$ ${\displaystyle \rho _{\text{avg}}\equiv {\frac {M}{{\frac {4}{3}}\pi R^{3}}}}$ $${\displaystyle C\sim M^{2-\gamma }R^{3\gamma -4}}$$ $${\displaystyle P^{1-\gamma }T^{\gamma }=C}$$

Tenemos entonces, para cualquier estrella de masa M y radio R: $${\displaystyle P^{1-\gamma }T^{\gamma }\sim M^{2-\gamma }R^{3\gamma -4}}$$

Necesitamos otra relación entre P , T , M y R para eliminar P . Esta relación provendrá del modelo atmosférico.

Se supone que la atmósfera es delgada, con una opacidad media k . La opacidad se define como la profundidad óptica dividida por la densidad. Por lo tanto, por definición, la profundidad óptica de la superficie estelar, también llamada fotosfera , es: donde R es el radio estelar, también conocido como la posición de la fotosfera. La presión en la superficie es: $${\displaystyle {\frac {d\tau }{dr}}=k\rho }$$ $${\displaystyle \tau =\int _{R}^{\infty }k\rho \,dr=k\int _{R}^{\infty }\rho \,dr}$$ $${\displaystyle {\begin{aligned}P_{0}&=\int _{R}^{\infty }g\rho \,dr\\&={\frac {GM}{R^{2}}}\int _{R}^{\infty }\rho \,dr\\&={\frac {GM\tau }{kR^{2}}}\end{aligned}}}$$

La profundidad óptica en la fotosfera resulta ser . Por definición, la temperatura de la fotosfera es donde la temperatura efectiva viene dada por . Por lo tanto, la presión es: ${\displaystyle \tau =2/3}$ ${\displaystyle T=T_{\text{eff}}}$ ${\displaystyle L=4\pi R^{2}T_{\text{eff}}^{4}}$ $${\displaystyle P_{0}={\frac {GM}{R^{2}}}{\frac {2}{3k}}}$$

Podemos aproximar la opacidad a: donde a = 1 , b = 3. Si introducimos esto en la ecuación de presión, obtenemos: $${\displaystyle k=k_{0}P^{a}T^{b}}$$ $${\displaystyle P_{0}\propto \left({\frac {M}{R^{2}T_{\text{eff}}^{b}}}\right)^{\frac {1}{a+1}}}$$

Por último, debemos eliminar R e introducir L , la luminosidad. Esto se puede hacer con la ecuación: $${\displaystyle L=4\pi R^{2}\sigma T_{\text{eff}}^{4}}$$

Ahora las ecuaciones 1 y 2 se pueden combinar estableciendo y en la ecuación 1, y luego eliminando . R se puede eliminar usando la ecuación 3. Después de un poco de álgebra y después de establecer , obtenemos: donde ${\displaystyle T=T_{\text{eff}}}$ ${\displaystyle P=P_{0}}$ ${\displaystyle P_{0}}$ ${\displaystyle \gamma =5/3}$ $${\displaystyle \ln {T_{\text{eff}}}=A\ln {L}+B\ln {M}+\mathrm {const} }$$ $${\displaystyle {\begin{aligned}A&={\frac {0.75a-0.25}{5.5a+b+1.5}}\\B&={\frac {0.5a+1.5}{5.5a+b+1.5}}\end{aligned}}}$$

En atmósferas estelares frías ( T < 5000 K ) como las de las estrellas recién nacidas, la fuente dominante de opacidad es el ion H ^- , para el cual y , obtenemos y . ${\displaystyle a\approx 1}$ ${\displaystyle b\approx 3}$ ${\displaystyle A=0.05}$ ${\displaystyle B=0.2}$

Como A es mucho más pequeño que 1, la trayectoria de Hayashi es extremadamente empinada: si la luminosidad cambia en un factor de 2, la temperatura solo cambia en un 4 por ciento. El hecho de que B sea positivo indica que la trayectoria de Hayashi se desplaza hacia la izquierda en el diagrama HR, hacia temperaturas más altas, a medida que aumenta la masa. Aunque este modelo es extremadamente rudimentario, estas observaciones cualitativas están totalmente respaldadas por simulaciones numéricas.

A altas temperaturas, la opacidad de la atmósfera comienza a estar dominada por la ley de opacidad de Kramers en lugar del ion H, con a = 1 y b = −4,5. En ese caso, A = 0,2 en nuestro modelo crudo, mucho más alto que 0,05, y la estrella ya no está en la trayectoria de Hayashi.

En Stellar Interiors , Hansen, Kawaler y Trimble realizan una derivación similar sin descuidar las constantes multiplicativas ^[6] y llegaron a: donde es el peso molecular por partícula. Los autores señalan que el coeficiente de 2600 K es demasiado bajo (debería rondar los 4000 K), pero esta ecuación muestra, no obstante, que la temperatura es casi independiente de la luminosidad. $${\displaystyle T_{\text{eff}}=\left(\mathrm {2600K} \right)\mu ^{13/51}\left({\frac {M}{M_{\odot }}}\right)^{7/51}\left({\frac {L}{L_{\odot }}}\right)^{1/102}}$$ ${\displaystyle \mu }$

Resultados numéricos

Pistas de Hayashi de una  estrella de 0,8 M _{☉ con fracción de masa de helio de 0,245, para 3 metalicidades diferentes}

El diagrama que aparece en la parte superior de este artículo muestra trayectorias de evolución estelar calculadas numéricamente para distintas masas. Las porciones verticales de cada trayectoria son la trayectoria de Hayashi. Los puntos finales de cada trayectoria se encuentran en la secuencia principal. Los segmentos horizontales de las estrellas de mayor masa muestran la trayectoria de Henyey .

Es aproximadamente cierto que: $${\displaystyle {\frac {\partial \ln {T_{\text{eff}}}}{\partial \ln {M}}}\approx 0.1.}$$

El diagrama de la derecha muestra cómo cambian las trayectorias de Hayashi con los cambios en la composición química. Z es la metalicidad de la estrella , la fracción de masa que no se explica por el hidrógeno o el helio. Para cualquier fracción de masa de hidrógeno dada, aumentar Z conduce a un aumento del peso molecular. La dependencia de la temperatura con el peso molecular es extremadamente pronunciada: es de aproximadamente Disminuir Z en un factor de 10 desplaza la trayectoria hacia la derecha, cambiando aproximadamente 0,05. $${\displaystyle {\frac {\partial \ln {T_{\text{eff}}}}{\partial \ln {\mu }}}\approx -26.}$$ ${\displaystyle \ln {T_{\text{eff}}}}$

La composición química afecta la trayectoria de Hayashi de varias maneras. La trayectoria depende en gran medida de la opacidad de la atmósfera, y esta opacidad está dominada por el ion H-. La abundancia del ion H- es proporcional a la densidad de electrones libres, que, a su vez, es mayor si hay más metales porque los metales son más fáciles de ionizar que el hidrógeno o el helio.

Estado de observación

El cúmulo estelar joven NGC 2264, con una gran cantidad de estrellas T Tauri que se contraen hacia la secuencia principal. La línea continua representa la secuencia principal, mientras que las dos líneas superiores son las 10^6,5 años (superior) y 10Isócronas ^{de 6,7 años (inferiores).}

La evidencia observacional de la trayectoria de Hayashi proviene de los gráficos de color-magnitud (el equivalente observacional de los diagramas HR) de cúmulos estelares jóvenes. ^[1] En el caso de Hayashi, NGC 2264 proporcionó la primera evidencia de una población de estrellas en contracción. En 2012, los datos de NGC 2264 se volvieron a analizar para tener en cuenta el enrojecimiento y la extinción del polvo. El gráfico de color-magnitud resultante se muestra a la derecha.

En el diagrama superior, las isócronas son curvas a lo largo de las cuales se espera que se encuentren las estrellas de una cierta edad, suponiendo que todas las estrellas evolucionan a lo largo de la trayectoria de Hayashi. Una isócrona se crea tomando estrellas de todas las masas concebibles, haciéndolas evolucionar hacia adelante hasta la misma edad y trazándolas todas en el diagrama de color-magnitud. La mayoría de las estrellas en NGC 2264 ya están en la secuencia principal (línea negra), pero una población sustancial se encuentra entre las isócronas durante 3,2 millones y 5 millones de años, lo que indica que el cúmulo tiene entre 3,2 y 5 millones de años y una gran población de estrellas T Tauri todavía está en sus respectivas trayectorias de Hayashi. Se han obtenido resultados similares para NGC 6530, IC 5146 y NGC 6611. ^[1]

Las curvas numeradas muestran las trayectorias de Hayashi de estrellas de esa masa (en masas solares). Los círculos pequeños representan datos de observación de estrellas T Tauri. La curva en negrita a la derecha es la línea de nacimiento, por encima de la cual existen pocas estrellas.

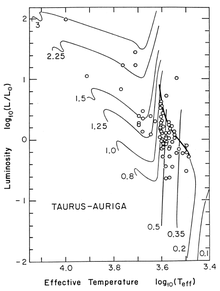
El diagrama inferior muestra las trayectorias de Hayashi para varias masas, junto con las observaciones de T Tauri recopiladas de una variedad de fuentes. Observe la curva en negrita a la derecha, que representa una línea de nacimiento estelar . Aunque algunas trayectorias de Hayashi teóricamente se extienden por encima de la línea de nacimiento, pocas estrellas están por encima de ella. En efecto, las estrellas "nacen" en la línea de nacimiento antes de evolucionar hacia abajo a lo largo de sus respectivas trayectorias de Hayashi.

La línea de nacimiento existe porque las estrellas se formaron a partir de núcleos superdensos de nubes moleculares gigantes de adentro hacia afuera. ^[4] Es decir, una pequeña región central primero colapsa sobre sí misma mientras que la capa exterior todavía está casi estática. Luego, la envoltura exterior se acrecienta sobre la protoestrella central. Antes de que finalice la acreción, la protoestrella queda oculta a la vista y, por lo tanto, no se representa en el diagrama de color-magnitud. Cuando la envoltura termina de acrecentarse, la estrella se revela y aparece en la línea de nacimiento.

Véase también

• Las estrellas históricamente más brillantes
• Lista de las estrellas más brillantes
• Lista de las estrellas más luminosas
• Lista de estrellas brillantes más cercanas
• Línea de nacimiento estelar
• Isócrona estelar

Referencias

1. Palla, Francesco (2012). "1961–2011: Cincuenta años de huellas de Hayashi". First Stars IV: From Hayashi to the Future . Actas de la conferencia AIP. Vol. 1480. págs. 22–29. Código Bibliográfico :2012AIPC.1480...22P. doi :10.1063/1.4754323. ISSN  0094-243X.
2. Hayashi, Chushiro (1961). "Evolución estelar en las primeras fases de la contracción gravitacional". Publicaciones de la Sociedad Astronómica de Japón . 13 : 450–452. Código Bibliográfico :1961PASJ...13..450H.
3. Hayashi, Chushiro (1961). "La envoltura exterior de las estrellas gigantes con zona de convección superficial". Publicaciones de la Sociedad Astronómica de Japón . 13 : 442–449. Código Bibliográfico :1961PASJ...13..442H.
4. Stahler, Steven W. (1988). "Entendiendo las estrellas jóvenes - Una historia". Publicaciones de la Sociedad Astronómica del Pacífico . 100 : 1474. Bibcode :1988PASP..100.1474S. doi :10.1086/132352. ISSN  0004-6280. S2CID  121344832.
5. Estructura estelar y evolución . Nueva York: Springer. 2012. págs. 271–282. ISBN 978-3-642-30255-8.
6. Hansen, Carl J.; Kawaler, Steven D.; Trimble, Virginia (2004). Interiores estelares: principios físicos, estructura y evolución . Nueva York: Springer. pp. 367–374. ISBN. 978-0-387-20089-7.