Transformación directa de cuadratura cero

Tensor que rota el marco de referencia para simplificar el análisis

La transformación de cuadratura directa cero ( DQZ o DQ0 ^[1] o DQO ^[2] , a veces en minúscula) o transformación de cuadratura directa cero ^[3] ( 0DQ u ODQ , a veces en minúscula) es un tensor que rota el marco de referencia de un vector de tres elementos o una matriz de tres por tres elementos en un esfuerzo por simplificar el análisis. La transformación DQZ es el producto de la transformación de Clarke y la transformación de Park, propuesta por primera vez en 1929 por Robert H. Park . ^[4]

La transformada DQZ se utiliza a menudo en el contexto de la ingeniería eléctrica con circuitos trifásicos . La transformada se puede utilizar para rotar los marcos de referencia de las formas de onda de CA de modo que se conviertan en señales de CC . A continuación, se pueden realizar cálculos simplificados sobre estas magnitudes de CC antes de realizar la transformada inversa para recuperar los resultados reales de CA trifásica. Como ejemplo, la transformada DQZ se utiliza a menudo para simplificar el análisis de máquinas síncronas trifásicas o para simplificar los cálculos para el control de inversores trifásicos. En el análisis de máquinas síncronas trifásicas, la transformación transfiere magnitudes trifásicas del estator y del rotor a un único marco de referencia giratorio para eliminar el efecto de las inductancias variables en el tiempo y transformar el sistema en un sistema lineal invariante en el tiempo.

Introducción

La transformación DQZ está formada por las matrices de transformación de Park y Clarke. La transformación de Clarke (nombrada en honor a Edith Clarke ) convierte vectores en el marco de referencia ABC al marco de referencia XYZ (también llamado αβγ ). El valor principal de la transformación de Clarke es aislar la parte del vector referenciado por ABC que es común a los tres componentes del vector; aísla el componente de modo común (es decir, el componente Z ). La matriz de transformación de Clarke invariante a la potencia, de escala uniforme y de giro a la derecha es

${\displaystyle K_{C}={\sqrt {\frac {2}{3}}}\cdot {\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}}$.

Para convertir un vector de columna referenciado ABC al marco de referencia XYZ , el vector debe multiplicarse previamente por la matriz de transformación de Clarke:

${\displaystyle {\vec {u}}_{XYZ}=K_{C}\cdot {\vec {u}}_{ABC}}$.

Y, para volver a convertir desde un vector de columna referenciado XYZ al marco de referencia ABC , el vector debe premultiplicarse por la matriz de transformación de Clarke inversa:

${\displaystyle {\vec {u}}_{ABC}=K_{C}^{-1}\cdot {\vec {u}}_{XYZ}}$.

La transformada de Park (nombrada en honor a Robert H. Park ) convierte vectores en el marco de referencia XYZ al marco de referencia DQZ . El valor principal de la transformada de Park es rotar el marco de referencia de un vector a una frecuencia arbitraria. La transformada de Park desplaza el espectro de frecuencia de la señal de modo que la frecuencia arbitraria ahora aparece como "dc" y la antigua dc aparece como el negativo de la frecuencia arbitraria. La matriz de la transformación de Park es

${\displaystyle K_{P}={\begin{bmatrix}\cos {\left(\theta \right)}&\sin {\left(\theta \right)}&0\\-\sin {\left(\theta \right)}&\cos {\left(\theta \right)}&0\\0&0&1\end{bmatrix}}}$,

donde θ es el ángulo instantáneo de una frecuencia ω arbitraria . Para convertir un vector referenciado XYZ al marco de referencia DQZ , la señal del vector de columna debe ser premultiplicada por la matriz de transformación de Park:

${\displaystyle u_{DQZ}=K_{P}\cdot u_{XYZ}}$.

Y, para volver a convertir desde un vector referenciado DQZ al marco de referencia XYZ , la señal del vector de columna debe premultiplicarse por la matriz de transformación de Park inversa:

${\displaystyle u_{XYZ}=K_{P}^{-1}\cdot u_{DQZ}}$.

Las transformadas de Clarke y Park juntas forman la transformada DQZ :

${\displaystyle K_{CP}=K_{P}\cdot K_{C}}$

${\displaystyle \to {\begin{bmatrix}\cos {\left(\theta \right)}&\sin {\left(\theta \right)}&0\\-\sin {\left(\theta \right)}&\cos {\left(\theta \right)}&0\\0&0&1\end{bmatrix}}\cdot {\sqrt {\frac {2}{3}}}{\begin{bmatrix}1&{\frac {-1}{2}}&{\frac {-1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}}$

${\displaystyle \to {\sqrt {\frac {2}{3}}}{\begin{bmatrix}\cos {\left(\theta \right)}&\cos {\left(\theta -{\frac {2\pi }{3}}\right)}&\cos {\left(\theta +{\frac {2\pi }{3}}\right)}\\-\sin {\left(\theta \right)}&-\sin {\left(\theta -{\frac {2\pi }{3}}\right)}&-\sin {\left(\theta +{\frac {2\pi }{3}}\right)}\\{\frac {\sqrt {2}}{2}}&{\frac {\sqrt {2}}{2}}&{\frac {\sqrt {2}}{2}}\end{bmatrix}}}$

La transformada inversa es:

${\displaystyle K_{CP}^{-1}={\sqrt {\frac {2}{3}}}{\begin{bmatrix}\cos {\left(\theta \right)}&-\sin {\left(\theta \right)}&{\frac {\sqrt {2}}{2}}\\\cos {\left(\theta -{\frac {2\pi }{3}}\right)}&-\sin {\left(\theta -{\frac {2\pi }{3}}\right)}&{\frac {\sqrt {2}}{2}}\\\cos {\left(\theta +{\frac {2\pi }{3}}\right)}&-\sin {\left(\theta +{\frac {2\pi }{3}}\right)}&{\frac {\sqrt {2}}{2}}\end{bmatrix}}}$

Para convertir un vector referenciado ABC al marco de referencia DQZ , la señal del vector de columna debe premultiplicarse por la matriz de transformación DQZ:

${\displaystyle u_{DQZ}=K_{CP}\cdot u_{ABC}}$.

Y, para volver a convertir desde un vector referenciado DQZ al marco de referencia ABC , la señal del vector de columna debe premultiplicarse por la matriz de transformación DQZ inversa:

${\displaystyle u_{ABC}=K_{CP}^{-1}\cdot u_{DQZ}}$.

Para comprender mejor esta transformación, se incluye una derivación de la transformación.

Derivación

La derivación de la transformación de Park

La transformada de Park se basa en el concepto de producto escalar y en las proyecciones de vectores sobre otros vectores. En primer lugar, imaginemos dos vectores unitarios, y (los vectores unitarios, o ejes, del nuevo sistema de referencia desde la perspectiva del antiguo sistema de referencia), y un tercer vector arbitrario . Podemos definir los dos vectores unitarios y el vector aleatorio en términos de sus coordenadas cartesianas en el antiguo sistema de referencia: ${\displaystyle {\hat {u}}_{D}}$ ${\displaystyle {\hat {u}}_{Q}}$ ${\displaystyle {\vec {v}}_{XY}}$

${\displaystyle {\hat {u}}_{D}=\cos {\left(\theta \right)}{\hat {u}}_{X}+\sin {\left(\theta \right)}{\hat {u}}_{Y}}$

${\displaystyle {\hat {u}}_{Q}=-\sin {\left(\theta \right)}{\hat {u}}_{X}+\cos {\left(\theta \right)}{\hat {u}}_{Y}}$

${\displaystyle {\vec {v}}_{XY}=v_{X}{\hat {u}}_{X}+v_{Y}{\hat {u}}_{Y}}$,

donde y son los vectores unitarios base del antiguo sistema de coordenadas y es el ángulo entre los vectores unitarios y (es decir, el ángulo entre los dos marcos de referencia). La proyección del vector arbitrario sobre cada uno de los dos nuevos vectores unitarios implica el producto escalar: ${\displaystyle {\hat {u}}_{X}}$ ${\displaystyle {\hat {u}}_{Y}}$ ${\displaystyle \theta }$ ${\displaystyle {\hat {u}}_{X}}$ ${\displaystyle {\hat {u}}_{D}}$

${\displaystyle v_{D}={\hat {u}}_{D}\cdot {\vec {v}}_{XY}}$

${\displaystyle \to \cos {\left(\theta \right)}v_{X}+\sin {\left(\theta \right)}v_{Y}}$

${\displaystyle v_{Q}={\hat {u}}_{Q}\cdot {\vec {v}}_{XY}}$

${\displaystyle \to -\sin {\left(\theta \right)}v_{X}+\cos {\left(\theta \right)}v_{Y}}$.

Por lo tanto, es la proyección de sobre el eje, y es la proyección de sobre el eje. Estos nuevos componentes vectoriales, y , juntos componen el nuevo vector , el vector original en términos del nuevo sistema de referencia DQ . ${\displaystyle v_{D}}$ ${\displaystyle {\vec {v}}_{XY}}$ ${\displaystyle {\hat {u}}_{D}}$ ${\displaystyle v_{Q}}$ ${\displaystyle {\vec {v}}_{XY}}$ ${\displaystyle {\hat {u}}_{Q}}$ ${\displaystyle v_{D}}$ ${\displaystyle v_{Q}}$ ${\displaystyle {\vec {v}}_{DQ}}$ ${\displaystyle {\vec {v}}_{XY}}$

Proyección sobre el marco de referencia DQ . ${\displaystyle {\vec {v}}_{XY}}$

Observe que el ángulo positivo anterior provocó que el vector arbitrario rotara hacia atrás cuando se lo trasladó al nuevo sistema de referencia DQ . En otras palabras, su ángulo con respecto al nuevo sistema de referencia es menor que su ángulo con respecto al sistema de referencia anterior. Esto se debe a que el sistema de referencia, no el vector, se rotó hacia adelante. En realidad, una rotación hacia adelante del sistema de referencia es idéntica a una rotación negativa del vector. Si el sistema de referencia anterior estuviera rotando hacia adelante, como en los sistemas eléctricos trifásicos, entonces el vector DQ resultante permanece estacionario. ${\displaystyle \theta }$

Una sola ecuación matricial puede resumir la operación anterior:

${\displaystyle {\vec {v}}_{DQ}={\begin{bmatrix}\cos {\left(\theta \right)}&\sin {\left(\theta \right)}\\-\sin {\left(\theta \right)}&\cos {\left(\theta \right)}\end{bmatrix}}\cdot {\vec {v}}_{XY}}$.

Este tensor se puede ampliar a problemas tridimensionales, en los que el eje sobre el que se produce la rotación no se ve afectado. En el siguiente ejemplo, la rotación se produce sobre el eje Z , pero se podría haber elegido cualquier eje:

${\displaystyle K_{P}={\begin{bmatrix}\cos {\left(\theta \right)}&\sin {\left(\theta \right)}&0\\-\sin {\left(\theta \right)}&\cos {\left(\theta \right)}&0\\0&0&1\end{bmatrix}}}$.

Desde una perspectiva de álgebra lineal, esto es simplemente una rotación en el sentido de las agujas del reloj alrededor del eje z y es matemáticamente equivalente a las fórmulas de diferencia de ángulos trigonométricos .

La derivación de la transformada de Clarke

Vectores de base unitaria ABC

Consideremos un espacio tridimensional con vectores de base unitarios A , B y C. La esfera en la figura siguiente se utiliza para mostrar la escala del marco de referencia para el contexto y la caja se utiliza para proporcionar un contexto rotacional.

Vectores base unitarios ABC .

Por lo general, en ingeniería eléctrica (o en cualquier otro contexto que utilice sistemas trifásicos), los componentes trifásicos se muestran en una perspectiva bidimensional. Sin embargo, dado que las tres fases pueden cambiar de forma independiente, por definición son ortogonales entre sí. Esto implica una perspectiva tridimensional, como se muestra en la figura anterior. Por lo tanto, la perspectiva bidimensional muestra en realidad la proyección de la realidad tridimensional sobre un plano.

Perspectiva bidimensional de una realidad tridimensional.

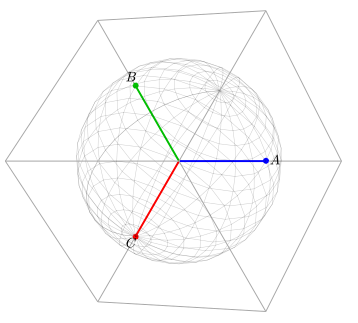
Los problemas trifásicos se describen típicamente como si operaran dentro de este plano. En realidad, es probable que el problema sea un problema de fase equilibrada (es decir, v _A + v _B + v _C = 0) y el vector neto

${\displaystyle {\vec {v}}=v_{A}{\hat {u}}_{A}+v_{B}{\hat {u}}_{B}+v_{C}{\hat {u}}_{C}}$

Siempre está en este plano.

Vectores de base unitaria del AYC

Para construir la transformada de Clarke, en realidad utilizamos la transformada de Park en dos pasos. Nuestro objetivo es rotar el eje C hacia la esquina de la caja. De esta manera, el eje C rotado será ortogonal al plano de la perspectiva bidimensional mencionada anteriormente. El primer paso para construir la transformada de Clarke requiere rotar el sistema de referencia ABC sobre el eje A. Por lo tanto, esta vez, el 1 estará en el primer elemento de la transformada de Park:

${\displaystyle K_{1}={\begin{bmatrix}1&0&0\\0&\cos {\left(-{\frac {\pi }{4}}\right)}&\sin {\left(-{\frac {\pi }{4}}\right)}\\0&-\sin {\left(-{\frac {\pi }{4}}\right)}&\cos {\left(-{\frac {\pi }{4}}\right)}\end{bmatrix}}}$

${\displaystyle \to {\begin{bmatrix}1&0&0\\0&{\frac {1}{\sqrt {2}}}&-{\frac {1}{\sqrt {2}}}\\0&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}}$

La siguiente figura muestra cómo se rota el sistema de referencia ABC al sistema de referencia AYC' cuando cualquier vector se premultiplica por la matriz K _1. Los ejes C' e Y ahora apuntan a los puntos medios de los bordes de la caja, pero la magnitud del sistema de referencia no ha cambiado (es decir, la esfera no creció ni se encogió). Esto se debe al hecho de que la norma del tensor K ₁ es 1: || K ₁ || = 1. Esto significa que cualquier vector en el sistema de referencia ABC continuará teniendo la misma magnitud cuando se rota al sistema de referencia AYC' .

Vectores de base unitaria de AYC . Los ejes C' e Y ahora apuntan a los bordes de la caja, pero la magnitud no ha cambiado.

Los vectores de base unitaria XYZ

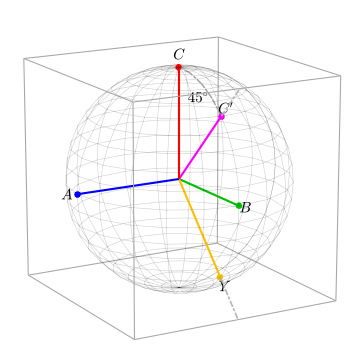
A continuación, el siguiente tensor gira el vector sobre el nuevo eje Y en sentido antihorario con respecto al eje Y (el ángulo se eligió de modo que el eje C' apuntara hacia la esquina de la caja):

${\displaystyle K_{2}={\begin{bmatrix}\cos {\left(\theta \right)}&0&-\sin {\left(\theta \right)}\\0&1&0\\\sin {\left(\theta \right)}&0&\cos {\left(\theta \right)}\end{bmatrix}}}$

${\displaystyle \theta =\cos ^{-1}\left({\sqrt {\frac {2}{3}}}\right)\to 35.26^{\circ }}$,

o

${\displaystyle K_{2}={\begin{bmatrix}{\sqrt {\frac {2}{3}}}&0&-{\frac {1}{\sqrt {3}}}\\0&1&0\\{\frac {1}{\sqrt {3}}}&0&{\sqrt {\frac {2}{3}}}\end{bmatrix}}}$.

Observe que la distancia desde el centro de la esfera hasta el punto medio del borde de la caja es √ 2, pero desde el centro de la esfera hasta la esquina de la caja es √ 3. De ahí proviene el ángulo de 35,26°. El ángulo se puede calcular utilizando el producto escalar. Sea el vector unitario en la dirección de C' y sea un vector unitario en la dirección de la esquina de la caja en . Porque donde es el ángulo entre y tenemos ${\displaystyle {\vec {m}}=\left(0,{\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}\right)}$ ${\displaystyle {\vec {n}}=\left({\frac {1}{\sqrt {3}}},{\frac {1}{\sqrt {3}}},{\frac {1}{\sqrt {3}}}\right)}$ ${\displaystyle {\vec {n}}=\left(1,1,1\right)}$ ${\displaystyle {\vec {m}}\cdot {\vec {n}}=|{\vec {m}}||{\vec {n}}|\cos \theta ,}$ ${\displaystyle \theta }$ ${\displaystyle {\vec {m}}}$ ${\displaystyle {\vec {n}},}$

${\displaystyle \left(0,{\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}\right)\cdot \left({\frac {1}{\sqrt {3}}},{\frac {1}{\sqrt {3}}},{\frac {1}{\sqrt {3}}}\right)=\cos \theta }$

${\displaystyle \cos \theta =0+{\frac {\sqrt {2}}{2{\sqrt {3}}}}+{\frac {\sqrt {2}}{2{\sqrt {3}}}}={\sqrt {\frac {2}{3}}}}$

${\displaystyle \theta =\cos ^{-1}\left({\sqrt {\frac {2}{3}}}\right)}$

${\displaystyle \theta =35.26^{\circ }.}$

La norma de la matriz K ₂ también es 1, por lo que tampoco cambia la magnitud de ningún vector premultiplicado por la matriz K ₂ .

Vectores de base unitaria XYZ . El eje Z (eje C' rotado ) ahora apunta hacia la esquina del cuadro.

El plano cero

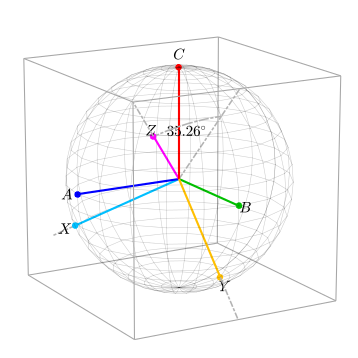
En este punto, el eje Z es ahora ortogonal al plano en el que se puede encontrar cualquier vector ABC sin un componente de modo común. Cualquier forma de onda de vector ABC balanceada (un vector sin un modo común) se desplazará por este plano. Este plano se denominará plano cero y se muestra a continuación con el contorno hexagonal.

Plano de los vectores sin modo común indicado por el contorno hexagonal. El eje Z es ortogonal a este plano y el eje X es paralelo a la proyección del eje A sobre el plano cero.

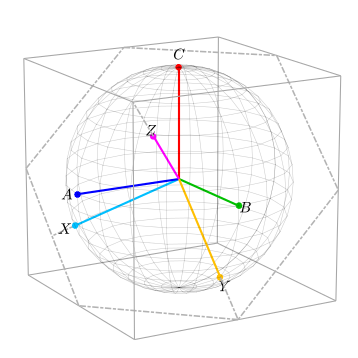
Los vectores base X e Y están en el plano cero. Observe que el eje X es paralelo a la proyección del eje A sobre el plano cero. El eje X es ligeramente más grande que la proyección del eje A sobre el plano cero. Es más grande por un factor de √ 3/2 . El vector arbitrario no cambió de magnitud a través de esta conversión del marco de referencia ABC al marco de referencia XYZ (es decir, la esfera no cambió de tamaño). Esto es cierto para la forma invariante de potencia de la transformada de Clarke. La siguiente figura muestra la perspectiva bidimensional común de los marcos de referencia ABC y XYZ .

Perspectiva bidimensional de los marcos de referencia ABC y XYZ .

Puede parecer extraño que, aunque la magnitud del vector no haya cambiado, la magnitud de sus componentes sí lo haya hecho (es decir, los componentes X e Y son más largos que los componentes A , B y C ). Tal vez esto se pueda entender intuitivamente considerando que para un vector sin modo común, lo que tomó tres valores ( componentes A , B y C ) para expresarse, ahora solo toma 2 ( componentes X e Y ) ya que el componente Z es cero. Por lo tanto, los valores de los componentes X e Y deben ser mayores para compensar.

Combinación de tensores

La matriz de transformación de Clarke invariante de potencia es una combinación de los tensores K ₁ y K _{2 :}

${\displaystyle K_{C}=\underbrace {\begin{bmatrix}{\sqrt {\frac {2}{3}}}&0&-{\frac {1}{\sqrt {3}}}\\0&1&0\\{\frac {1}{\sqrt {3}}}&0&{\sqrt {\frac {2}{3}}}\end{bmatrix}} _{K_{2}}\cdot \underbrace {\begin{bmatrix}1&0&0\\0&{\frac {1}{\sqrt {2}}}&-{\frac {1}{\sqrt {2}}}\\0&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}} _{K_{1}}}$,

o

${\displaystyle K_{C}={\sqrt {\frac {2}{3}}}\cdot {\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}}$

${\displaystyle \to {\begin{bmatrix}{\frac {2}{\sqrt {6}}}&-{\frac {1}{\sqrt {6}}}&-{\frac {1}{\sqrt {6}}}\\0&{\frac {1}{\sqrt {2}}}&-{\frac {1}{\sqrt {2}}}\\{\frac {1}{\sqrt {3}}}&{\frac {1}{\sqrt {3}}}&{\frac {1}{\sqrt {3}}}\end{bmatrix}}}$.

Tenga en cuenta que cuando se multiplica, la fila inferior de la matriz K _{C es 1/} √ 3 , no 1/3. (Edith Clarke utilizó 1/3 para el caso de variante de potencia). El componente Z no es exactamente el promedio de los componentes A , B y C . Si solo se cambiaran los elementos de la fila inferior para que fueran 1/3, entonces la esfera se aplastaría a lo largo del eje Z. Esto significa que el componente Z no tendría la misma escala que los componentes X e Y.

Marco K _C (azul) y matriz original de Edith (verde).

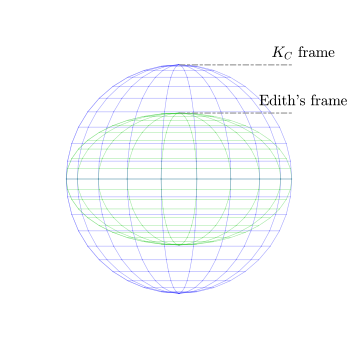
Como se ha escrito anteriormente, la norma de la matriz de transformación de Clarke sigue siendo 1, lo que significa que solo rota un vector ABC pero no lo escala. No se puede decir lo mismo de la transformación original de Clarke.

Es fácil verificar (por multiplicación de matrices) que la inversa de K _C es

${\displaystyle K_{C}^{-1}={\begin{bmatrix}{\frac {2}{\sqrt {6}}}&0&{\frac {1}{\sqrt {3}}}\\-{\frac {1}{\sqrt {6}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {3}}}\\-{\frac {1}{\sqrt {6}}}&-{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {3}}}\end{bmatrix}}}$

Forma variante de potencia

A veces es conveniente escalar la matriz de transformación de Clarke de modo que el eje X sea la proyección del eje A sobre el plano cero. Para ello, aplicamos uniformemente un factor de escala de √ 2/3 y un radical ² √ ^{1/ [ ¿por qué? ]} al componente cero para obtener la matriz de transformación de Clarke variante de potencia:

${\displaystyle K_{\hat {C}}={\sqrt {\frac {2}{3}}}\cdot \underbrace {{\sqrt {\frac {2}{3}}}\cdot {\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{2}}&{\frac {1}{2}}&{\frac {1}{2}}\end{bmatrix}}} _{K_{C}}}$

${\displaystyle \to {\frac {2}{3}}{\begin{bmatrix}1&-{\frac {1}{2}}&-{\frac {1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{2}}&{\frac {1}{2}}&{\frac {1}{2}}\end{bmatrix}}}$

o

${\displaystyle K_{\hat {C}}={\begin{bmatrix}{\frac {2}{3}}&-{\frac {1}{3}}&-{\frac {1}{3}}\\0&{\frac {1}{\sqrt {3}}}&-{\frac {1}{\sqrt {3}}}\\{\frac {1}{3}}&{\frac {1}{3}}&{\frac {1}{3}}\end{bmatrix}}}$.

Esto necesariamente reducirá la esfera por un factor de √ 2/3 como se muestra a continuación. Observe que este nuevo eje X es exactamente la proyección del eje A sobre el plano cero.

El marco de referencia XYZ escalado de la transformada de Clarke variante de potencia.

Con la transformada de Clarke variante de potencia, la magnitud del vector arbitrario es menor en el marco de referencia XYZ que en el marco de referencia ABC (la norma de la transformada es √ 2/3 ), pero las magnitudes de los componentes individuales del vector son las mismas (cuando no hay un modo común). Por lo tanto, como ejemplo, una señal definida por

${\displaystyle {\begin{bmatrix}A\\B\\C\end{bmatrix}}={\begin{bmatrix}\cos {\left(\omega t\right)}\\\cos {\left(\omega t-{\frac {2\pi }{3}}\right)}\\\cos {\left(\omega t+{\frac {2\pi }{3}}\right)}\end{bmatrix}}}$

se convierte, en el marco de referencia XYZ ,

${\displaystyle {\begin{bmatrix}X\\Y\\Z\end{bmatrix}}={\begin{bmatrix}\cos {\left(\omega t\right)}\\\cos {\left(\omega t-{\frac {\pi }{2}}\right)}\\0\end{bmatrix}}}$,

un nuevo vector cuyos componentes son de la misma magnitud que los componentes originales: 1. En muchos casos, esta es una cualidad ventajosa de la transformada de Clarke variante de potencia.

La transformación DQZ

La transformación DQZ utiliza la transformada de Clarke para convertir los vectores referenciados por ABC en dos componentes de modo diferencial (es decir, X e Y ) y un componente de modo común (es decir, Z ) y luego aplica la transformada de Park para rotar el marco de referencia sobre el eje Z en un ángulo determinado. El componente X se convierte en el componente D , que está en alineación directa con el vector de rotación, y el componente Y se convierte en el componente Q , que está en un ángulo de cuadratura con el componente directo. La transformada DQZ es

${\displaystyle K_{CP}=K_{P}\cdot K_{C}}$

${\displaystyle \to {\begin{bmatrix}\cos {\left(\theta \right)}&\sin {\left(\theta \right)}&0\\-\sin {\left(\theta \right)}&\cos {\left(\theta \right)}&0\\0&0&1\end{bmatrix}}\cdot {\sqrt {\frac {2}{3}}}{\begin{bmatrix}1&{\frac {-1}{2}}&{\frac {-1}{2}}\\0&{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {3}}{2}}\\{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}&{\frac {1}{\sqrt {2}}}\end{bmatrix}}}$.

Ejemplo

En los sistemas eléctricos, muy a menudo los valores A , B y C oscilan de tal manera que el vector neto gira. En un sistema equilibrado, el vector gira alrededor del eje Z. Muy a menudo, resulta útil rotar el marco de referencia de modo que la mayoría de los cambios en los valores abc, debido a este giro, se cancelen y cualquier variación más fina se vuelva más obvia. Esto es increíblemente útil ya que ahora transforma el sistema en un sistema lineal invariante en el tiempo.

La transformación DQZ puede considerarse en términos geométricos como la proyección de las tres cantidades de fase sinusoidal separadas sobre dos ejes que giran con la misma velocidad angular que las cantidades de fase sinusoidal.

Ejemplo DQZ.

Arriba se muestra la transformada DQZ aplicada al estator de una máquina sincrónica. Hay tres devanados separados por 120 grados físicos. Las tres corrientes de fase son iguales en magnitud y están separadas entre sí por 120 grados eléctricos. Las tres corrientes de fase están retrasadas respecto de sus voltajes de fase correspondientes en . Los ejes DQ se muestran girando con una velocidad angular igual a , la misma velocidad angular que los voltajes y corrientes de fase. El eje D forma un ángulo con el devanado de fase A que se ha elegido como referencia. Las corrientes y son cantidades de corriente continua constantes. ${\displaystyle \delta }$ ${\displaystyle \omega }$ ${\displaystyle \theta =\omega t}$ ${\displaystyle I_{D}}$ ${\displaystyle I_{Q}}$

Comparación con otras transformaciones

La transformación del parque

La transformación propuesta originalmente por Park en ^[5] difiere ligeramente de la que se presentó anteriormente. En la transformación de Park, el eje q está por delante del eje d, qd0, y el ángulo es el ángulo entre la fase a y el eje d, como se muestra a continuación: ${\displaystyle \theta }$

${\displaystyle P={\frac {2}{3}}{\begin{bmatrix}\cos(\theta )&\cos(\theta -{\frac {2\pi }{3}})&\cos(\theta +{\frac {2\pi }{3}})\\-\sin(\theta )&-\sin(\theta -{\frac {2\pi }{3}})&-\sin(\theta +{\frac {2\pi }{3}})\\{\frac {1}{2}}&{\frac {1}{2}}&{\frac {1}{2}}\end{bmatrix}}}$

y

${\displaystyle P^{-1}={\begin{bmatrix}\cos(\theta )&-\sin(\theta )&1\\\cos(\theta -{\frac {2\pi }{3}})&-\sin(\theta -{\frac {2\pi }{3}})&1\\\cos(\theta +{\frac {2\pi }{3}})&-\sin(\theta +{\frac {2\pi }{3}})&1\end{bmatrix}}}$

D. Holmes y T. Lipo, Modulación de ancho de pulso para convertidores de potencia: principios y práctica, Wiley-IEEE Press, 2003, y

P. Krause, O. Wasynczuk y S. Sudhoff, Análisis de maquinaria eléctrica y sistemas de accionamiento, 2.ª ed., Piscataway, Nueva Jersey: IEEE Press, 2002.

Transformación αβγ

La transformada dqo es conceptualmente similar a la transformada αβγ . Mientras que la transformada dqo es la proyección de las magnitudes de fase sobre un marco de referencia de dos ejes giratorio, la transformada αβγ puede considerarse como la proyección de las magnitudes de fase sobre un marco de referencia de dos ejes estacionario.

Referencias

Referencias en línea

1. "Realizar la transformación de una señal trifásica (abc) a un marco de referencia rotatorio dq0 o la inversa". Simulink . 2018-09-27 . Consultado el 2019-01-11 .
2. Mihailovic, Zoran (26 de junio de 1998). "Modelado y diseño de control de sistemas de accionamiento PMSM con alimentación por VSI y carga activa" (PDF) . ETD . Consultado el 11 de enero de 2019 .
3. Kamalakannan, C.; Suresh, LP; Dash, SS; Panigrahi, BK (2014). Electrónica de potencia y sistemas de energía renovable: actas de ICPERES 2014. Apuntes de clases de ingeniería eléctrica. Springer India. pág. 1029. ISBN 978-81-322-2119-7. Recuperado el 11 de enero de 2019 .
4. RH Park Teoría de dos reacciones de máquinas síncronas AIEE Transactions 48:716–730 (1929).
5. RH Park, "Teoría de dos reacciones de las máquinas sincrónicas: método generalizado de análisis, parte I", en Transactions of the American Institute of Electrical Engineers, vol. 48, núm. 3, págs. 716-727, julio de 1929, doi: 10.1109/T-AIEE.1929.5055275

Referencias generales

• CJ O'Rourke et al. "Una interpretación geométrica de los marcos de referencia y las transformaciones: dq0, Clarke y Park", en IEEE Transactions on Energy Conversion, vol. 34, n.º 4, págs. 2070-2083, diciembre de 2019.
• Componentes simétricos para la ingeniería de sistemas de potencia , J. Lewis Blackburn , Marcel Dekker, Nueva York (1993). ISBN 0-8247-8767-6 
• Zhang et al. Un inversor trifásico con una pata neutra con modulación vectorial espacial. Actas de la conferencia IEEE APEC '97 (1997).
• TALipo, “Un enfoque vectorial cartesiano para la teoría de referencia de máquinas de CA”, Conferencia internacional sobre máquinas eléctricas, Lausana, 18-24 de septiembre de 1984.

Véase también

• Componentes simétricos
• ${\displaystyle \alpha \beta \gamma }$transformar
• Control vectorial (motor)