Lema de cobertura de Vitali

Resultado combinatorio y geométrico utilizado en la teoría de la medida de los espacios euclidianos

En matemáticas , el lema de recubrimiento de Vitali es un resultado combinatorio y geométrico comúnmente utilizado en la teoría de la medida de los espacios euclidianos . Este lema es un paso intermedio, de interés independiente, en la demostración del teorema de recubrimiento de Vitali . El teorema de recubrimiento se atribuye al matemático italiano Giuseppe Vitali . ^[1] El teorema establece que es posible cubrir, hasta un conjunto despreciable en el sentido de Lebesgue , un subconjunto dado E de R ^d mediante una familia disjunta extraída de un recubrimiento de Vitali de E .

Lema de cobertura de Vitali

Visualización del lema en . ${\displaystyle \mathbb {R} ^{1}}$

Arriba: una colección de bolas; las bolas verdes son la subcolección disjunta. Abajo: la subcolección con tres veces el radio cubre todas las bolas.

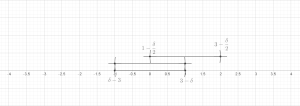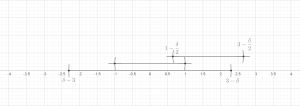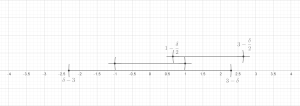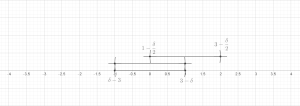
Existen dos versiones básicas del lema, una versión finita y una versión infinita. Ambos lemas se pueden demostrar en el contexto general de un espacio métrico ; por lo general, estos resultados se aplican al caso especial del espacio euclidiano . En ambos teoremas utilizaremos la siguiente notación: si es una pelota y , escribiremos para la pelota . ${\displaystyle \mathbb {R} ^{d}}$ ${\textstyle B=B(x,r)}$ ${\displaystyle c\geq 0}$ ${\displaystyle cB}$ ${\textstyle B(x,cr)}$

Versión finita

Teorema (Lema de Recubrimiento Finito). Sea cualquier colección finita de bolas contenidas en un espacio métrico arbitrario. Entonces existe una subcolección de estas bolas que son disjuntas y satisfacen Demostración: Sin pérdida de generalidad, suponemos que la colección de bolas no está vacía; es decir, n  > 0. Sea la bola de radio más grande. Inductivamente, supongamos que se han elegido. Si hay alguna bola en que es disjunta de , sea dicha bola con radio máximo (deshaciendo los empates arbitrariamente), de lo contrario, establecemos m  := k y terminamos la definición inductiva. ${\displaystyle B_{1},\dots ,B_{n}}$ ${\displaystyle B_{j_{1}},B_{j_{2}},\dots ,B_{j_{m}}}$ $${\displaystyle B_{1}\cup B_{2}\cup \dots \cup B_{n}\subseteq 3B_{j_{1}}\cup 3B_{j_{2}}\cup \dots \cup 3B_{j_{m}}.}$$ ${\displaystyle B_{j_{1}}}$ ${\displaystyle B_{j_{1}},\dots ,B_{j_{k}}}$ ${\displaystyle B_{1},\dots ,B_{n}}$ ${\displaystyle B_{j_{1}}\cup B_{j_{2}}\cup \dots \cup B_{j_{k}}}$ ${\displaystyle B_{j_{k+1}}}$

Ahora establecemos . Queda por demostrar que para cada . Esto es claro si . De lo contrario, necesariamente existe algún tal que interseca a . Elegimos el mínimo posible y notamos que el radio de es al menos tan grande como el de . La desigualdad triangular entonces implica que , como se necesita. Esto completa la prueba de la versión finita. ${\textstyle X:=\bigcup _{k=1}^{m}3\,B_{j_{k}}}$ ${\displaystyle B_{i}\subset X}$ ${\displaystyle i=1,2,\dots ,n}$ ${\displaystyle i\in \{j_{1},\dots ,j_{m}\}}$ ${\displaystyle k\in \{1,\dots ,m\}}$ ${\displaystyle B_{i}}$ ${\displaystyle B_{j_{k}}}$ ${\displaystyle k}$ ${\displaystyle B_{j_{k}}}$ ${\displaystyle B_{i}}$ ${\displaystyle B_{i}\subset 3\,B_{j_{k}}\subset X}$

Versión infinita

Teorema (Lema de recubrimiento infinito). Sea una colección arbitraria de bolas en un espacio métrico separable tal que donde denota el radio de la bola B . Entonces existe una subcolección numerable tal que las bolas de son disjuntas por pares y satisfacen Y además, cada una interseca alguna con . ${\displaystyle \mathbf {F} }$ $${\displaystyle R:=\sup \,\{\mathrm {rad} (B):B\in \mathbf {F} \}<\infty }$$ ${\displaystyle \mathrm {rad} (B)}$ ${\displaystyle \mathbf {G} \subset \mathbf {F} }$ ${\displaystyle \mathbf {G} }$ $${\displaystyle \bigcup _{B\in \mathbf {F} }B\subseteq \bigcup _{C\in \mathbf {G} }5\,C.}$$ ${\displaystyle B\in \mathbf {F} }$ ${\displaystyle C\in \mathbf {G} }$ ${\displaystyle B\subset 5C}$

Demostración: Considérese la partición de F en subcolecciones F _n , n  ≥ 0, definidas por

${\displaystyle \mathbf {F} _{n}=\{B\in \mathbf {F} :2^{-n-1}R<{\text{rad}}(B)\leq 2^{-n}R\}.}$

Es decir, consta de las bolas B cuyo radio está en (2 ^{− n −1} R , 2 ^{− n} R ]. Una secuencia G _n , con G _n  ⊂ F _n , se define inductivamente de la siguiente manera. Primero, hagamos H ₀  = F ₀ y sea G ₀ una subcolección disjunta máxima de H ₀ (tal subcolección existe por el lema de Zorn ). Suponiendo que se han seleccionado G ₀ ,..., G _{n , sea} ${\textstyle \mathbf {F} _{n}}$

${\displaystyle \mathbf {H} _{n+1}=\{B\in \mathbf {F} _{n+1}:\ B\cap C=\emptyset ,\ \ \forall C\in \mathbf {G} _{0}\cup \mathbf {G} _{1}\cup \dots \cup \mathbf {G} _{n}\},}$

y sea G _{n +1} una subcolección disjunta máxima de H _{n +1} . La subcolección

${\displaystyle \mathbf {G} :=\bigcup _{n=0}^{\infty }\mathbf {G} _{n}}$

de F satisface los requisitos del teorema: G es una colección disjunta, y por lo tanto es contable ya que el espacio métrico dado es separable. Además, cada bola B  ∈ F interseca una bola C  ∈ G tal que B  ⊂ 5  C .
De hecho, si se nos da algún , debe haber algún n tal que B pertenezca a F _n . O bien B no pertenece a H _n , lo que implica n  > 0 y significa que B interseca una bola de la unión de G ₀ , ..., G _{n −1} , o B  ∈ H _n y por maximalidad de G _n , B interseca una bola en G _n . En cualquier caso, B interseca una bola C que pertenece a la unión de G ₀ , ..., G _n . Una bola C de este tipo debe tener un radio mayor que 2 ^{− n −1} R . Como el radio de B es menor o igual a 2 ^{− n} R, podemos concluir por la desigualdad triangular que B  ⊂ 5  C, como se afirma. De esto se sigue inmediatamente, completando la demostración. ^[2] ${\displaystyle B\in \mathbf {F} }$ ${\displaystyle \bigcup _{B\in \mathbf {F} }B\subseteq \bigcup _{C\in \mathbf {G} }5\,C}$

Observaciones

• En la versión infinita , la colección inicial de bolas puede ser contable o incontable . En un espacio métrico separable, cualquier colección de bolas disjunta por pares debe ser contable. En un espacio no separable, el mismo argumento muestra que existe una subfamilia disjunta por pares, pero esa familia no necesita ser contable.
• El resultado puede fallar si los radios no están acotados: considere la familia de todas las bolas centradas en 0 en R ^d ; cualquier subfamilia disjunta consiste en solo una bola B , y 5  B no contiene todas las bolas de esta familia.
• La constante 5 no es óptima. Si se utiliza la escala c ^{− n} , c  > 1, en lugar de 2 ^{− n} para definir F _n , el valor final es 1 + 2 c en lugar de 5. Cualquier constante mayor que 3 da un enunciado correcto del lema, pero no 3.
• Utilizando un análisis más fino, cuando la colección original F es una cobertura de Vitali de un subconjunto E de R ^d , se demuestra que la subcolección G , definida en la prueba anterior, cubre E hasta un conjunto despreciable en términos de Lebesgue. ^[3]

Aplicaciones y modo de uso

Una aplicación del lema de Vitali es la demostración de la desigualdad máxima de Hardy-Littlewood . Como en esta demostración, el lema de Vitali se utiliza con frecuencia cuando, por ejemplo, consideramos la medida de Lebesgue de dimensión d , , de un conjunto E  ⊂ R ^d , que sabemos que está contenido en la unión de una cierta colección de bolas , cada una de las cuales tiene una medida que podemos calcular más fácilmente, o tiene una propiedad especial que nos gustaría explotar. Por lo tanto, si calculamos la medida de esta unión, tendremos un límite superior en la medida de E . Sin embargo, es difícil calcular la medida de la unión de todas estas bolas si se superponen. Por el lema de Vitali, podemos elegir una subcolección que sea disjunta y tal que . Por lo tanto, ${\displaystyle \lambda _{d}}$ ${\displaystyle \{B_{j}:j\in J\}}$ ${\displaystyle \left\{B_{j}:j\in J'\right\}}$ ${\textstyle \bigcup _{j\in J'}5B_{j}\supset \bigcup _{j\in J}B_{j}\supset E}$

${\displaystyle \lambda _{d}(E)\leq \lambda _{d}{\biggl (}\bigcup _{j\in J}B_{j}{\biggr )}\leq \lambda _{d}{\biggl (}\bigcup _{j\in J'}5B_{j}{\biggr )}\leq \sum _{j\in J'}\lambda _{d}(5B_{j}).}$

Ahora bien, dado que aumentar el radio de una bola de dimensión d por un factor de cinco aumenta su volumen por un factor de 5 ^d , sabemos que

${\displaystyle \sum _{j\in J'}\lambda _{d}(5B_{j})=5^{d}\sum _{j\in J'}\lambda _{d}(B_{j})}$

y por lo tanto

${\displaystyle \lambda _{d}(E)\leq 5^{d}\sum _{j\in J'}\lambda _{d}(B_{j}).}$

Teorema de cobertura de Vitali

En el teorema de cubrimiento, el objetivo es cubrir, hasta un "conjunto despreciable", un conjunto dado E  ⊆  R ^d por una subcolección disjunta extraída de un cubrimiento de Vitali para  E  : una clase de Vitali o cubrimiento de Vitali para E es una colección de conjuntos tales que, para cada x  ∈  E y δ  > 0, hay un conjunto U en la colección tal que x  ∈  U y el diámetro de U es distinto de cero y menor que  δ . ${\displaystyle {\mathcal {V}}}$ ${\displaystyle {\mathcal {V}}}$

En el contexto clásico de Vitali, ^[1] el conjunto despreciable es un conjunto despreciable de Lebesgue , pero también se han considerado medidas distintas de la medida de Lebesgue y espacios distintos de R ^{d , como se muestra en la sección correspondiente a continuación.}

La siguiente observación es útil: si es una cobertura de Vitali para E y si E está contenido en un conjunto abierto Ω ⊆  R ^d , entonces la subcolección de conjuntos U en que están contenidos en Ω también es una cobertura de Vitali para E . ${\displaystyle {\mathcal {V}}}$ ${\displaystyle {\mathcal {V}}}$

Teorema de cobertura de Vitali para la medida de Lebesgue

El siguiente teorema de cobertura para la medida de Lebesgue λ _d se debe a Lebesgue (1910). Una colección de subconjuntos medibles de R ^d es una familia regular (en el sentido de Lebesgue ) si existe una constante C tal que ${\displaystyle {\mathcal {V}}}$

${\displaystyle \operatorname {diam} (V)^{d}\leq C\,\lambda _{d}(V)}$

para cada conjunto V en la colección . La familia de cubos es un ejemplo de familia regular , como lo es la familia de rectángulos en R ² tales que la razón de los lados se mantiene entre m ⁻¹ y m , para algún m  ≥ 1 fijo. Si se da una norma arbitraria en R ^d , la familia de bolas para la métrica asociada a la norma es otro ejemplo. Por el contrario, la familia de todos los rectángulos en R ² no es regular. ${\displaystyle {\mathcal {V}}}$
${\displaystyle {\mathcal {V}}}$ ${\displaystyle {\mathcal {V}}(m)}$

Teorema  —  Sea E  ⊆  R ^d un conjunto medible con medida de Lebesgue finita, y sea una familia regular de subconjuntos cerrados de R ^d que es un recubrimiento de Vitali para E . Entonces existe una subcolección disjunta finita o infinitamente numerable tal que ${\displaystyle {\mathcal {V}}}$ ${\displaystyle \{U_{j}\}\subseteq {\mathcal {V}}}$ $${\displaystyle \lambda _{d}{\biggl (}E\setminus \bigcup _{j}U_{j}{\biggr )}=0.}$$

El resultado original de Vitali (1908) es un caso especial de este teorema, en el que d  = 1 y es una colección de intervalos que constituye una cobertura de Vitali para un subconjunto medible E de la recta real que tiene medida finita. El teorema anterior sigue siendo válido sin suponer que E tiene medida finita. Esto se obtiene aplicando el resultado de la cobertura en el caso de medida finita, para cada entero n  ≥ 0, a la porción de E contenida en el anillo abierto Ω _n de puntos x tal que n  < | x | < n +1. ^[4] ${\displaystyle {\mathcal {V}}}$

Un teorema de recubrimiento algo relacionado es el teorema de recubrimiento de Besicovitch . A cada punto a de un subconjunto A  ⊆  R ^d , se le asigna una bola euclidiana B ( a ,  r _a ) con centro a y radio positivo r _a . Luego, como en el lema de recubrimiento de Vitali, se selecciona una subcolección de estas bolas para cubrir A de una manera específica. Las principales diferencias entre el teorema de recubrimiento de Besicovitch y el lema de recubrimiento de Vitali son que, por un lado, el requisito de disyunción de Vitali se relaja al hecho de que el número N _x de las bolas seleccionadas que contienen un punto arbitrario x  ∈  R ^d está acotado por una constante B _d que depende solo de la dimensión d ; por otro lado, las bolas seleccionadas cubren el conjunto A de todos los centros dados. ^[5]

Teorema de recubrimiento de Vitali para la medida de Hausdorff

Se puede tener un objetivo similar al considerar la medida de Hausdorff en lugar de la medida de Lebesgue. En ese caso se aplica el siguiente teorema: ^[6]

Teorema  —  Sea H ^s una medida de Hausdorff s -dimensional, sea E  ⊆  R ^d un conjunto H ^s - medible y una clase Vitali de conjuntos cerrados para E . Entonces existe una subcolección disjunta (finita o infinitamente numerable) tal que o ${\displaystyle {\mathcal {V}}}$ ${\displaystyle \{U_{j}\}\subseteq {\mathcal {V}}}$ $${\displaystyle H^{s}\left(E\setminus \bigcup _{j}U_{j}\right)=0}$$ $${\displaystyle \sum _{j}\operatorname {diam} (U_{j})^{s}=\infty .}$$

Además, si E tiene una medida de Hausdorff finita de dimensión s , entonces para cualquier ε  > 0, podemos elegir esta subcolección { U _j } tal que

${\displaystyle H^{s}(E)\leq \sum _{j}\mathrm {diam} (U_{j})^{s}+\varepsilon .}$

Este teorema implica el resultado de Lebesgue dado anteriormente. De hecho, cuando s  = d , la medida de Hausdorff H ^s en R ^d coincide con un múltiplo de la medida de Lebesgue de dimensión d . Si una colección disjunta es regular y está contenida en una región medible B con medida de Lebesgue finita, entonces ${\displaystyle \{U_{j}\}}$

${\displaystyle \sum _{j}\operatorname {diam} (U_{j})^{d}\leq C\sum _{j}\lambda _{d}(U_{j})\leq C\,\lambda _{d}(B)<+\infty }$

lo que excluye la segunda posibilidad de la primera afirmación del teorema anterior. De ello se deduce que E está cubierto, hasta un conjunto despreciable desde el punto de vista de Lebesgue, por la subcolección disjunta seleccionada.

Del lema de recubrimiento al teorema de recubrimiento

El lema de recubrimiento se puede utilizar como paso intermedio en la prueba de la siguiente forma básica del teorema de recubrimiento de Vitali.

Teorema  —  Para cada subconjunto E de R ^d y cada cubierta de Vitali de E por una colección F de bolas cerradas, existe una subcolección disjunta G que cubre E hasta un conjunto despreciable en el sentido de Lebesgue.

Demostración: Sin pérdida de generalidad, se puede suponer que todas las bolas en F son no degeneradas y tienen un radio menor o igual a 1. Por la forma infinita del lema de recubrimiento, existe una subcolección disjunta contable de F tal que cada bola B  ∈ F interseca una bola C  ∈ G para la cual B  ⊂ 5  C . Sea r  > 0, y sea Z el conjunto de puntos z  ∈ E que no están contenidos en ninguna bola de G y pertenecen a la bola abierta B ( r ) de radio r , centrada en 0. Es suficiente mostrar que Z es Lebesgue-despreciable, para cada r dado . ${\displaystyle \mathbf {G} }$

Sea la subcolección de aquellas bolas en G que se encuentran con B ( r ). Nótese que puede ser finito o numerablemente infinito. Sea z  ∈ Z fijo. Para cada N, z no pertenece al conjunto cerrado por la definición de Z . Pero por la propiedad de cobertura de Vitali, uno puede encontrar una bola B  ∈ F que contenga z , contenida en B ( r ), y disjunta de K . Por la propiedad de G , la bola B interseca alguna bola y está contenida en . Pero debido a que K y B son disjuntos, debemos tener i > N. Entonces, para algún i > N, y por lo tanto ${\displaystyle \mathbf {G} _{r}=\{C_{n}\}_{n}}$ ${\displaystyle \mathbf {G} _{r}}$ ${\displaystyle K=\bigcup _{n\leq N}C_{n}}$ ${\displaystyle C_{i}\in \mathbf {G} }$ ${\displaystyle 5C_{i}}$ ${\displaystyle z\in 5C_{i}}$

${\displaystyle Z\subset \bigcup _{n>N}5C_{n}.}$

Esto da para cada N la desigualdad

${\displaystyle \lambda _{d}(Z)\leq \sum _{n>N}\lambda _{d}(5C_{n})=5^{d}\sum _{n>N}\lambda _{d}(C_{n}).}$

Pero como las bolas de están contenidas en B(r+2) , y estas bolas son disjuntas, vemos ${\displaystyle \mathbf {G} _{r}}$

${\displaystyle \sum _{n}\lambda _{d}(C_{n})<\infty .}$

Por lo tanto, el término en el lado derecho de la desigualdad anterior converge a 0 cuando N tiende a infinito, lo que demuestra que Z es despreciable según sea necesario. ^[7]

Espacios de dimensión infinita

El teorema de recubrimiento de Vitali no es válido en entornos de dimensión infinita. El primer resultado en esta dirección fue dado por David Preiss en 1979: ^[8] existe una medida gaussiana γ en un espacio de Hilbert separable (de dimensión infinita) H, de modo que el teorema de recubrimiento de Vitali falla para ( H , Borel( H ),  γ ). Este resultado fue reforzado en 2003 por Jaroslav Tišer: el teorema de recubrimiento de Vitali, de hecho, falla para cada medida gaussiana de dimensión infinita en cualquier espacio de Hilbert separable (de dimensión infinita). ^[9]

Véase también

• Teorema de recubrimiento de Besicovitch

Notas

1. (Vitali 1908).
2. La prueba dada se basa en (Evans y Gariepy 1992, sección 1.5.1)
3. Véase la sección «Del lema de recubrimiento al teorema de recubrimiento» de esta entrada.
4. Véase (Evans y Gariepy 1992).
5. Vitali (1908) permitió un error insignificante.
6. (Halconero 1986).
7. La prueba dada se basa en (Natanson 1955), con algunas anotaciones tomadas de (Evans y Gariepy 1992).
8. (Precio 1979).
9. (Tišer 2003).

Referencias

• Evans, Lawrence C.; Gariepy, Ronald F. (1992), Teoría de la medida y propiedades finas de funciones , Estudios en matemáticas avanzadas, Boca Raton, FL : CRC Press , pp. viii+268, ISBN 0-8493-7157-0, MR  1158660, Zbl  0804.28001
• Falconer, Kenneth J. (1986), La geometría de los conjuntos fractales , Cambridge Tracts in Mathematics, vol. 85, Cambridge: Cambridge University Press , pp. xiv+162, ISBN 0-521-25694-1, MR  0867284, Zbl  0587.28004
• "Teorema de Vitali", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Lebesgue, Henri (1910), "Sur l'intégration des fonctions discontinues", Annales Scientifiques de l'École Normale Supérieure , 27 : 361–450, doi : 10.24033/asens.624 , JFM  41.0457.01
• Natanson, I. P (1955), Teoría de funciones de una variable real , Nueva York: Frederick Ungar Publishing Co., p. 277, señor  0067952, Zbl  0064.29102
• Preiss, David (1979), "Medidas gaussianas y teoremas de cobertura", Commentatione Mathematicae Universitatis Carolinae , 20 (1): 95–99, ISSN  0010-2628, SEÑOR  0526149, Zbl  0386.28015
• Stein, Elias M. ; Shakarchi, Rami (2005), Análisis real. Teoría de la medida, integración y espacios de Hilbert , Princeton Lectures in Analysis, III, Princeton, NJ : Princeton University Press, pp. xx+402, ISBN 0-691-11386-6, MR  2129625, Zbl  1081.28001
• Tišer, Jaroslav (2003), "Teorema de recubrimiento de Vitali en el espacio de Hilbert", Transactions of the American Mathematical Society , 355 (8): 3277–3289 (electrónico), doi : 10.1090/S0002-9947-03-03296-3 , MR  1974687, Zbl  1042.28014
• Vitali, Giuseppe (1908) [17 de diciembre de 1907], "Sui gruppi di punti e sulle funzioni di variabili reali", Atti dell'Accademia delle Scienze di Torino (en italiano), 43 : 75–92, JFM  39.0101.05(Traducción del título) " Sobre grupos de puntos y funciones de variables reales " es el artículo que contiene la primera demostración del teorema de Vitali .