Robust Regression and Outlier Detection es un libro sobre estadística robusta , que se centra especialmente en el punto de ruptura de los métodos de regresión robusta . Fue escrito por Peter Rousseeuw y Annick M. Leroy, y publicado en 1987 por Wiley.
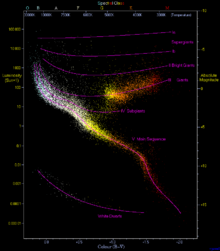
La regresión lineal es el problema de inferir una relación funcional lineal entre una variable dependiente y una o más variables independientes , a partir de conjuntos de datos donde esa relación ha sido oscurecida por el ruido. Los mínimos cuadrados ordinarios suponen que todos los datos se encuentran cerca de la línea o plano de ajuste, pero se alejan de él por la adición de valores residuales distribuidos normalmente . Por el contrario, los métodos de regresión robusta funcionan incluso cuando algunos de los puntos de datos son valores atípicos que no guardan relación con la línea o plano de ajuste, posiblemente porque los datos se extraen de una mezcla de fuentes o posiblemente porque un agente adversario está tratando de corromper los datos para hacer que el método de regresión produzca un resultado inexacto. [1] Una aplicación típica, discutida en el libro, involucra el diagrama de Hertzsprung-Russell de tipos de estrellas, en el que uno desea ajustar una curva a través de la secuencia principal de estrellas sin que el ajuste se vea alterado por las estrellas gigantes y enanas blancas periféricas . [2] El punto de ruptura de un método de regresión robusta es la fracción de datos atípicos que puede tolerar sin dejar de ser preciso. Para este estilo de análisis, es mejor utilizar puntos de ruptura más altos. [1] El punto de ruptura para los mínimos cuadrados ordinarios es cercano a cero (un solo valor atípico puede hacer que el ajuste se aleje arbitrariamente de los datos no corruptos restantes) [2] mientras que otros métodos tienen puntos de ruptura tan altos como el 50%. [1] Aunque estos métodos requieren pocas suposiciones sobre los datos y funcionan bien para datos cuyo ruido no se comprende bien, pueden tener una eficiencia algo menor que los mínimos cuadrados ordinarios (requieren más datos para una precisión de ajuste dada) y su implementación puede ser compleja y lenta. [3]
El libro tiene siete capítulos. [1] [4] El primero es introductorio; describe la regresión lineal simple (en la que solo hay una variable independiente), analiza la posibilidad de valores atípicos que corrompen la variable dependiente o independiente, proporciona ejemplos en los que los valores atípicos producen resultados engañosos, define el punto de ruptura e introduce brevemente varios métodos para la regresión simple robusta, incluida la regresión de mediana repetida . [1] [2] El segundo y tercer capítulos analizan con más detalle el método de mínima mediana de cuadrados para regresión (en el que se busca un ajuste que minimice la mediana de los residuos al cuadrado ) y el método de mínimos cuadrados recortados (en el que se busca minimizar la suma de los residuos al cuadrado que están por debajo de la mediana). Estos dos métodos tienen un punto de ruptura del 50% y se pueden aplicar tanto para la regresión simple (capítulo dos) como para la regresión multivariante (capítulo tres). [1] [5] Aunque la mediana mínima tiene una descripción geométrica atractiva (como encontrar una franja de altura mínima que contenga la mitad de los datos), su baja eficiencia conduce a la recomendación de que se utilicen en su lugar los cuadrados menos recortados; los cuadrados menos recortados también pueden interpretarse como el uso del método de la mediana mínima para encontrar y eliminar valores atípicos y luego usar regresión simple para los datos restantes, [4] y se aproxima a la regresión simple en su eficiencia. [6] Además de describir estos métodos y analizar sus propiedades estadísticas, estos capítulos también describen cómo utilizar el software de los autores para implementar estos métodos. [1] El tercer capítulo también incluye descripciones de algunos estimadores alternativos con altos puntos de ruptura. [7]
El cuarto capítulo describe la estimación unidimensional de un parámetro de ubicación o tendencia central y su implementación en software, y el quinto capítulo profundiza en los algoritmos utilizados por el software para calcular estas estimaciones de manera eficiente. El sexto capítulo trata sobre la detección de valores atípicos , comparando métodos para identificar puntos de datos como valores atípicos basados en estadísticas robustas con otros métodos ampliamente utilizados, y el capítulo final trata sobre problemas de ubicación de dimensiones superiores, así como análisis de series de tiempo y problemas de ajuste de un elipsoide o matriz de covarianza a los datos. [1] [4] [5] [7] Además de utilizar el punto de ruptura para comparar métodos estadísticos, el libro también analiza su equivarianza : ¿para qué familias de transformaciones de datos el ajuste para los datos transformados es igual a la versión transformada del ajuste para los datos originales? [6]
En consonancia con el enfoque de este libro en las aplicaciones, se presentan numerosos ejemplos de análisis realizados con métodos robustos, comparando las estimaciones resultantes con las estimaciones obtenidas con métodos estándar no robustos. [3] [7] Se incluye material teórico, pero se lo ha apartado para que los lectores menos inclinados a la teoría puedan pasarlo por alto fácilmente. Los autores sostienen que los métodos robustos se pueden utilizar tanto para comprobar la aplicabilidad de la regresión ordinaria (cuando los resultados de ambos métodos coinciden) como para sustituirlos en los casos en que los resultados no coinciden. [5]
El libro está dirigido a estadísticos aplicados, con el objetivo de convencerlos de utilizar los métodos robustos que describe. [1] A diferencia de trabajos anteriores en estadística robusta, hace que los métodos robustos sean comprensibles para los profesionales y estén disponibles (a través de su software asociado). [3] No se requieren conocimientos previos de estadística robusta, [4] aunque se supone que se tiene algún conocimiento básico de técnicas estadísticas. [5] El libro también podría utilizarse como libro de texto, [5] aunque el crítico PJ Laycock califica la posibilidad de tal uso de "audaz y progresista" [4] y los críticos Seheult y Green señalan que sería poco probable que un curso de este tipo encajara en los programas de estudio estadísticos británicos. [6]
Los revisores Seheult y Green se quejan de que gran parte del libro actúa como una guía de usuario del software de los autores y debería haberse recortado. [6] Sin embargo, el revisor Gregory F. Piepel escribe que "la presentación es muy buena" y recomienda el libro a cualquier usuario de métodos estadísticos. [1] Y, aunque sugiere la reordenación de algunos materiales, Karen Kafadar recomienda enfáticamente el libro como libro de texto para estudiantes de posgrado y como referencia para profesionales. [5] Y el revisor AC Atkinson resume concisamente el libro como "interesante e importante". [8]
Ha habido varios libros anteriores sobre regresión robusta y detección de valores atípicos, incluidos: [5] [7]
En comparación, Robust Regression and Outlier Detection combina tanto la robustez como la detección de valores atípicos. [5] Es menos teórico, se centra más en los datos y el software, y más centrado en el punto de ruptura que en otras medidas de robustez. [7] Además, es el primero en destacar la importancia del "apalancamiento", el fenómeno por el cual las muestras con valores atípicos de la variable independiente pueden tener una influencia más fuerte en el ajuste que las muestras donde la variable independiente tiene un valor central. [8]