Paridad R

Simetría discreta en ciertos modelos supersimétricos

La paridad R es un concepto de la física de partículas . En el Modelo Estándar Supersimétrico Mínimo , el número bariónico y el número leptónico ya no se conservan mediante todos los acoplamientos renormalizables de la teoría. Dado que la conservación del número bariónico y del número leptónico se ha probado con mucha precisión, estos acoplamientos deben ser muy pequeños para no entrar en conflicto con los datos experimentales. La paridad R es una simetría que actúa sobre los campos del Modelo Estándar Supersimétrico Mínimo (MSSM) que prohíbe estos acoplamientos y se puede definir como ^[1] ${\displaystyle \mathbb {Z} _{2}}$

${\displaystyle P_{\mathrm {R} }=(-1)^{3B+L+2s},}$

o, equivalentemente, como

${\displaystyle P_{\mathrm {R} }=(-1)^{3(B-L)+2s},}$

donde s es el espín , B es el número bariónico y L es el número leptónico. Todas las partículas del Modelo Estándar tienen una paridad R de +1, mientras que las partículas supersimétricas tienen una paridad R de −1.

Téngase en cuenta que existen diferentes formas de paridad con diferentes efectos y principios, no se debe confundir esta paridad con ninguna otra paridad .

Candidato a materia oscura

Con la paridad R preservada, la partícula supersimétrica más ligera ( LSP ) no puede desintegrarse. Esta partícula más ligera (si existe) puede, por lo tanto, explicar la masa faltante observada del universo que generalmente se denomina materia oscura . ^[2] Para ajustar las observaciones, se supone que esta partícula tiene una masa de100  GeV/ c ² a1  TeV/ c ² , es neutro y solo interactúa a través de interacciones débiles e interacciones gravitacionales . A menudo se lo denomina partícula masiva de interacción débil o WIMP.

Por lo general, el candidato a materia oscura del MSSM es una mezcla de los gauginos electrodébiles y los higgsinos y se denomina neutralino . En extensiones del MSSM es posible que un sneutrino sea el candidato a materia oscura. Otra posibilidad es el gravitino , que solo interactúa a través de interacciones gravitacionales y no requiere una estricta paridad R.

Acoplamientos del MSSM que violan la paridad R

Los acoplamientos violadores de paridad R renormalizables del MSSM son

• ${\displaystyle \int d^{2}\theta \;\lambda _{1}\;U^{c}D^{c}D^{c}}$viola B por 1 unidad

La restricción más fuerte que implica este acoplamiento por sí solo proviene de la no observación de oscilaciones neutrón-antineutrón.

• ${\displaystyle \int d^{2}\theta \;\lambda _{2}\;QD^{c}L}$viola L por 1 unidad

La restricción más fuerte que involucra este acoplamiento por sí solo es la violación de la universalidad de la constante de Fermi en las desintegraciones de corrientes cargadas de quarks y leptónicos. ${\displaystyle G_{F}}$

• ${\displaystyle \int d^{2}\theta \;\lambda _{3}\;LE^{c}L}$viola L por 1 unidad

La restricción más fuerte que involucra este acoplamiento solo es la violación de la universalidad de la constante de Fermi en las desintegraciones de corriente cargada leptónica.

• ${\displaystyle \int d^{2}\theta \;\kappa \;LH_{u}}$viola L por 1 unidad

La restricción más fuerte que implica este acoplamiento por sí solo es que conduce a una gran masa de neutrino.

Si bien las restricciones sobre los acoplamientos simples son razonablemente fuertes, si se combinan varios acoplamientos, conducen a la desintegración de protones . Por lo tanto, existen otros límites máximos para los valores de los acoplamientos a partir de los límites máximos para la tasa de desintegración de protones.

Desintegración de protones

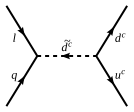
Sin que se conserve el número de bariones y leptones y se tomen acoplamientos para los acoplamientos que violan la paridad R, el protón puede decaer en aproximadamente 10 ⁻²  segundos o, si se supone una violación mínima del sabor, la vida útil del protón se puede extender a 1 año. Dado que se observa que la vida útil del protón es mayor que 10 ³³ a 10 ³⁴  años (dependiendo del canal de desintegración exacto), esto desfavorecería enormemente al modelo. La paridad R establece todos los acoplamientos que violan el número de bariones y leptones renormalizables en cero y el protón es estable en el nivel renormalizable y la vida útil del protón aumenta a 10 ³²  años y es casi consistente con los datos de observación actuales. ${\displaystyle {\mathcal {O}}(1)}$

Debido a que la desintegración de un protón implica la violación simultánea de los números leptónico y bariónico, ningún acoplamiento renormalizable que viole la paridad R conduce a la desintegración de un protón. Esto ha motivado el estudio de la violación de la paridad R, en la que solo un conjunto de acoplamientos que violan la paridad R son distintos de cero, lo que a veces se denomina hipótesis de dominancia de acoplamiento único.

Posibles orígenes de la R-paridad

Una forma muy atractiva de motivar la R-paridad es con una simetría de calibre continua B − L que se rompe espontáneamente a una escala inaccesible para los experimentos actuales. Una continua prohíbe los términos renormalizables que violan B y L . ^{[3] [4] [5] [6]} Si solo se rompe por valores de expectativa de vacío escalares (u otros parámetros de orden) que llevan valores enteros pares de 3( B − L ) , entonces existe un subgrupo remanente discreto exactamente conservado que tiene las propiedades deseadas. ^{[7] [8] [9] [10] [11]} La cuestión crucial es determinar si el sneutrino (el compañero supersimétrico del neutrino), que es impar bajo la R-paridad, desarrolla un valor de expectativa de vacío. Se puede demostrar, sobre bases fenomenológicas, que esto no puede suceder en ninguna teoría donde se rompe a una escala muy por encima de la electrodébil . Esto es cierto en cualquier teoría basada en un mecanismo de balancín a gran escala . ^[12] Como consecuencia, en tales teorías la R-paridad permanece exacta en todas las energías. ${\displaystyle U(1)_{B-L}}$ ${\displaystyle U(1)_{B-L}}$ ${\displaystyle U(1)_{B-L}}$

Este fenómeno puede surgir como una simetría automática en las teorías de gran unificación SO(10) . Esta ocurrencia natural de la paridad R es posible porque en SO(10) los fermiones del Modelo Estándar surgen de la representación de espinores de 16 dimensiones , mientras que el Higgs surge de una representación vectorial de 10 dimensiones. Para hacer un acoplamiento invariante SO(10), uno debe tener un número par de campos de espinores (es decir, hay una paridad de espinores). Después de la ruptura de la simetría GUT, esta paridad de espinores desciende a la paridad R siempre que no se hayan utilizado campos de espinores para romper la simetría GUT. Se han construido ejemplos explícitos de tales teorías SO(10). ^{[13] [14]}

Véase también

• Simetría R

Referencias

1. Martin, SP (6 de septiembre de 2011). "A Supersymmetry Primer". Serie avanzada sobre direcciones en física de alta energía . 18 : 1–98. arXiv : hep-ph/9709356 . doi :10.1142/9789812839657_0001. ISBN . 978-981-02-3553-6.S2CID118973381  .​
2. Jungman, G.; Kamionkowski, M.; Griest, K. (1996). "Materia oscura supersimétrica". Physics Reports . 267 (5–6): 195–373. arXiv : hep-ph/9506380 . Código Bibliográfico :1996PhR...267..195J. doi :10.1016/0370-1573(95)00058-5. S2CID  119067698.
3. Mohapatra, RN (1986). "Nuevas contribuciones a la desintegración doble beta sin neutrinos en teorías supersimétricas". Physical Review D . 34 (11): 3457–3461. Bibcode :1986PhRvD..34.3457M. doi :10.1103/PhysRevD.34.3457. PMID  9957083.
4. Font, A.; Ibáñez, LE; Quevedo, F. (1989). "¿Implica la estabilidad del protón la existencia de un Z0 extra?" (PDF) . Physics Letters B . 228 (1): 79–88. Bibcode :1989PhLB..228...79F. doi :10.1016/0370-2693(89)90529-7.
5. Martin, SP (1992). "Algunos criterios simples para la paridad R calibrada". Physical Review D . 46 (7): R2769–R2772. arXiv : hep-ph/9207218 . Código Bibliográfico :1992PhRvD..46.2769M. doi :10.1103/PhysRevD.46.R2769. PMID  10015267. S2CID  14821065.
6. Martin, SP (1996). "Implicaciones de los modelos supersimétricos con conservación de la paridad R natural". Physical Review D . 54 (3): 2340–2348. arXiv : hep-ph/9602349 . Código Bibliográfico :1996PhRvD..54.2340M. doi :10.1103/PhysRevD.54.2340. PMID  10020912. S2CID  5751474.
7. Fayet, P. (1975). "Extensión invariante de supergauge del mecanismo de Higgs y un modelo para el electrón y su neutrino". Física nuclear B . 90 : 104–124. Código Bibliográfico :1975NuPhB..90..104F. doi :10.1016/0550-3213(75)90636-7.
8. Salam, A.; Strathdee, J. (1975). "Supersimetría y conservación del número fermiónico". Física nuclear B . 87 (1): 85–92. Código Bibliográfico :1975NuPhB..87...85S. doi :10.1016/0550-3213(75)90253-9.
9. Farrar, GR; Weinberg, S. (1983). "Supersimetría a energías ordinarias. II. Invariancia R, bosones de Goldstone y masas de fermiones de calibración". Physical Review D . 27 (11): 2732. Bibcode :1983PhRvD..27.2732F. doi :10.1103/PhysRevD.27.2732.
10. Fayet, P. (1977). "Teorías supersimétricas espontáneamente rotas de interacciones débiles, electromagnéticas y fuertes". Physics Letters B . 69 (4): 489–494. Bibcode :1977PhLB...69..489F. doi :10.1016/0370-2693(77)90852-8.
11. Farrar, GR; Fayet, P. (1978). "Fenomenología de la producción, decaimiento y detección de nuevos estados hadrónicos asociados con la supersimetría". Physics Letters B . 76 (5): 575. Bibcode :1978PhLB...76..575F. doi :10.1016/0370-2693(78)90858-4.
12. Aulakh, CS; Melfo, A.; Rašin, A.; Senjanović, G. (1998). "Supersimetría y simetría izquierda-derecha a gran escala". Physical Review D . 58 (11): 115007. arXiv : hep-ph/9712551 . Código Bibliográfico :1998PhRvD..58k5007A. doi :10.1103/PhysRevD.58.115007. S2CID  43296921.
13. Aulakh, CS; Bajc, B.; Melfo, A.; Rašin, A.; Senjanović, G. (2001). "Teoría SO(10) de R-paridad y masa de neutrino". Física nuclear B . 597 (1–3): 89–109. arXiv : hep-ph/0004031 . Código Bibliográfico :2001NuPhB.597...89A. doi :10.1016/S0550-3213(00)00721-5. S2CID  119100803.
14. Aulakh, CS; Bajc, B.; Melfo, A.; Senjanović, G.; Vissani, F. (2004). "La teoría mínima supersimétrica de gran unificación". Physics Letters B . 588 (3–4): 196–202. arXiv : hep-ph/0306242 . Código Bibliográfico :2004PhLB..588..196A. doi :10.1016/j.physletb.2004.03.031. S2CID  119401374.

Enlaces externos

• Barbier, R.; et al. (2005). "R-paridad violando la supersimetría". Physics Reports . 420 (1–6): 1–195. arXiv : hep-ph/0406039 . Bibcode :2005PhR...420....1B. doi :10.1016/j.physrep.2005.08.006.
• "R-paridad violando ..." xstructure.inr.ac.ru .
• "La paridad R viola..." FNAL . Archivado desde el original el 28 de mayo de 2010.