En mecánica cuántica , un experimento de borrador cuántico es un experimento de interferómetro que demuestra varios aspectos fundamentales de la mecánica cuántica , incluyendo el entrelazamiento cuántico y la complementariedad . [1] [2] : 328 El experimento del borrador cuántico es una variación del clásico experimento de doble rendija de Thomas Young . Establece que cuando se toma una acción para determinar por cuál de las 2 rendijas ha pasado un fotón, el fotón no puede interferir consigo mismo. Cuando una corriente de fotones se marca de esta manera, entonces las franjas de interferencia características del experimento de Young no se verán. El experimento también crea situaciones en las que un fotón que ha sido "marcado" para revelar por qué rendija ha pasado puede ser "desmarcado" más tarde. Un fotón que ha sido "desmarcado" interferirá consigo mismo una vez más, restaurando las franjas características del experimento de Young. [3]
El experimento del borrador cuántico fue propuesto en 1982 por Marlan Scully y Kai Drühl en el artículo Borrador cuántico: un experimento de correlación de fotones propuesto sobre la observación y la "elección retrasada" en la mecánica cuántica , como una forma realizable de probar las predicciones hasta ahora no probadas de la mecánica cuántica. Como inspiraciones, el artículo menciona el enfoque de Eugene Wigner en el problema de la medición , las conversaciones con Willis Lamb y los experimentos mentales de John Archibald Wheeler . El artículo también señala que el experimento podría ejecutarse en modo de elección retrasada , como se conceptualizó en los experimentos mentales de Wheeler, lo que ahora se conoce como un borrador cuántico de elección retrasada . [4]
Este experimento implica un aparato con dos secciones principales. Después de que se crean dos fotones entrelazados , cada uno se dirige a su propia sección del aparato. Cualquier cosa que se haga para conocer la trayectoria del compañero entrelazado del fotón que se está examinando en la parte de doble rendija del aparato influirá en el segundo fotón, y viceversa. La ventaja de manipular los compañeros entrelazados de los fotones en la parte de doble rendija del aparato experimental es que los experimentadores pueden destruir o restaurar el patrón de interferencia en este último sin cambiar nada en esa parte del aparato. Los experimentadores lo hacen manipulando el fotón entrelazado, y pueden hacerlo antes o después de que su compañero haya pasado a través de las rendijas y otros elementos del aparato experimental entre el emisor de fotones y la pantalla de detección. En condiciones en las que la parte de doble rendija del experimento se ha configurado para evitar la aparición de fenómenos de interferencia (porque existe información definitiva sobre "qué trayectoria" sigue), el borrador cuántico se puede utilizar para borrar eficazmente esa información. Al hacerlo, el experimentador restaura la interferencia sin alterar la parte de doble rendija del aparato experimental. [3]
Una variación de este experimento, el borrador cuántico de elección retardada , permite que la decisión de medir o destruir la información de "qué camino" se retrase hasta que la partícula enredada (la que pasa por las rendijas) haya interferido consigo misma o no. [5] En los experimentos de elección retardada, los efectos cuánticos pueden imitar una influencia de acciones futuras sobre eventos pasados. [6] Sin embargo, el orden temporal de las acciones de medición no es relevante. [7]
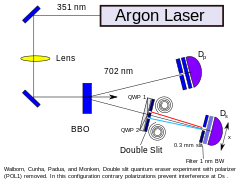
En primer lugar, se dispara un fotón a través de un dispositivo óptico no lineal especializado : un cristal de borato de bario beta (BBO). [3] Este cristal convierte el fotón único en dos fotones entrelazados de menor frecuencia, un proceso conocido como conversión descendente paramétrica espontánea (SPDC). Estos fotones entrelazados siguen caminos separados. Un fotón va directamente a un detector de resolución de polarización, mientras que el segundo fotón pasa a través de la máscara de doble rendija a un segundo detector de resolución de polarización. Ambos detectores están conectados a un circuito de coincidencia , lo que garantiza que solo se cuenten los pares de fotones entrelazados. Un motor paso a paso mueve el segundo detector para escanear el área objetivo, produciendo un mapa de intensidad. Esta configuración produce el patrón de interferencia familiar.
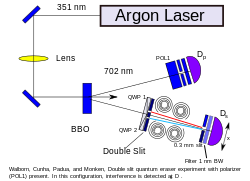
A continuación, se coloca un polarizador circular delante de cada rendija de la máscara de doble rendija, lo que produce una polarización circular en el sentido de las agujas del reloj en la luz que pasa por una rendija y una polarización circular en el sentido contrario de las agujas del reloj en la otra rendija (véase la Figura 1). (La rendija que corresponde a qué polarización depende de la polarización informada por el primer detector). Esta polarización se mide en el segundo detector, "marcando" así los fotones y destruyendo el patrón de interferencia (véase las leyes de Fresnel-Arago ).
Finalmente, se introduce un polarizador lineal en la trayectoria del primer fotón del par entrelazado, lo que le confiere una polarización diagonal (véase la Figura 2). El entrelazamiento garantiza una polarización diagonal complementaria en su compañero, que pasa a través de la máscara de doble rendija. Esto altera el efecto de los polarizadores circulares: cada uno producirá una mezcla de luz polarizada en sentido horario y antihorario. De este modo, el segundo detector ya no puede determinar qué trayectoria se ha tomado y se restauran las franjas de interferencia.
También se puede explicar una doble rendija con polarizadores rotatorios considerando que la luz es una onda clásica. [8] Sin embargo, este experimento utiliza fotones entrelazados, que no son compatibles con la mecánica clásica.
La tecnología de borrado cuántico se puede utilizar para aumentar la resolución de microscopios avanzados . [9]
Un error común sobre este experimento es que puede utilizarse para comunicar información instantáneamente entre dos detectores. [10] Sin embargo, la causalidad simple impide imponer información "dada" sobre los resultados observados. Es importante comprender el papel del detector de coincidencias en esta configuración experimental. El polarizador lineal en la trayectoria superior filtra de manera efectiva la mitad de los fotones entrelazados y, a través del detector de coincidencias, filtra los fotones correspondientes en la trayectoria inferior. El detector de coincidencias solo puede funcionar comparando datos de ambos sensores, lo que hace imposible utilizar esta configuración para la comunicación instantánea.
En otras palabras, sólo un pequeño porcentaje de la luz que pasa a través del cristal BBO se divide en pares entrelazados. La gran mayoría de los fotones que pasan a través del cristal no se dividen y deben eliminarse del conjunto de datos final como ruido no deseado. Dado que no hay forma de que los detectores midan si un fotón ha sido o no parte de un par entrelazado, esa decisión se toma observando el tiempo y filtrando cualquier fotón que no se capte al mismo tiempo que su "gemelo" en el otro detector. Por lo tanto, cuando se crea un par de fotones entrelazados, pero uno de los dos es bloqueado por un polarizador y se pierde, el fotón restante se filtrará del conjunto de datos como si fuera uno de los muchos fotones no entrelazados. Cuando se ve de esta manera, no es sorprendente que hacer cambios en la ruta superior pueda tener un impacto en las mediciones tomadas en la ruta inferior, ya que las dos mediciones se comparan y se utilizan para filtrar los datos.
Tenga en cuenta que en el estado final de esta configuración experimental, las mediciones en la ruta inferior siempre muestran un patrón borroso en los datos sin procesar. Solo es posible ver un patrón de interferencia filtrando los datos con el detector de coincidencia y observando solo los fotones que eran la mitad de un par entrelazado.