AND-OR-invertir

La lógica AND-OR-invertida (AOI) y las puertas AOI son funciones lógicas compuestas (o complejas) de dos niveles construidas a partir de la combinación de una o más puertas AND seguidas de una puerta NOR (equivalente a una puerta OR a través de una puerta Inversora , que es la parte "OI" de "AOI"). La construcción de celdas AOI es particularmente eficiente utilizando tecnología CMOS , donde la cantidad total de puertas de transistores se puede comparar con la misma construcción utilizando lógica NAND o lógica NOR . El complemento de la lógica AOI es la lógica OR-AND-invertida (OAI), donde las puertas OR preceden a una puerta NAND. ^[1]

Descripción general

La mayoría de las optimizaciones lógicas dan como resultado una expresión lógica de suma de productos o de producto de sumas. ^[2]

AOI se utiliza para la suma de productos, las variables se combinan mediante AND para formar mintérminos que luego se invierten mediante OR, como:

• AB + C    se conoce como una puerta AOI 2-1.
• AB + CD    se conoce como una puerta AOI 2-2. ^[3]
• ABC + DEF    se conoce como una puerta AOI 3-3. ^[4]
• ABCD + EFGH    se conoce como una puerta AOI 4-4. ^[5]
• ABCDE + FGH + JK    se conoce como una puerta AOI 4-3-2.
• y otras variaciones.

Ejemplos

Las puertas AOI realizan una o más operaciones AND seguidas de una operación OR y luego una inversión.

Puerta AOI 2-1

Símbolo de la puerta AOI 2-1. La puerta AND tiene entradas A y B (según la tabla).

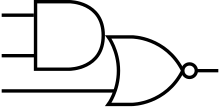
La puerta AOI 2-1 se puede representar mediante la siguiente ecuación booleana y tabla de verdad :

${\displaystyle Q={\overline {(A\wedge B)\vee C}}.}$

Puerta AOI 2-2

Símbolo de la puerta AOI 2-2

Se encuentran ejemplos del mundo real de una puerta AOI 2-2 en los circuitos integrados lógicos CD4085B, SN74LS51, SN5450 (ver más abajo). ^{[3] [4] [6]}

La puerta AOI 2-2 se puede representar mediante la siguiente ecuación booleana y tabla de verdad :

${\displaystyle Q={\overline {(A\wedge B)\vee (C\wedge D)}}.}$

Puerta AOI 3-3

Se encuentran ejemplos del mundo real de una puerta AOI 3-3 en el CI lógico SN74LS51 (ver más abajo). ^[4]

La puerta AOI 3-3 se puede representar mediante la siguiente ecuación booleana y tabla de verdad :

${\displaystyle Q={\overline {(A\wedge B\wedge C)\vee (D\wedge E\wedge F)}}.}$

Su tabla lógica tendría 64 entradas, pero no se muestra.

Puerta AOI 4-4

Símbolo de la puerta AOI 4-4

Se encuentran ejemplos del mundo real de una puerta AOI 4-4 en el CI lógico CD4048B (ver más abajo). ^[5]

La puerta AOI 4-4 se puede representar mediante la siguiente ecuación booleana y tabla de verdad :

${\displaystyle Q={\overline {(A\wedge B\wedge C\wedge D)\vee (E\wedge F\wedge G\wedge H)}}.}$

Su tabla lógica tendría 256 entradas, pero no se muestra.

Extensiones a múltiples niveles

Es posible crear puertas compuestas de varios niveles, que combinan la lógica de las puertas AND-OR-Invert con las puertas OR-AND-Invert . ^[7] A continuación se muestra un ejemplo. Las partes que implementan la misma lógica se han colocado en cuadros con el mismo color.

puerta lógica compuesta para (CD + B) A , más versión CMOS.

Implementación electrónica

Una puerta lógica AOI21 en CMOS que utiliza una puerta compleja (izquierda) y puertas estándar (derecha)

Las puertas AND-OR-invert (AOI) y OAI se pueden implementar fácilmente en circuitos CMOS . Las puertas AOI tienen la ventaja particular de que la cantidad total de transistores (o puertas) es menor que si las funciones AND, NOT y OR se implementaran por separado. Esto da como resultado mayor velocidad, menor consumo de energía, menor área y un costo de fabricación potencialmente menor. Por ejemplo, una puerta AOI 2-1 se puede construir con 6 transistores en CMOS, en comparación con 10 transistores utilizando una puerta NAND de 2 entradas (4 transistores), un inversor (2 transistores) y una puerta NOR de 2 entradas (4 transistores).

En la lógica NMOS , la mitad inferior del circuito CMOS se utiliza en combinación con un dispositivo de carga o un transistor pull-up (normalmente una carga de agotamiento o una carga dinámica ).

Las puertas AOI son igualmente eficientes en la lógica transistor-transistor (TTL).

Ejemplos

Familia lógica de la serie CMOS 4000 :

• CD4085B = puerta AOI dual 2-2 ^[3]
• CD4086B = puerta AOI 2-2-2-2 expandible única" ^[8]
• CD4048B = 8 entradas y 8 funciones expandibles con salida de tres estados , 8 opciones para el tipo de compuerta: 8 NOR / 8 OR / 8 NAND / 8 AND / 4-4 AND-OR-Invertir / 4-4 AND-OR / 4-4 OR-AND-Invertir / 4-4 OR-AND ^[5]

Familia lógica de la serie TTL 7400 : (en décadas pasadas, había varias piezas AOI disponibles en la familia 7400, pero actualmente la mayoría están obsoletas (ya no se fabrican))

• SN5450 = puerta AOI dual 2-2, una es expandible ^[6] (SN54 es la versión militar de SN74)
• SN74LS51 = puerta AOI 2-2 y puerta AOI 3-3 ^[4]
• SN54LS54 = puerta AOI única 2-3-3-2 ^[9]

• 
  El esquema del CI SN74LS51 consta de una puerta AOI 3-3 y una puerta AOI 2-2 ^[4]
• 
  Distribución de pines del CI SN74LS51 ^[4]

Véase también

• Lista de circuitos integrados de la serie 7400
• Lista de circuitos integrados de la serie 4000

Referencias

1. Producto de reducción de sumas utilizando el mapa de Karnaugh.
2. Suma del producto (SOP) y producto de la suma (POS).
3. "Hoja de datos del CD4085B". Texas Instruments . 2003. Archivado (PDF) del original el 5 de marzo de 2019.
4. «Hoja de datos del SN74LS51». Texas Instruments . 1988. Archivado (PDF) del original el 30 de noviembre de 2020.
5. "Hoja de datos del CD4048B". Texas Instruments . 2003. Archivado (PDF) del original el 5 de marzo de 2019.
6. "Hoja de datos del SN5450". Texas Instruments . 1988. Archivado (PDF) del original el 26 de julio de 2018.
7. Fischer, P. "Aussagenlogik und Gatter" (PDF) . Universidad de Heidelberg . Consultado el 21 de enero de 2024 .
8. "Hoja de datos del CD4086B". Texas Instruments . 2003. Archivado (PDF) del original el 15 de abril de 2019.
9. "Ficha técnica del SN54LS54". Texas Instruments . 1988. Archivado (PDF) del original el 5 de marzo de 2018.

• Tinder, Richard F. (2000). Diseño digital de ingeniería: segunda edición revisada. Págs. 317–319. ISBN 0-12-691295-5. Consultado el 4 de julio de 2008 .
• John, Michael (1997). Circuitos integrados específicos de la aplicación . Consultado el 4 de julio de 2008 .