

En geometría elemental , el teorema de la pizza establece la igualdad de dos áreas que surgen cuando se divide un disco de una determinada manera.
El teorema se llama así porque imita una técnica tradicional de corte de pizza . Muestra que si dos personas comparten una pizza cortada en 8 trozos (o cualquier múltiplo de 4 mayor que 8) y toman porciones alternadas, cada uno recibirá una cantidad igual de pizza, independientemente del punto de corte central.
Sea p un punto interior del disco, y sea n un múltiplo de 4 que sea mayor o igual a 8. Forme n sectores del disco con ángulos iguales eligiendo una línea arbitraria a través de p , rotando la línea norte/2 − 1 veces en un ángulo de 2π/norte radianes , y cortando el disco en cada uno de los resultantesnorte/2 líneas. Numera los sectores consecutivamente en sentido horario o antihorario. Entonces el teorema de la pizza establece que:
El teorema de la pizza fue propuesto originalmente como un problema de desafío por Upton (1967). La solución publicada a este problema, por Michael Goldberg, implicó la manipulación directa de las expresiones algebraicas para las áreas de los sectores. Carter y Wagon (1994a) proporcionan una prueba alternativa por disección . Muestran cómo dividir los sectores en partes más pequeñas de modo que cada pieza en un sector de número impar tenga una pieza congruente en un sector de número par, y viceversa. Frederickson (2012) proporcionó una familia de pruebas de disección para todos los casos (en los que el número de sectores es 8, 12, 16, ... ).
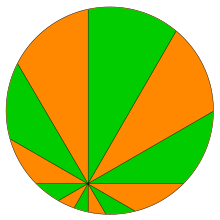
El requisito de que el número de sectores sea múltiplo de cuatro es necesario: como demostró Don Coppersmith , dividir un disco en cuatro sectores, o un número de sectores que no sea divisible por cuatro, en general no produce áreas iguales. Mabry y Deiermann (2009) respondieron a un problema de Carter y Wagon (1994b) proporcionando una versión más precisa del teorema que determina cuál de los dos conjuntos de sectores tiene mayor área en los casos en que las áreas son desiguales. Específicamente, si el número de sectores es 2 ( mod 8) y ninguna rebanada pasa por el centro del disco, entonces el subconjunto de rebanadas que contiene el centro tiene un área menor que el otro subconjunto, mientras que si el número de sectores es 6 (mod 8) y ninguna rebanada pasa por el centro, entonces el subconjunto de rebanadas que contiene el centro tiene un área mayor. Un número impar de sectores no es posible con cortes en línea recta, y una rebanada a través del centro hace que los dos subconjuntos sean iguales independientemente del número de sectores.
Mabry y Deiermann (2009) también observan que, cuando la pizza se divide de manera uniforme, también lo hace su corteza (la corteza puede interpretarse como el perímetro del disco o el área entre el límite del disco y un círculo más pequeño que tiene el mismo centro, con el punto de corte en el interior de este último), y dado que los discos delimitados por ambos círculos se dividen de manera uniforme, también lo hace su diferencia. Sin embargo, cuando la pizza se divide de manera desigual, el comensal que obtiene la mayor área de pizza en realidad obtiene la menor corteza.
Como señalan Hirschhorn et al. (1999), una división igual de la pizza también conduce a una división igual de sus ingredientes, siempre que cada ingrediente se distribuya en un disco (no necesariamente concéntrico con toda la pizza) que contenga el punto central p de la división en sectores.
Hirschhorn et al. (1999) demuestran que una pizza cortada de la misma manera que el teorema de la pizza, en un número n de sectores con ángulos iguales donde n es divisible por cuatro, también puede ser compartida equitativamente entre n /4 personas. Por ejemplo, una pizza dividida en 12 sectores puede ser compartida equitativamente por tres personas así como por dos; sin embargo, para dar cabida a los cinco Hirschhorn, una pizza necesitaría ser dividida en 20 sectores.
Cibulka et al. (2010) y Knauer, Micek & Ueckerdt (2011) estudian la teoría de juegos de elección de porciones de pizza gratis para garantizar una gran porción, un problema planteado por Dan Brown y Peter Winkler . En la versión del problema que estudian, una pizza se corta radialmente (sin la garantía de sectores de ángulos iguales) y dos comensales eligen alternativamente porciones de pizza que están adyacentes a un sector ya comido. Si los dos comensales intentan maximizar la cantidad de pizza que comen, el comensal que toma la primera porción puede garantizar una porción de 4/9 de la pizza total, y existe un corte de la pizza tal que no puede tomar más. El problema de la división justa o del corte de la torta considera juegos similares en los que diferentes jugadores tienen diferentes criterios para medir el tamaño de su porción; por ejemplo, un comensal puede preferir obtener la mayor cantidad de pepperoni mientras que otro comensal puede preferir obtener la mayor cantidad de queso.
Brailov (2021), Brailov (2022), Ehrenborg, Morel y Readdy (2022) y Ehrenborg, Morel y Readdy (2023) extienden este resultado a dimensiones superiores, es decir, para ciertas disposiciones de hiperplanos, la suma alternada de volúmenes recortados por los hiperplanos es cero.
Compárese con el teorema del sándwich de jamón , un resultado sobre el corte de objetos n -dimensionales. La versión bidimensional implica que cualquier pizza, sin importar lo deforme que sea, puede tener su área y la longitud de su corteza divididas simultáneamente por un solo corte en línea recta cuidadosamente elegido. La versión tridimensional implica la existencia de un corte plano que comparte por igual la base, el tomate y el queso.
{{citation}}: Mantenimiento de CS1: postscript ( enlace ).{{citation}}: Mantenimiento de CS1: postscript ( enlace ).