En astrofísica , la relación de Phillips es la relación entre la luminosidad máxima de una supernova de tipo Ia y la velocidad de evolución de la luminosidad después del máximo de luz. La relación fue descubierta independientemente por el estadístico y astrónomo estadounidense Bert Woodard Rust y el astrónomo soviético Yury Pavlovich Pskovskii en la década de 1970. [1] [2] [3] Encontraron que cuanto más rápido se desvanecía la supernova desde el máximo de luz, más débil era su magnitud máxima. Como parámetro principal que caracteriza la forma de la curva de luz, Pskovskii utilizó β, la tasa media de disminución del brillo fotográfico desde el máximo de luz hasta el punto en el que cambia la tasa de disminución de la luminosidad. β se mide en magnitudes por intervalos de 100 días. [4] La selección de este parámetro se justifica por el hecho de que, en ese momento, la probabilidad de descubrir una supernova antes del máximo de luz y obtener la curva de luz completa era pequeña. Además, las curvas de luz existentes estaban en su mayoría incompletas. Por otra parte, determinar la disminución después del máximo de luz fue bastante simple para la mayoría de las supernovas observadas.
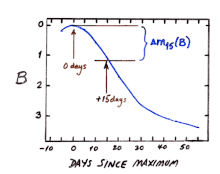
A principios de los años 1980 aparecieron las cámaras CCD y el número de descubrimientos de supernovas aumentó sustancialmente. Además, también aumentó la probabilidad de descubrir supernovas antes de que alcanzaran su luz máxima y de seguir su evolución de brillo durante más tiempo. Las primeras curvas de luz de las supernovas Ia obtenidas mediante fotometría CCD mostraron que algunas supernovas tenían tasas de declive más rápidas que otras. Más tarde, se descubrió la SN Ia 1991bg, de baja luminosidad y con una tasa de declive rápida. Todo esto motivó al astrónomo estadounidense Mark M. Phillips a revisar esta relación precisamente durante el curso del Calán/Tololo Supernova Survey . [5] La correlación había sido difícil de probar porque el parámetro de la pendiente de Pskovskii (β) era difícil de medir con precisión en la práctica, una condición necesaria para probar la correlación. En lugar de tratar de determinar la pendiente, Phillips utilizó un procedimiento más simple y robusto que consistía en "medir la cantidad total en magnitudes que la curva de luz decae desde su brillo máximo durante un período específico después de la luz máxima". Se definió como la disminución de la curva de luz de magnitud B desde la luz máxima hasta la magnitud 15 días después del máximo B , un parámetro que él llamó . La oración principal de la sección de agradecimientos del artículo de Phillips dice: "Estoy en deuda con George Jacoby por sugerir el parámetro como una alternativa a la β de Pskovskii". La relación establece que la magnitud máxima intrínseca de la banda B está dada por
[6]
Phillips dedicó el artículo de la revista que confirma la correlación propuesta por Yuri Pskovskii con Pskovskii, quien murió unas semanas después de que se publicara la evidencia de Phillips que confirmaba la relación.
Se ha reformulado para incluir la evolución en múltiples bandas fotométricas, con una pendiente significativamente más superficial [7] [8] y como un estiramiento en el eje del tiempo en relación con una plantilla estándar. [9] La relación se utiliza normalmente para llevar cualquier magnitud de pico de supernova de tipo Ia a un valor de vela estándar .