En geometría , un miriágono o 10000-gono es un polígono con 10000 lados. Varios filósofos han utilizado el miriágono regular para ilustrar cuestiones relacionadas con el pensamiento. [1] [2] [3] [4] [5]
Un miriágono regular se representa mediante el símbolo de Schläfli {10 000} y se puede construir como un 5000-gono truncado , t{5000}, o un 2500-gono truncado dos veces, tt{2500}, o un 1250-gono truncado tres veces, ttt{1250}, o un 625-gono truncado cuádruplemente, tttt{625}.
La medida de cada ángulo interno de un miriágono regular es 179,964°. El área de un miriágono regular con lados de longitud a está dada por
El resultado difiere del área de su círculo circunscrito en hasta 40 partes por mil millones .
Como 10.000 = 2 4 × 5 4 , el número de lados no es un producto de primos de Fermat distintos ni una potencia de dos. Por lo tanto, el miriágono regular no es un polígono construible . De hecho, ni siquiera es construible con el uso de un trisector de ángulos, ya que el número de lados no es un producto de primos de Pierpont distintos ni un producto de potencias de dos y tres.
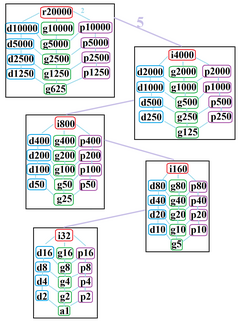
El miriágono regular tiene simetría diedral Dih 10000 , orden 20000, representada por 10000 líneas de reflexión. Dih 10000 tiene 24 subgrupos diédricos: (Dih 5000 , Dih 2500 , Dih 1250 , Dih 625 ), (Dih 2000 , Dih 1000 , Dih 500 , Dih 250 , Dih 125 ), (Dih 400 , Dih 200 , Dih 100 , Dih 50 , Dih 25 ), (Dih 80 , Dih 40 , Dih 20 , Dih 10 , Dih 5 ) y (Dih 16 , Dih 8 , Dih 4 , Dih 2 , Dih 1 ). También tiene 25 simetrías cíclicas más como subgrupos: (Z 10000 , Z 5000 , Z 2500 , Z 1250 , Z 625 ), (Z 2000 , Z 1000 , Z 500 , Z 250 , Z 125 ), (Z 400 , Z 200 , Z 100 , Z 50 , Z 25 ), (Z 80 , Z 40 , Z 20 , Z 10 ), y (Z 16 , Z 8 , Z 4 , Z 2 , Z 1 ), donde Z n representa una simetría rotacional de π / n radianes.
John Conway etiqueta estas simetrías inferiores con una letra y el orden de la simetría sigue a la letra. [6] r20000 representa simetría completa y a1 etiqueta ausencia de simetría. Da d (diagonal) con líneas simétricas a través de vértices, p con líneas simétricas a través de aristas (perpendicular), i con líneas simétricas a través de vértices y aristas, y g para simetría rotacional.
Estas simetrías inferiores permiten grados de libertad para definir miriágonos irregulares. Solo el subgrupo g10000 no tiene grados de libertad, pero puede verse como aristas dirigidas .
Un miriagrama es un polígono en estrella de 10.000 lados . Existen 1999 formas regulares [a] dadas por los símbolos de Schläfli de la forma {10000/ n }, donde n es un número entero entre 2 y 5.000 que es coprimo con 10.000. También existen 3000 figuras en estrella regulares en los casos restantes.
En la novela Flatland , se supone que el Círculo Principal tiene diez mil lados, lo que lo convierte en un miriágono.