En física y química , la serie de Lyman es una serie espectral de transiciones del hidrógeno y las líneas de emisión ultravioleta resultantes del átomo de hidrógeno cuando un electrón pasa de n ≥ 2 a n = 1 (donde n es el número cuántico principal ), el nivel de energía más bajo del electrón (estado fundamental). Las transiciones se nombran secuencialmente con letras griegas : de n = 2 a n = 1 se llama Lyman-alfa , de 3 a 1 es Lyman-beta, de 4 a 1 es Lyman-gamma, y así sucesivamente. La serie recibe su nombre de su descubridor, Theodore Lyman . Cuanto mayor sea la diferencia en los números cuánticos principales, mayor será la energía de la emisión electromagnética.
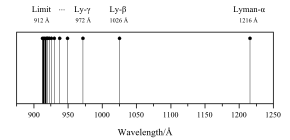
La primera línea del espectro de la serie de Lyman fue descubierta en 1906 por el físico Theodore Lyman IV, que estudiaba el espectro ultravioleta del gas hidrógeno excitado eléctricamente. El resto de las líneas del espectro (todas en el ultravioleta) fueron descubiertas por Lyman entre 1906 y 1914. El espectro de la radiación emitida por el hidrógeno no es continuo ni discreto. A continuación se muestra una ilustración de la primera serie de líneas de emisión del hidrógeno:
Históricamente, explicar la naturaleza del espectro del hidrógeno fue un problema considerable en física . Nadie pudo predecir las longitudes de onda de las líneas de hidrógeno hasta 1885, cuando la fórmula de Balmer proporcionó una fórmula empírica para el espectro del hidrógeno visible. En cinco años, Johannes Rydberg ideó una fórmula empírica que resolvió el problema, presentada por primera vez en 1888 y en su forma final en 1890. Rydberg logró encontrar una fórmula que coincidiera con las líneas de emisión de la serie de Balmer conocidas , y también predijo las aún no descubiertas. Se encontraron diferentes versiones de la fórmula de Rydberg con diferentes números simples para generar diferentes series de líneas.
El 1 de diciembre de 2011 se anunció que la Voyager 1 había detectado la primera radiación Lyman-alfa procedente de la Vía Láctea . La radiación Lyman-alfa ya se había detectado en otras galaxias, pero debido a la interferencia del Sol, la radiación procedente de la Vía Láctea no era detectable. [1]
La versión de la fórmula de Rydberg que generó la serie de Lyman fue: [2] donde n es un número natural mayor o igual a 2 (es decir, n = 2, 3, 4, ... ).
Por lo tanto, las líneas que se ven en la imagen superior son las longitudes de onda correspondientes a n = 2 a la derecha, y a n → ∞ a la izquierda. Hay infinitas líneas espectrales, pero se vuelven muy densas a medida que se acercan a n → ∞ (el límite de Lyman ), por lo que solo aparecen algunas de las primeras líneas y la última.
Las longitudes de onda de la serie Lyman son todas ultravioletas:
En 1914, cuando Niels Bohr elaboró su teoría del modelo de Bohr , se explicó la razón por la que las líneas espectrales del hidrógeno se ajustaban a la fórmula de Rydberg. Bohr descubrió que el electrón ligado al átomo de hidrógeno debe tener niveles de energía cuantizados descritos por la siguiente fórmula:
Según el tercer supuesto de Bohr, siempre que un electrón cae desde un nivel de energía inicial E i a un nivel de energía final E f , el átomo debe emitir radiación con una longitud de onda de
También existe una notación más cómoda cuando se trata de energía en unidades de electronvoltios y longitudes de onda en unidades de angstroms .
Reemplazando la energía en la fórmula anterior por la expresión de la energía en el átomo de hidrógeno donde la energía inicial corresponde al nivel de energía n y la energía final corresponde al nivel de energía m ,
Donde R H es la misma constante de Rydberg para el hidrógeno de la conocida fórmula de Rydberg. Esto también significa que la inversa de la constante de Rydberg es igual al límite de Lyman.
Para la conexión entre Bohr, Rydberg y Lyman, se debe reemplazar m por 1 para obtener
que es la fórmula de Rydberg para la serie de Lyman. Por lo tanto, cada longitud de onda de las líneas de emisión corresponde a un electrón que cae desde un cierto nivel de energía (mayor que 1) al primer nivel de energía.