
Un pozo de potencial es la región que rodea un mínimo local de energía potencial . La energía capturada en un pozo de potencial no puede convertirse en otro tipo de energía ( energía cinética en el caso de un pozo de potencial gravitacional ) porque está capturada en el mínimo local de un pozo de potencial. Por lo tanto, un cuerpo no puede avanzar hasta el mínimo global de energía potencial, como tendería naturalmente a hacer debido a la entropía .
Se puede liberar energía de un pozo de potencial si se agrega suficiente energía al sistema de modo que se supere el máximo local. En física cuántica , la energía potencial puede escapar de un pozo de potencial sin energía adicional debido a las características probabilísticas de las partículas cuánticas ; en estos casos, se puede imaginar que una partícula atraviesa las paredes de un pozo de potencial.
El gráfico de una función de energía potencial en 2D es una superficie de energía potencial que se puede imaginar como la superficie de la Tierra en un paisaje de colinas y valles. Entonces, un pozo de potencial sería un valle rodeado por todos lados con terreno más alto, que así podría llenarse de agua (por ejemplo, ser un lago ) sin que el agua fluya hacia otro mínimo más bajo (por ejemplo, el nivel del mar ).
En el caso de la gravedad , la región alrededor de una masa es un pozo de potencial gravitacional, a menos que la densidad de la masa sea tan baja que las fuerzas de marea de otras masas sean mayores que la gravedad del propio cuerpo.
Una colina potencial es lo opuesto a un pozo potencial y es la región que rodea un máximo local .

El confinamiento cuántico se puede observar una vez que el diámetro de un material es de la misma magnitud que la longitud de onda de De Broglie de la función de onda del electrón . [1] Cuando los materiales son tan pequeños, sus propiedades electrónicas y ópticas se desvían sustancialmente de las de los materiales a granel. [2]
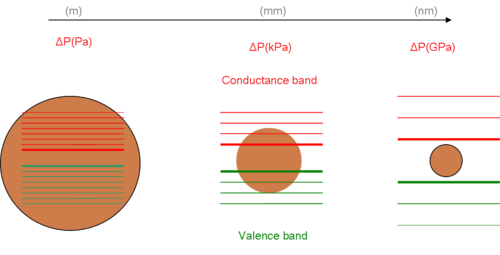
Una partícula se comporta como si fuera libre cuando la dimensión de confinamiento es grande en comparación con la longitud de onda de la partícula. Durante este estado, la banda prohibida permanece en su energía original debido a un estado de energía continua. Sin embargo, a medida que la dimensión de confinamiento disminuye y alcanza un cierto límite, típicamente en la nanoescala, el espectro de energía se vuelve discreto . Como resultado, la banda prohibida se vuelve dependiente del tamaño. A medida que el tamaño de las partículas disminuye, los electrones y los huecos de electrones se acercan, y la energía necesaria para activarlos aumenta, lo que finalmente resulta en un desplazamiento hacia el azul en la emisión de luz .
En concreto, el efecto describe el fenómeno que resulta de la compresión de electrones y huecos de electrones hasta una dimensión que se aproxima a una medida cuántica crítica, denominada radio de Bohr del excitón . En la aplicación actual, un punto cuántico , como una esfera pequeña, se limita en tres dimensiones, un cable cuántico se limita en dos dimensiones y un pozo cuántico se limita sólo en una dimensión. Estos también se conocen como pozos de potencial de dimensión cero, unidimensional y bidimensional, respectivamente. En estos casos se refieren al número de dimensiones en las que una partícula confinada puede actuar como portador libre. Consulte los enlaces externos, a continuación, para ver ejemplos de aplicación en biotecnología y tecnología de células solares.
Las propiedades electrónicas y ópticas de los materiales se ven afectadas por el tamaño y la forma. Los logros técnicos bien establecidos, incluidos los puntos cuánticos, se derivaron de la manipulación del tamaño y la investigación para su corroboración teórica sobre el efecto de confinamiento cuántico. [3] La parte principal de la teoría es que el comportamiento del excitón se asemeja al de un átomo a medida que el espacio que lo rodea se acorta. Una aproximación bastante buena del comportamiento de un excitón es el modelo 3-D de una partícula en una caja . [4] La solución de este problema proporciona una única [ aclaración necesaria ] conexión matemática entre los estados de energía y la dimensión del espacio. Al disminuir el volumen o las dimensiones del espacio disponible, aumenta la energía de los estados. En el diagrama se muestra el cambio en el nivel de energía del electrón y la brecha de banda entre el nanomaterial y su estado en masa.
La siguiente ecuación muestra la relación entre el nivel de energía y el espaciado dimensional:
Los resultados de la investigación [5] proporcionan una explicación alternativa del cambio de propiedades a escala nanométrica. En la fase masiva, las superficies parecen controlar algunas de las propiedades observadas macroscópicamente. Sin embargo, en las nanopartículas , las moléculas de la superficie no obedecen a la configuración esperada [ ¿cuál? ] en el espacio. Como resultado, la tensión superficial cambia enormemente.
La ecuación de Young-Laplace puede proporcionar una base para la investigación de la escala de fuerzas aplicadas a las moléculas de la superficie:
Suponiendo que la partícula tiene forma esférica y resolviendo la ecuación de Young-Laplace para los nuevos radios (nm), estimamos el nuevo GPa. Cuanto más pequeños sean los radios, mayor será la presión presente. El aumento de la presión a escala nanométrica genera fuerzas intensas hacia el interior de la partícula. En consecuencia, la estructura molecular de la partícula parece ser diferente de la estructura general, especialmente en la superficie. Estas anomalías en la superficie son responsables de los cambios en las interacciones interatómicas y en la brecha de banda . [6] [7]