La regresión segmentada , también conocida como regresión por partes o regresión de barras quebradas , es un método de análisis de regresión en el que la variable independiente se divide en intervalos y se ajusta un segmento de línea separado a cada intervalo. El análisis de regresión segmentada también se puede realizar en datos multivariados mediante la división de las distintas variables independientes. La regresión segmentada es útil cuando las variables independientes, agrupadas en diferentes grupos, exhiben diferentes relaciones entre las variables en estas regiones. Los límites entre los segmentos son puntos de ruptura .
La regresión lineal segmentada es una regresión segmentada mediante la cual las relaciones en los intervalos se obtienen mediante regresión lineal .
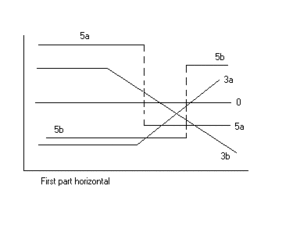


La regresión lineal segmentada con dos segmentos separados por un punto de corte puede ser útil para cuantificar un cambio abrupto de la función de respuesta (Yr) de un factor influyente variable ( x ). El punto de corte puede interpretarse como un valor crítico , seguro o umbral más allá o por debajo del cual se producen efectos (no) deseados. El punto de corte puede ser importante en la toma de decisiones [1]
Las figuras ilustran algunos de los resultados y tipos de regresión obtenibles.
Un análisis de regresión segmentada se basa en la presencia de un conjunto de datos ( y, x ), en el que y es la variable dependiente y x la variable independiente .
El método de mínimos cuadrados aplicado por separado a cada segmento, mediante el cual las dos líneas de regresión se ajustan al conjunto de datos lo más cerca posible mientras se minimiza la suma de cuadrados de las diferencias (SSD) entre los valores observados ( y ) y calculados (Yr) de la variable dependiente, da como resultado las dos ecuaciones siguientes:
dónde:
Los datos pueden mostrar muchos tipos o tendencias, [2] véanse las figuras.
El método también produce dos coeficientes de correlación (R):
y
dónde:
y
En la determinación de la tendencia más adecuada, se deben realizar pruebas estadísticas para garantizar que dicha tendencia sea confiable (significativa).
Cuando no se puede detectar ningún punto de interrupción significativo, se debe recurrir a una regresión sin punto de interrupción.

Para la figura azul de la derecha que da la relación entre el rendimiento de mostaza (Yr = Ym, t/ha) y la salinidad del suelo ( x = Ss, expresada como conductividad eléctrica de la solución del suelo CE en dS/m) se encuentra que: [3]
BP = 4,93, A 1 = 0, K 1 = 1,74, A 2 = −0,129, K 2 = 2,38, R 1 2 = 0,0035 (insignificante), R 2 2 = 0,395 (significativo) y:
lo que indica que las salinidades del suelo < 4,93 dS/m son seguras y las salinidades del suelo > 4,93 dS/m reducen el rendimiento a 0,129 t/ha por unidad de aumento de la salinidad del suelo.
La figura también muestra los intervalos de confianza y la incertidumbre según se detalla a continuación.

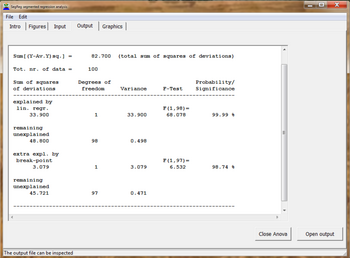
Las siguientes pruebas estadísticas se utilizan para determinar el tipo de tendencia:
Además, se utiliza el coeficiente de correlación de todos los datos (Ra), el coeficiente de determinación o coeficiente de explicación, los intervalos de confianza de las funciones de regresión y el análisis ANOVA . [5]
El coeficiente de determinación para todos los datos (Cd), que debe maximizarse en las condiciones establecidas por las pruebas de significancia, se obtiene a partir de:
donde Yr es el valor esperado (predicho) de y según las ecuaciones de regresión anteriores y Ya es el promedio de todos los valores de y .
El coeficiente de Cd varía entre 0 (ninguna explicación) y 1 (explicación completa, coincidencia perfecta).
En una regresión lineal pura, no segmentada, los valores de Cd y Ra 2 son iguales. En una regresión segmentada, Cd debe ser significativamente mayor que Ra 2 para justificar la segmentación.
El valor óptimo del punto de ruptura se puede encontrar de manera que el coeficiente Cd sea máximo .

La regresión segmentada se utiliza a menudo para detectar en qué rango una variable explicativa (X) no tiene efecto sobre la variable dependiente (Y), mientras que más allá del alcance hay una respuesta clara, ya sea positiva o negativa. El alcance de ningún efecto puede encontrarse en la parte inicial del dominio X o, por el contrario, en su última parte. Para el análisis de "ningún efecto", la aplicación del método de mínimos cuadrados para el análisis de regresión segmentada [6] puede no ser la técnica más apropiada porque el objetivo es más bien encontrar el tramo más largo en el que se puede considerar que la relación YX posee pendiente cero mientras que más allá del alcance la pendiente es significativamente diferente de cero pero el conocimiento sobre el mejor valor de esta pendiente no es material. El método para encontrar el rango de ningún efecto es la regresión parcial progresiva [7] sobre el rango, extendiendo el rango con pequeños pasos hasta que el coeficiente de regresión se vuelve significativamente diferente de cero.
En la siguiente figura, el punto de quiebre se encuentra en X=7,9, mientras que para los mismos datos (véase la figura azul anterior para el rendimiento de mostaza), el método de mínimos cuadrados arroja un punto de quiebre solo en X=4,9. El último valor es menor, pero el ajuste de los datos más allá del punto de quiebre es mejor. Por lo tanto, dependerá del propósito del análisis qué método se debe emplear.