Lente de Lüneburg

Lente de índice de gradiente simétrica esférica

Sección transversal de la lente de Luneburgo estándar, con sombreado azul proporcional al índice de refracción.

Una lente de Luneburg (originalmente en alemán Lüneburg -Linse ) es una lente de índice de gradiente esféricamente simétrica . El índice de refracción n de una lente de Luneburg típica disminuye radialmente desde el centro hacia la superficie exterior. Pueden fabricarse para su uso con radiación electromagnética, desde luz visible hasta ondas de radio .

Para determinados perfiles de índice, la lente formará imágenes geométricas perfectas de dos esferas concéntricas dadas una sobre otra. Hay un número infinito de perfiles de índice de refracción que pueden producir este efecto. La solución más simple de este tipo fue propuesta por Rudolf Luneburg en 1944. ^{[1] La solución de Luneburg para el índice de refracción crea dos} focos conjugados fuera de la lente. La solución adopta una forma simple y explícita si un punto focal se encuentra en el infinito y el otro en la superficie opuesta de la lente. J. Brown y AS Gutman propusieron posteriormente soluciones que generan un punto focal interno y un punto focal externo. ^{[2] [3]} Estas soluciones no son únicas; el conjunto de soluciones está definido por un conjunto de integrales definidas que deben evaluarse numéricamente. ^[4]

Diseños

La solución de Lüneburg

Una lente de Luneburg convierte una fuente puntual en un haz colimado cuando la fuente se coloca en su borde.

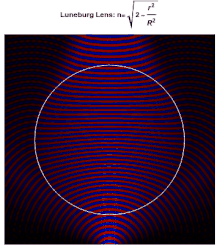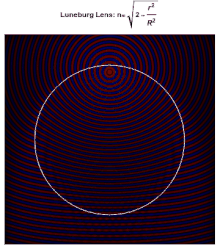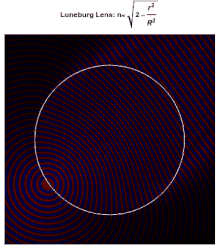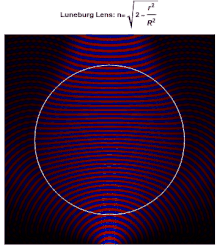
Cada punto de la superficie de una lente de Luneburg ideal es el punto focal de la radiación paralela que incide en el lado opuesto. Idealmente, la constante dieléctrica del material que compone la lente cae de 2 en su centro a 1 en su superficie (o equivalentemente, el índice de refracción cae de a 1), según ${\displaystyle \epsilon _{r}}$ ${\displaystyle n}$ ${\displaystyle {\sqrt {2}}}$

${\displaystyle n={\sqrt {\epsilon _{r}}}={\sqrt {2-\left({\frac {r}{R}}\right)^{2}}},}$

donde es el radio de la lente. Como el índice de refracción en la superficie es el mismo que el del medio circundante, no se produce reflexión en la superficie. Dentro de la lente, las trayectorias de los rayos son arcos de elipses . ${\displaystyle R}$

La lente ojo de pez de Maxwell

Sección transversal de la lente ojo de pez de Maxwell, con sombreado azul que representa el aumento del índice de refracción.

La lente ojo de pez de Maxwell es también un ejemplo de la lente de Luneburg generalizada. La lente ojo de pez, que Maxwell describió por completo por primera vez en 1854 ^[5] (y por lo tanto es anterior a la solución de Luneburg), tiene un índice de refracción que varía según

${\displaystyle n(r)={\sqrt {\epsilon _{r}}}={\frac {n_{0}}{1+\left({\frac {r}{R}}\right)^{2}}},}$

donde es el índice de refracción en el centro de la lente y es el radio de la superficie esférica de la lente. ^[6] El índice de refracción en la superficie de la lente es . La lente proyecta cada punto de la superficie esférica hacia el punto opuesto de la superficie. Dentro de la lente, las trayectorias de los rayos son arcos de círculos. ${\displaystyle n_{0}}$ ${\displaystyle R}$ ${\displaystyle n_{0}/2}$

Publicación y atribución

Las propiedades de esta lente se describen en uno de los numerosos problemas o acertijos que se presentaron en el Cambridge and Dublin Mathematical Journal de 1853. ^[7] El desafío consiste en encontrar el índice de refracción en función del radio, dado que un rayo describe una trayectoria circular, y además demostrar las propiedades de enfoque de la lente. La solución se da en la edición de 1854 de la misma revista. ^[5] Los problemas y las soluciones se publicaron originalmente de forma anónima, pero la solución de este problema (y de otro más) se incluyó en The Scientific Papers of James Clerk Maxwell de Niven , ^[8] que se publicó 11 años después de la muerte de Maxwell.

Aplicaciones

En la práctica, las lentes de Luneburg son normalmente estructuras en capas de capas concéntricas discretas, cada una de ellas con un índice de refracción diferente. Estas capas forman un perfil de índice de refracción escalonado que difiere ligeramente de la solución de Luneburg. Este tipo de lente se emplea normalmente para frecuencias de microondas , especialmente para construir antenas de microondas eficientes y patrones de calibración de radar . Los análogos cilíndricos de la lente de Luneburg también se utilizan para colimar la luz de los diodos láser .

Reflector de radar

Reflectores de Luneburg (la protuberancia marcada) en un F-35

Se puede fabricar un reflector de radar a partir de una lente de Luneburg metalizando partes de su superficie. La radiación de un transmisor de radar distante se enfoca en la parte inferior de la metalización en el lado opuesto de la lente; allí se refleja y se enfoca de nuevo hacia la estación de radar. Una dificultad con este esquema es que las regiones metalizadas bloquean la entrada o salida de la radiación en esa parte de la lente, pero las regiones no metalizadas dan lugar a un punto ciego en el lado opuesto.

Los reflectores de radar de tipo lente Luneburg removible se colocan a veces en los aviones militares para hacer visibles a los aviones furtivos durante las operaciones de entrenamiento o para ocultar su verdadera firma de radar. A diferencia de otros tipos de reflectores de radar, su forma no afecta el manejo del avión. ^{[9] [10]}

Antena de microondas

Radar 3D tipo 984 en el HMS  Victorious , 1961, utilizando una lente Luneburg

Una lente de Luneburg puede utilizarse como base de una antena de radio de alta ganancia. Esta antena es comparable a una antena parabólica , pero utiliza la lente en lugar de un reflector parabólico como elemento de enfoque principal. Al igual que con la antena parabólica, se coloca en el foco una alimentación hacia el receptor o desde el transmisor, que normalmente consiste en una antena de bocina . El centro de fase de la bocina de alimentación debe coincidir con el punto de enfoque, pero como el centro de fase está invariablemente algo dentro de la boca de la bocina, no se puede acercar directamente a la superficie de la lente. En consecuencia, es necesario utilizar una variedad de lente de Luneburg que enfoque algo más allá de su superficie, ^[11] en lugar de la lente clásica con el foco sobre la superficie.

Una antena con lente de Luneburg ofrece una serie de ventajas sobre una antena parabólica. Debido a que la lente es esféricamente simétrica, la antena se puede dirigir moviendo el alimentador alrededor de la lente, sin tener que girar toda la antena. Nuevamente, debido a que la lente es esféricamente simétrica, se puede utilizar una sola lente con varios alimentadores que miren en direcciones muy diferentes. Por el contrario, si se utilizan múltiples alimentadores con un reflector parabólico, todos deben estar dentro de un pequeño ángulo del eje óptico para evitar sufrir coma (una forma de desenfoque). Aparte de los sistemas desplazados , las antenas parabólicas sufren porque el alimentador y su estructura de soporte oscurecen parcialmente el elemento principal ( bloqueo de la apertura ); al igual que otros sistemas refractores, la antena con lente de Luneburg evita este problema.

Una variante de la antena de lente de Luneburg es la antena de lente de Luneburg hemisférica o antena reflectora de Luneburg . Esta utiliza solo un hemisferio de una lente de Luneburg, con la superficie cortada de la esfera apoyada sobre una placa de tierra metálica reflectante . La disposición reduce a la mitad el peso de la lente y la placa de tierra proporciona un medio de soporte conveniente. Sin embargo, la alimentación oscurece parcialmente la lente cuando el ángulo de incidencia sobre el reflector es menor a aproximadamente 45°.

Trayectoria de un rayo dentro de la lente

En cualquier lente esféricamente simétrica, cada rayo se encuentra íntegramente en un plano que pasa por el centro de la lente. La dirección inicial del rayo define una línea que, junto con el punto central de la lente, identifica un plano que la divide en dos. Al ser un plano de simetría de la lente, el gradiente del índice de refracción no tiene ningún componente perpendicular a este plano que haga que el rayo se desvíe hacia un lado o hacia el otro. En el plano, la simetría circular del sistema hace que sea conveniente utilizar coordenadas polares para describir la trayectoria del rayo. ${\displaystyle (r,\theta )}$

Dados dos puntos cualesquiera de un rayo (como el punto de entrada y el de salida de la lente), el principio de Fermat afirma que el camino que sigue el rayo entre ellos es el que puede recorrer en el menor tiempo posible. Dado que la velocidad de la luz en cualquier punto de la lente es inversamente proporcional al índice de refracción, y según Pitágoras , el tiempo de tránsito entre dos puntos y es ${\displaystyle (r_{1},\theta _{1})}$ ${\displaystyle (r_{2},\theta _{2})}$

${\displaystyle T=\int _{(r_{1},\theta _{1})}^{(r_{2},\theta _{2})}{\frac {n(r)}{c}}{\sqrt {(r\,d\theta )^{2}+dr^{2}}}={\frac {1}{c}}\int _{\theta _{1}}^{\theta _{2}}n(r){\sqrt {r^{2}+\left({\frac {dr}{d\theta }}\right)^{2}}}\,d\theta ,}$

donde es la velocidad de la luz en el vacío. Al minimizar esto se obtiene una ecuación diferencial de segundo orden que determina la dependencia de a lo largo de la trayectoria del rayo. Este tipo de problema de minimización se ha estudiado ampliamente en la mecánica de Lagrange y existe una solución preparada en forma de la identidad de Beltrami , que proporciona inmediatamente la primera integral de esta ecuación de segundo orden. Sustituyendo (donde representa ), en esta identidad se obtiene ${\displaystyle c}$ ${\displaystyle T}$ ${\displaystyle r}$ ${\displaystyle \theta }$ ${\displaystyle L(r,r')=n(r){\sqrt {r'^{2}+r^{2}}}}$ ${\displaystyle r'}$ ${\displaystyle {\tfrac {dr}{d\theta }}}$

${\displaystyle n(r){\sqrt {r'^{2}+r^{2}}}-n(r){\frac {r'^{2}}{\sqrt {r'^{2}+r^{2}}}}=h,}$

donde es una constante de integración . Esta ecuación diferencial de primer orden es separable , es decir, se puede reorganizar de modo que solo aparezca en un lado y solo en el otro: ^[1] ${\displaystyle h}$ ${\displaystyle r}$ ${\displaystyle \theta }$

${\displaystyle d\theta ={\frac {h}{r{\sqrt {{\big (}n(r){\big )}^{2}r^{2}-h^{2}}}}}\,dr.}$

El parámetro es una constante para cualquier rayo dado, pero difiere entre rayos que pasan a diferentes distancias del centro de la lente. Para rayos que pasan por el centro, es cero. En algunos casos especiales, como para el ojo de pez de Maxwell, esta ecuación de primer orden se puede integrar aún más para dar una fórmula para en función de . En general, proporciona las tasas relativas de cambio de y , que se pueden integrar numéricamente para seguir la trayectoria del rayo a través de la lente. ${\displaystyle h}$ ${\displaystyle \theta }$ ${\displaystyle r}$ ${\displaystyle \theta }$ ${\displaystyle r}$

Véase también

• Lente esférica
• Satélite BLITS (Ball Lens In The Space)
• Las lentes gravitacionales también tienen un índice de refracción que decrece radialmente.

Referencias

1. Luneburg, RK (1944). Teoría matemática de la óptica . Providence, Rhode Island: Universidad Brown. págs. 189–213.
2. Brown, J. (1953). Ingeniero inalámbrico . 30 : 250. {{cite journal}}: Falta o está vacío |title=( ayuda )
3. Gutman, AS (1954). "Lente de Luneberg modificada". J. Appl. Phys . 25 (7): 855–859. Código Bibliográfico :1954JAP....25..855G. doi :10.1063/1.1721757.
4. Morgan, SP (1958). "Solución general del problema de la lente de Luneburg". J. Appl. Phys . 29 (9): 1358–1368. Código Bibliográfico :1958JAP....29.1358M. doi :10.1063/1.1723441. S2CID  119949981.
5. "Soluciones de problemas (prob. 3, vol. VIII, pág. 188)". The Cambridge and Dublin Mathematical Journal . 9 . Macmillan: 9–11. 1854.
6. Badri, S Hadi y Gilarlue, MM (2019). "Lente ojo de pez de Maxwell como acoplador de potencia eficiente entre guías de onda de cristales fotónicos diferentes". Optik . 185 . Elsevier: 566–570. arXiv : 1904.01242 . Código Bibliográfico :2019Optik.185..566B. doi :10.1016/j.ijleo.2019.03.163. S2CID  91184610.{{cite journal}}: CS1 maint: varios nombres: lista de autores ( enlace )
7. "Problemas (3)". Revista matemática de Cambridge y Dublín . 8 . Macmillan: 188. 1853.
8. Niven, ed. (1890). Los documentos científicos de James Clerk Maxwell. Nueva York: Dover Publications. pág. 76.
9. "Mirando a través de una lente de Luneburg". www.eahison.com . 2019-08-08. Archivado desde el original el 2021-09-27 . Consultado el 2021-04-05 .
10. Lockie, Alex (5 de mayo de 2017). «Esta extraña modificación del F-35 acaba con su capacidad de sigilo cerca de las defensas rusas, y hay una buena razón para ello». Business Insider . Archivado desde el original el 25 de diciembre de 2023.
11. Lo, YT ; Lee, SW (1993). Manual de antenas: teoría de antenas. Springer. pág. 40. ISBN 9780442015930.

Enlaces externos

• Animación de propagación a través de una lente de Luneburg (antena dieléctrica) de YouTube
• Animación de una lente ojo de pez de Maxwell de YouTube
• Animación de la mitad de una lente ojo de pez de Maxwell (antena dieléctrica) de YouTube