La multiplicación reticular , también conocida como método italiano , método chino , reticular chino , multiplicación gelosia , [1] multiplicación por tamiz , shabakh , multiplicación diagonal o cuadrados venecianos , es un método de multiplicación que utiliza una red para multiplicar dos números de varios dígitos. Es matemáticamente idéntico al algoritmo de multiplicación larga más comúnmente utilizado , pero divide el proceso en pasos más pequeños, que algunos profesionales encuentran más fáciles de usar. [2]
El método ya había surgido en la época medieval y se ha utilizado durante siglos en muchas culturas diferentes. Todavía se enseña en ciertos programas de estudios en la actualidad. [3] [4]
Se dibuja una cuadrícula y cada celda se divide en diagonal. Los dos multiplicandos del producto que se va a calcular se escriben en la parte superior y derecha de la cuadrícula, respectivamente, con un dígito por columna en la parte superior para el primer multiplicando (el número escrito de izquierda a derecha) y un dígito por fila en la parte inferior derecha para el segundo multiplicando (el número escrito de arriba hacia abajo). Luego, cada celda de la cuadrícula se llena con el producto de su dígito de columna y fila.
Como ejemplo, considere la multiplicación de 58 por 213. Después de escribir los multiplicandos en los lados, considere cada celda, comenzando con la celda superior izquierda. En este caso, el dígito de la columna es 5 y el dígito de la fila es 2. Escriba su producto, 10, en la celda, con el dígito 1 sobre la diagonal y el dígito 0 debajo de la diagonal (vea la imagen del Paso 1).
Si al producto simple le falta un dígito en el lugar de las decenas, simplemente rellene el lugar de las decenas con un 0. [2]
_multiplication_algorithm.svg/1280px-Example_of_step_1_of_lattice_(shabakh)_multiplication_algorithm.svg.png)
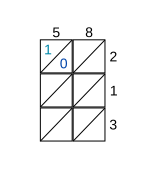
Una vez que todas las celdas se han llenado de esta manera, se suman los dígitos de cada diagonal, comenzando por la diagonal inferior derecha y terminando por la diagonal superior izquierda. Cada suma diagonal se escribe donde termina la diagonal. Si la suma contiene más de un dígito, el valor de la posición de las decenas se traslada a la siguiente diagonal (ver Paso 2).
_multiplication_algorithm.svg/1280px-Example_of_step_2_of_lattice_(shabakh)_multiplication_algorithm.svg.png)
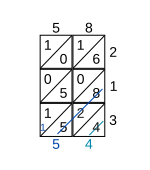
Los números se rellenan a la izquierda y a la parte inferior de la cuadrícula, y la respuesta son los números leídos hacia abajo (a la izquierda) y a lo ancho (abajo). En el ejemplo que se muestra, el resultado de la multiplicación de 58 por 213 es 12354.
_multiplication_algorithm.svg/1280px-Example_of_step_3_of_lattice_(shabakh)_multiplication_algorithm.svg.png)
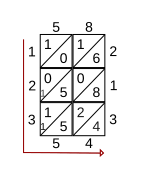
La técnica de la red también se puede utilizar para multiplicar fracciones decimales . Por ejemplo, para multiplicar 5,8 por 2,13, el proceso es el mismo que para multiplicar 58 por 213, como se describe en la sección anterior. Para encontrar la posición del punto decimal en la respuesta final, se puede dibujar una línea vertical desde el punto decimal en 5,8 y una línea horizontal desde el punto decimal en 2,13. (Vea la imagen del Paso 4). La diagonal de la cuadrícula a través de la intersección de estas dos líneas determina entonces la posición del punto decimal en el resultado. [2] En el ejemplo que se muestra, el resultado de la multiplicación de 5,8 y 2,13 es 12,354.
_multiplication_algorithm.svg/1280px-Example_of_step_4_of_lattice_(shabakh)_multiplication_algorithm.svg.png)
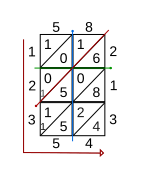
Aunque la multiplicación reticular se ha utilizado históricamente en muchas culturas, en el comentario sobre el libro de matemáticas indias del siglo XII 'Lilavati' de Bhaskaracharya se menciona un método llamado 'Kapat-sandhi', muy similar al método reticular. Se está investigando dónde surgió por primera vez y si se desarrolló de forma independiente en más de una región del mundo. [5] El primer uso registrado de la multiplicación reticular: [6]
El matemático y educador David Eugene Smith afirmó que la multiplicación reticular llegó a Italia desde Oriente Medio. [7] Esto se refuerza al observar que el término árabe para el método, shabakh , tiene el mismo significado que el término italiano para el método, gelosia , es decir, la reja o rejilla metálica (celosía) para una ventana.
A veces se afirma erróneamente que la multiplicación reticular fue descrita por Muḥammad ibn Mūsā al-Khwārizmī (Bagdad, c. 825) o por Fibonacci en su Liber Abaci (Italia, 1202, 1228). [8] De hecho, sin embargo, no se ha encontrado ningún uso de la multiplicación reticular por ninguno de estos dos autores. En el Capítulo 3 de su Liber Abaci , Fibonacci describe una técnica relacionada de multiplicación mediante lo que denominó quadrilatero in forma scacherii ("rectángulo en forma de tablero de ajedrez"). En esta técnica, las celdas cuadradas no se subdividen en diagonal; solo se escribe el dígito de orden más bajo en cada celda, mientras que cualquier dígito de orden superior debe recordarse o registrarse en otro lugar y luego "llevarse" para agregarse a la siguiente celda. Esto contrasta con la multiplicación en red, una característica distintiva de la cual es que cada celda del rectángulo tiene su propio lugar correcto para el dígito de acarreo; esto también implica que las celdas se pueden llenar en cualquier orden deseado. Swetz [9] compara y contrasta la multiplicación por gelosia (red), por scacherii (tablero de ajedrez) y otros métodos de tabla.
Otros usos históricos notables de la multiplicación reticular incluyen: [6]
Derivaciones de este método también aparecieron en las obras del siglo XVI Umdet-ul Hisab del polímata otomano-bosnio Matrakçı Nasuh . [10] La versión triangular de Matrakçı Nasuh de la técnica de multiplicación se ve en el ejemplo que muestra 155 x 525 a la derecha, y se explica en el ejemplo que muestra 236 x 175 en la figura de la izquierda. [11]
El mismo principio descrito por Matrakçı Nasuh sirvió de base para el desarrollo posterior de las varas de cálculo conocidas como huesos de Napier (Escocia, 1617) y reglas de Genaille-Lucas (Francia, finales del siglo XIX).