Teoría del aprendizaje estadístico

Marco para el aprendizaje automático

La teoría del aprendizaje estadístico es un marco para el aprendizaje automático que se basa en los campos de la estadística y el análisis funcional . ^{[1] [2] [3]} La teoría del aprendizaje estadístico se ocupa del problema de inferencia estadística de encontrar una función predictiva basada en datos. La teoría del aprendizaje estadístico ha dado lugar a aplicaciones exitosas en campos como la visión por computadora , el reconocimiento de voz y la bioinformática .

Introducción

Los objetivos del aprendizaje son la comprensión y la predicción. El aprendizaje se divide en muchas categorías, incluido el aprendizaje supervisado , el aprendizaje no supervisado , el aprendizaje en línea y el aprendizaje por refuerzo . Desde la perspectiva de la teoría estadística del aprendizaje, el aprendizaje supervisado se comprende mejor. ^[4] El aprendizaje supervisado implica aprender a partir de un conjunto de datos de entrenamiento . Cada punto del entrenamiento es un par entrada-salida, donde la entrada se asigna a una salida. El problema de aprendizaje consiste en inferir la función que se mapea entre la entrada y la salida, de modo que la función aprendida pueda usarse para predecir la salida a partir de entradas futuras.

Dependiendo del tipo de resultado, los problemas de aprendizaje supervisado son problemas de regresión o problemas de clasificación . Si la salida toma un rango continuo de valores, es un problema de regresión. Usando la ley de Ohm como ejemplo, se podría realizar una regresión con voltaje como entrada y corriente como salida. La regresión encontraría que la relación funcional entre voltaje y corriente es , tal que ${\displaystyle R}$

${\displaystyle V=IR}$

Los problemas de clasificación son aquellos en los que la salida será un elemento de un conjunto discreto de etiquetas. La clasificación es muy común para las aplicaciones de aprendizaje automático. En el reconocimiento facial , por ejemplo, una imagen del rostro de una persona sería la entrada y la etiqueta de salida sería el nombre de esa persona. La entrada estaría representada por un gran vector multidimensional cuyos elementos representan píxeles en la imagen.

Después de aprender una función basada en los datos del conjunto de entrenamiento, esa función se valida en un conjunto de datos de prueba, datos que no aparecieron en el conjunto de entrenamiento.

Descripción formal

Considere el espacio vectorial de todas las entradas posibles y el espacio vectorial de todas las salidas posibles. La teoría del aprendizaje estadístico adopta la perspectiva de que existe alguna distribución de probabilidad desconocida en el espacio del producto , es decir, existe alguna incógnita . El conjunto de entrenamiento se compone de muestras de esta distribución de probabilidad y se anota ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle Z=X\times Y}$ ${\displaystyle p(z)=p({\vec {x}},y)}$ ${\displaystyle n}$

${\displaystyle S=\{({\vec {x}}_{1},y_{1}),\dots ,({\vec {x}}_{n},y_{n})\}=\{{\vec {z}}_{1},\dots ,{\vec {z}}_{n}\}}$

Cada es un vector de entrada de los datos de entrenamiento y es la salida que le corresponde. ${\displaystyle {\vec {x}}_{i}}$ ${\displaystyle y_{i}}$

En este formalismo, el problema de inferencia consiste en encontrar una función tal que . Sea un espacio de funciones llamado espacio de hipótesis. El espacio de hipótesis es el espacio de funciones en el que buscará el algoritmo. Sea la función de pérdida , una métrica para la diferencia entre el valor previsto y el valor real . El riesgo esperado se define como ${\displaystyle f:X\to Y}$ ${\displaystyle f({\vec {x}})\sim y}$ ${\displaystyle {\mathcal {H}}}$ ${\displaystyle f:X\to Y}$ ${\displaystyle V(f({\vec {x}}),y)}$ ${\displaystyle f({\vec {x}})}$ ${\displaystyle y}$

${\displaystyle I[f]=\displaystyle \int _{X\times Y}V(f({\vec {x}}),y)\,p({\vec {x}},y)\,d{\vec {x}}\,dy}$

La función objetivo, la mejor función posible que se puede elegir, está dada por la que satisface ${\displaystyle f}$ ${\displaystyle f}$

${\displaystyle f=\mathrm {argmin} _{\{h\in {\mathcal {H}}\}}I[h]}$

Como se desconoce la distribución de probabilidad , se debe utilizar una medida aproximada del riesgo esperado. Esta medida se basa en el conjunto de entrenamiento, una muestra de esta distribución de probabilidad desconocida. Se llama riesgo empírico. ${\displaystyle p({\vec {x}},y)}$

${\displaystyle I_{S}[f]={\frac {1}{n}}\displaystyle \sum _{i=1}^{n}V(f({\vec {x}}_{i}),y_{i})}$

Un algoritmo de aprendizaje que elige la función que minimiza el riesgo empírico se llama minimización del riesgo empírico . ${\displaystyle f_{S}}$

Funciones de pérdida

La elección de la función de pérdida es un factor determinante sobre la función que será elegida por el algoritmo de aprendizaje. La función de pérdida también afecta la tasa de convergencia de un algoritmo. Es importante que la función de pérdida sea convexa . ^[5] ${\displaystyle f_{S}}$

Se utilizan diferentes funciones de pérdida dependiendo de si el problema es de regresión o de clasificación.

Regresión

La función de pérdida más común para la regresión es la función de pérdida cuadrada (también conocida como norma L2 ). Esta conocida función de pérdida se utiliza en la regresión de mínimos cuadrados ordinarios . La forma es:

${\displaystyle V(f({\vec {x}}),y)=(y-f({\vec {x}}))^{2}}$

La pérdida de valor absoluto (también conocida como norma L1 ) también se utiliza a veces:

${\displaystyle V(f({\vec {x}}),y)=|y-f({\vec {x}})|}$

Clasificación

En cierto sentido, la función indicadora 0-1 es la función de pérdida más natural para la clasificación. Toma el valor 0 si la salida prevista es la misma que la salida real, y toma el valor 1 si la salida prevista es diferente de la salida real. Para la clasificación binaria con , esto es: ${\displaystyle Y=\{-1,1\}}$

${\displaystyle V(f({\vec {x}}),y)=\theta (-yf({\vec {x}}))}$

¿ Dónde está la función de paso de Heaviside ? ${\displaystyle \theta }$

Regularización

Esta imagen representa un ejemplo de sobreajuste en el aprendizaje automático. Los puntos rojos representan datos del conjunto de entrenamiento. La línea verde representa la verdadera relación funcional, mientras que la línea azul muestra la función aprendida, que se ha sobreajustado a los datos del conjunto de entrenamiento.

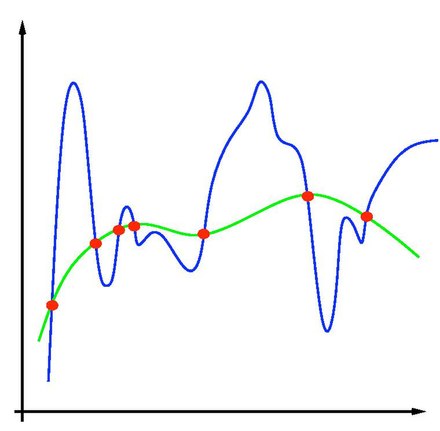
En los problemas de aprendizaje automático, un problema importante que surge es el del sobreajuste . Debido a que el aprendizaje es un problema de predicción, el objetivo no es encontrar una función que se ajuste mejor a los datos (observados previamente), sino encontrar una que prediga con mayor precisión la salida de entradas futuras. La minimización empírica del riesgo corre el riesgo de sobreajuste: encontrar una función que coincida exactamente con los datos pero que no prediga bien la producción futura.

El sobreajuste es sintomático de soluciones inestables; una pequeña perturbación en los datos del conjunto de entrenamiento provocaría una gran variación en la función aprendida. Se puede demostrar que si se puede garantizar la estabilidad de la solución, también se garantizan la generalización y la coherencia. ^{[6] [7]} La ​​regularización puede resolver el problema de sobreajuste y darle estabilidad.

La regularización se puede lograr restringiendo el espacio de hipótesis . Un ejemplo común sería restringir a funciones lineales: esto puede verse como una reducción al problema estándar de regresión lineal . También podría restringirse a polinomios de grado , exponenciales o funciones acotadas en L1 . La restricción del espacio de hipótesis evita el sobreajuste porque la forma de las funciones potenciales es limitada y, por lo tanto, no permite la elección de una función que proporcione un riesgo empírico arbitrariamente cercano a cero. ${\displaystyle {\mathcal {H}}}$ ${\displaystyle {\mathcal {H}}}$ ${\displaystyle {\mathcal {H}}}$ ${\displaystyle p}$

Un ejemplo de regularización es la regularización de Tikhonov . Consiste en minimizar

${\displaystyle {\frac {1}{n}}\displaystyle \sum _{i=1}^{n}V(f({\vec {x}}_{i}),y_{i})+\gamma \|f\|_{\mathcal {H}}^{2}}$

donde es un parámetro fijo y positivo, el parámetro de regularización. La regularización de Tikhonov garantiza la existencia, unicidad y estabilidad de la solución. ^[8] ${\displaystyle \gamma }$

Ver también

• La reproducción de espacios de Hilbert del núcleo es una opción útil para . ${\displaystyle {\mathcal {H}}}$
• Métodos de gradiente proximal para el aprendizaje.
• Complejidad de Rademacher
• Dimensión Vapnik-Chervonenkis

Referencias

1. Vladimir Vapnik (1995) La naturaleza de la teoría del aprendizaje estadístico , Springer Nueva York ISBN  978-1-475-72440-0 .
2. Trevor Hastie , Robert Tibshirani, Jerome Friedman (2009) Los elementos del aprendizaje estadístico , Springer-Verlag ISBN 978-0-387-84857-0 . 
3. Mohri, Mehryar ; Rostamizadeh, Afshin; Talwalkar, Ameet (2012). Fundamentos del aprendizaje automático . Estados Unidos, Massachusetts: MIT Press. ISBN 9780262018258.
4. Tomaso Poggio, Lorenzo Rosasco y otros. Teoría y aplicaciones del aprendizaje estadístico , 2012, Clase 1
5. Rosasco, L., De Vito, E., Caponnetto, A., Piana, M. y Verri A. 2004. Computación neuronal Vol. 16, págs. 1063-1076
6. Vapnik, VN y Chervonenkis, AY 1971. Sobre la convergencia uniforme de frecuencias relativas de eventos con sus probabilidades. Teoría de la probabilidad y sus aplicaciones Vol. 16, págs. 264-280.
7. Mukherjee, S., Niyogi, P. Poggio, T. y Rifkin, R. 2006. Teoría del aprendizaje: la estabilidad es suficiente para la generalización y necesaria y suficiente para la coherencia de la minimización del riesgo empírico. Avances en Matemática Computacional . Vol. 25, págs. 161-193.
8. Tomaso Poggio, Lorenzo Rosasco y otros. Teoría y aplicaciones del aprendizaje estadístico , 2012, clase 2