La variación de la presión vertical es la variación de la presión en función de la altura . Dependiendo del fluido en cuestión y del contexto al que se hace referencia, también puede variar significativamente en dimensiones perpendiculares a la altura, y estas variaciones tienen relevancia en el contexto de la fuerza del gradiente de presión y sus efectos. Sin embargo, la variación vertical es especialmente significativa, ya que resulta de la atracción de la gravedad sobre el fluido; es decir, para el mismo fluido dado, una disminución en la altura dentro de él corresponde a una columna más alta de fluido que pesa sobre ese punto.
Una versión relativamente simple [1] de la variación de la presión vertical del fluido es simplemente que la diferencia de presión entre dos elevaciones es el producto del cambio de elevación, la gravedad y la densidad . La ecuación es la siguiente: donde
El símbolo delta indica un cambio en una variable dada. Como g es negativo, un aumento de altura corresponderá a una disminución de la presión, lo que encaja con el razonamiento mencionado anteriormente sobre el peso de una columna de fluido.
Cuando la densidad y la gravedad son aproximadamente constantes (es decir, para cambios relativamente pequeños en la altura), simplemente multiplicando la diferencia de altura, la gravedad y la densidad se obtendrá una buena aproximación de la diferencia de presión. Si se sabe que la presión en un punto de un líquido con densidad uniforme ρ es P 0 , entonces la presión en otro punto es P 1 :
donde h 1 - h 0 es la distancia vertical entre los dos puntos. [2]
Cuando se superponen distintos fluidos, la diferencia de presión total se obtendrá sumando las dos diferencias de presión; la primera es desde el punto 1 hasta el límite, la segunda es desde el límite hasta el punto 2; lo que implicaría simplemente sustituir los valores de ρ y Δ h para cada fluido y obtener la suma de los resultados. Si la densidad del fluido varía con la altura, se requerirá una integración matemática.
El que la densidad y la gravedad puedan o no aproximarse razonablemente como constantes depende del nivel de precisión necesario, pero también de la escala de longitud de la diferencia de altura, ya que la gravedad y la densidad también disminuyen con una mayor elevación. Para la densidad en particular, el fluido en cuestión también es relevante; el agua de mar , por ejemplo, se considera un fluido incompresible ; su densidad puede variar con la altura, pero de manera mucho menos significativa que la del aire. Por lo tanto, la densidad del agua puede aproximarse más razonablemente como constante que la del aire y, dada la misma diferencia de altura, las diferencias de presión en el agua son aproximadamente iguales a cualquier altura.
La fórmula barométrica depende únicamente de la altura de la cámara de fluido, y no de su anchura o longitud. Dada una altura lo suficientemente grande, se puede alcanzar cualquier presión. Esta característica de la hidrostática se ha denominado paradoja hidrostática . Como lo expresó WH Besant , [3]
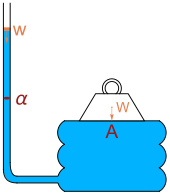
El científico flamenco Simon Stevin fue el primero en explicar matemáticamente la paradoja. [4] En 1916, Richard Glazebrook mencionó la paradoja hidrostática al describir un sistema que atribuyó a Pascal : un peso pesado W reposa sobre una tabla con un área A que descansa sobre una vejiga de fluido conectada a un tubo vertical con un área de sección transversal α. Al verter agua de peso w por el tubo, eventualmente se elevará el peso pesado. El equilibrio de fuerzas conduce a la ecuación
Glazebrook dice: "Si se hace que el área de la placa sea considerable y la del tubo pequeña, un peso grande W puede ser soportado por un peso pequeño w de agua. Este hecho a veces se describe como la paradoja hidrostática". [5]
La maquinaria hidráulica utiliza este fenómeno para multiplicar la fuerza o el par. Para enseñar este fenómeno se utilizan demostraciones de la paradoja hidrostática. [6] [7]
Si se analiza la variación de la presión vertical de la atmósfera de la Tierra , la escala de longitud es muy significativa ( la troposfera por sí sola tiene varios kilómetros de altura; la termosfera varios cientos de kilómetros) y el fluido involucrado (aire) es compresible. La gravedad todavía puede aproximarse razonablemente como constante, porque las escalas de longitud del orden de kilómetros son todavía pequeñas en comparación con el radio de la Tierra, que es en promedio de unos 6371 km, [8] y la gravedad es una función de la distancia desde el núcleo de la Tierra. [9]
La densidad, por otra parte, varía más significativamente con la altura. De la ley de los gases ideales se desprende que donde
En términos más simples, la densidad del aire depende de la presión del aire. Dado que la presión del aire también depende de la densidad del aire, sería fácil tener la impresión de que se trata de una definición circular , pero es simplemente la interdependencia de diferentes variables. Esto produce una fórmula más precisa, de la forma donde
Por lo tanto, en lugar de que la presión sea una función lineal de la altura, como se podría esperar de la fórmula más simple dada en la sección "fórmula básica", se representa con mayor precisión como una función exponencial de la altura.
Obsérvese que en esta simplificación, la temperatura se considera constante, aunque también varía con la altura. Sin embargo, la variación de temperatura en las capas inferiores de la atmósfera ( troposfera , estratosfera ) es de tan solo unas decenas de grados, a diferencia de su temperatura termodinámica , que es de cientos, por lo que la variación de temperatura es razonablemente pequeña y, por lo tanto, se ignora. Para diferencias de altura más pequeñas, incluidas las de arriba a abajo incluso de los edificios más altos (como la Torre CN ) o para montañas de tamaño comparable, la variación de temperatura estará fácilmente dentro de los dígitos de un solo dígito. (Véase también gradiente térmico ).
Se utiliza una derivación alternativa, mostrada por la Portland State Aerospace Society [10] , para dar la altura como una función de la presión. Esto puede parecer contra-intuitivo, ya que la presión resulta de la altura y no al revés, pero una fórmula de este tipo puede ser útil para encontrar la altura en función de la diferencia de presión cuando se conoce la última y no la primera. Se presentan diferentes fórmulas para diferentes tipos de aproximaciones; para comparar con la fórmula anterior, la primera a la que se haga referencia en el artículo será la que aplique la misma aproximación de temperatura constante; en cuyo caso: donde (con los valores utilizados en el artículo)
Una fórmula más general derivada del mismo artículo da cuenta de un cambio lineal de la temperatura en función de la altura (índice de caída), y se reduce a lo anterior cuando la temperatura es constante: donde
y las demás cantidades son las mismas que las anteriores. Esta es la fórmula recomendada para utilizar.
Stevin proporciona una demostración matemática original de la llamada paradoja hidrostática.
![]() Medios relacionados con Paradoja hidrostática en Wikimedia Commons
Medios relacionados con Paradoja hidrostática en Wikimedia Commons