Lazo (estadísticas)

Método estadístico

En estadística y aprendizaje automático , lazo ( operador de selección y contracción mínima absoluta ; también lazo o LASSO ) es un método de análisis de regresión que realiza tanto la selección de variables como la regularización para mejorar la precisión de la predicción y la interpretabilidad del modelo estadístico resultante . El método del lazo supone que los coeficientes del modelo lineal son escasos, lo que significa que pocos de ellos son distintos de cero. Fue introducido originalmente en la geofísica , ^[1] y posteriormente por Robert Tibshirani , ^[2] quien acuñó el término.

Lasso se formuló originalmente para modelos de regresión lineal . Este simple caso revela mucho sobre el estimador. Estos incluyen su relación con la regresión de crestas y la mejor selección de subconjuntos y las conexiones entre las estimaciones del coeficiente de lazo y el llamado umbral suave. También revela que (al igual que la regresión lineal estándar) las estimaciones de los coeficientes no necesitan ser únicas si las covariables son colineales .

Aunque originalmente se definió para la regresión lineal, la regularización de lazo se extiende fácilmente a otros modelos estadísticos, incluidos los modelos lineales generalizados , las ecuaciones de estimación generalizadas , los modelos de riesgos proporcionales y los estimadores M. ^{[2] [3]} La capacidad de Lasso para realizar la selección de subconjuntos depende de la forma de la restricción y tiene una variedad de interpretaciones, incluso en términos de geometría , estadística bayesiana y análisis convexo .

El LASSO está estrechamente relacionado con la eliminación de ruido de búsqueda de bases .

Historia

Lasso se introdujo para mejorar la precisión de la predicción y la interpretabilidad de los modelos de regresión. Selecciona un conjunto reducido de covariables conocidas para su uso en un modelo. ^{[2] [1]}

Lasso se desarrolló de forma independiente en la literatura de geofísica en 1986, basándose en trabajos anteriores que utilizaban la penalización tanto para el ajuste como para la penalización de los coeficientes. El estadístico Robert Tibshirani lo redescubrió y popularizó de forma independiente en 1996, basándose en el garrote no negativo de Breiman . ^{[1] [4]} ${\displaystyle \ell ^{1}}$

Antes de Lasso, el método más utilizado para elegir covariables era la selección por pasos . Ese enfoque solo mejora la precisión de la predicción en ciertos casos, como cuando solo unas pocas covariables tienen una fuerte relación con el resultado. Sin embargo, en otros casos, puede aumentar el error de predicción.

En ese momento, la regresión de crestas era la técnica más popular para mejorar la precisión de la predicción. La regresión de cresta mejora el error de predicción al reducir la suma de los cuadrados de los coeficientes de regresión a menos de un valor fijo para reducir el sobreajuste , pero no realiza la selección de covariables y, por lo tanto, no ayuda a que el modelo sea más interpretable.

Lasso logra ambos objetivos al forzar que la suma del valor absoluto de los coeficientes de regresión sea menor que un valor fijo, lo que obliga a ciertos coeficientes a cero, excluyéndolos del impacto en la predicción. Esta idea es similar a la regresión de crestas, que también reduce el tamaño de los coeficientes; sin embargo, la regresión de crestas no establece los coeficientes en cero (y, por lo tanto, no realiza la selección de variables ).

Forma básica

mínimos cuadrados

Considere una muestra que consta de N casos, cada uno de los cuales consta de p covariables y un único resultado. Sea el resultado y el vector covariable para el i- ^ésimo caso. Entonces el objetivo del lazo es resolver ${\displaystyle y_{i}}$ ${\displaystyle x_{i}:=(x_{1},x_{2},\ldots ,x_{p})_{i}^{T}}$

${\displaystyle \min _{\beta _{0},\beta }{\biggl \{}\sum _{i=1}^{N}{\bigl (}y_{i}-\beta _{0}-x_{i}^{T}\beta {\bigr )}^{2}{\biggr \}}{\text{ subject to }}\sum _{j=1}^{p}|\beta _{j}|\leq t.}$^[2]

Aquí está el coeficiente constante, es el vector de coeficientes y es un parámetro libre preespecificado que determina el grado de regularización. ${\displaystyle \beta _{0}}$ ${\displaystyle \beta :=(\beta _{1},\beta _{2},\ldots ,\beta _{p})}$ ${\displaystyle t}$

Sea la matriz de covariables, de modo que ^y sea la iésima fila de , la expresión se puede escribir de forma más compacta como ${\displaystyle X}$ ${\displaystyle X_{ij}=(x_{i})_{j}}$ ${\displaystyle x_{i}^{T}}$ ${\displaystyle X}$

${\displaystyle \min _{\beta _{0},\beta }\left\{\left\|y-\beta _{0}-X\beta \right\|_{2}^{2}\right\}{\text{ subject to }}\|\beta \|_{1}\leq t,}$

¿ Dónde está la norma estándar ? ${\displaystyle \|u\|_{p}={\biggl (}\sum _{i=1}^{N}|u_{i}|^{p}{\biggr )}^{1/p}}$ ${\displaystyle \ell ^{p}}$

Denotando la media escalar de los puntos de datos por y la media de las variables de respuesta por , la estimación resultante para es , de modo que ${\displaystyle x_{i}}$ ${\displaystyle {\bar {x}}}$ ${\displaystyle y_{i}}$ ${\displaystyle {\bar {y}}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle {\hat {\beta }}_{0}={\bar {y}}-{\bar {x}}^{T}\beta }$

${\displaystyle y_{i}-{\hat {\beta }}_{0}-x_{i}^{T}\beta =y_{i}-({\bar {y}}-{\bar {x}}^{T}\beta )-x_{i}^{T}\beta =(y_{i}-{\bar {y}})-(x_{i}-{\bar {x}})^{T}\beta ,}$

y por lo tanto es estándar trabajar con variables a las que se les ha hecho media cero. Además, las covariables suelen estar estandarizadas para que la solución no dependa de la escala de medición. ${\textstyle {\bigl (}\sum _{i=1}^{N}x_{i}^{2}=1{\bigr )}}$

Puede resultar útil reescribir

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\|y-X\beta \right\|_{2}^{2}\right\}{\text{ subject to }}\|\beta \|_{1}\leq t.}$

en la llamada forma lagrangiana

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\|y-X\beta \right\|_{2}^{2}+\lambda \|\beta \|_{1}\right\}}$

donde la relación exacta entre y depende de los datos. ${\displaystyle t}$ ${\displaystyle \lambda }$

Covariables ortonormales

Ahora se pueden considerar algunas propiedades básicas del estimador de lazo.

Suponiendo primero que las covariables son ortonormales de modo que , donde está el delta de Kronecker , o, equivalentemente, , luego usando métodos subgradientes se puede demostrar que ${\displaystyle x_{i}^{T}x_{j}=\delta _{ij}}$ ${\displaystyle \delta _{ij}}$ ${\displaystyle X^{T}X=I}$

${\displaystyle {\begin{aligned}{\hat {\beta }}_{j}={}&S_{N\lambda }({\hat {\beta }}{}_{j}^{\!\;{\text{OLS}}})={\hat {\beta }}{}_{j}^{\!\;{\text{OLS}}}\max {\Biggl (}0,1-{\frac {N\lambda }{{\bigl |}{\hat {\beta }}{}_{j}^{\!\;{\text{OLS}}}{\bigr |}}}{\Biggr )}\\&{\text{ where }}{\hat {\beta }}{}_{j}^{\!\;{\text{OLS}}}=(X^{T}X)^{-1}X^{T}y=X^{T}y\end{aligned}}}$ ^[2]

${\displaystyle S_{\alpha }}$se conoce como operador de umbral suave , ya que traduce los valores hacia cero (haciéndolos exactamente cero si son lo suficientemente pequeños) en lugar de establecer valores más pequeños en cero y dejar los más grandes intactos como lo haría el operador de umbral estricto , a menudo denominado . ${\displaystyle H_{\alpha }}$

En la regresión de crestas el objetivo es minimizar

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\|y-X\beta \|_{2}^{2}+\lambda \|\beta \|_{2}^{2}\right\}}$

Usando y la fórmula de regresión de crestas: , ^[5] se obtiene: ${\displaystyle X^{T}X=I}$ ${\displaystyle {\hat {\beta }}=\left((X^{T}X)+N\lambda I\right)^{-1}X^{T}y}$

${\displaystyle {\hat {\beta }}_{j}=(1+N\lambda )^{-1}{\hat {\beta }}{}_{j}^{\!\;{\text{OLS}}}.}$

La regresión de cresta reduce todos los coeficientes en un factor uniforme de y no establece ningún coeficiente en cero. ^[6] ${\displaystyle (1+N\lambda )^{-1}}$

También se puede comparar con la regresión con la mejor selección de subconjuntos , en la que el objetivo es minimizar

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\|y-X\beta \right\|_{2}^{2}+\lambda \|\beta \|_{0}\right\}}$

¿Dónde está la " norma", que se define como si exactamente m componentes de z fueran distintos de cero? En este caso se puede demostrar que ${\displaystyle \|\cdot \|_{0}}$ ${\displaystyle \ell ^{0}}$ ${\displaystyle \|z\|=m}$

${\displaystyle {\hat {\beta }}_{j}=H_{\sqrt {N\lambda }}\left({\hat {\beta }}{}_{j}^{\!\;{\text{OLS}}}\right)={\hat {\beta }}{}_{j}^{\!\;{\text{OLS}}}\mathrm {I} \left({\bigl |}{\hat {\beta }}{}_{j}^{\!\;{\text{OLS}}}{\bigr |}\geq {\sqrt {N\lambda }}\right)}$

donde está la llamada función de umbral estricto y es una función indicadora (es 1 si su argumento es verdadero y 0 en caso contrario). ${\displaystyle H_{\alpha }}$ ${\displaystyle \mathrm {I} }$

Por lo tanto, las estimaciones del lazo comparten características de la regresión de selección de cresta y del mejor subconjunto, ya que ambas reducen la magnitud de todos los coeficientes, como la regresión de cresta, y establecen algunos de ellos en cero, como en el caso de selección del mejor subconjunto. Además, mientras que la regresión de cresta escala todos los coeficientes mediante un factor constante, el lazo traduce los coeficientes hacia cero mediante un valor constante y los establece en cero si lo alcanzan.

Covariables correlacionadas

En un caso especial, dos covariables, digamos j y k , son idénticas para cada observación, de modo que , donde . Entonces los valores de y que minimizan la función objetivo del lazo no están determinados de forma única. De hecho, si algunos en los cuales , entonces si se reemplaza por y por , mientras se mantienen todos los demás fijos, se obtiene una nueva solución, entonces la función objetivo del lazo tiene un continuo de minimizadores válidos. ^[7] Se han diseñado varias variantes del lazo, incluida la regularización de red elástica , para abordar esta deficiencia. ${\displaystyle x_{(j)}=x_{(k)}}$ ${\displaystyle x_{(j),i}=x_{(k),i}}$ ${\displaystyle \beta _{j}}$ ${\displaystyle \beta _{k}}$ ${\displaystyle {\hat {\beta }}}$ ${\displaystyle {\hat {\beta }}_{j}{\hat {\beta }}_{k}\geq 0}$ ${\displaystyle s\in [0,1]}$ ${\displaystyle {\hat {\beta }}_{j}}$ ${\displaystyle s({\hat {\beta }}_{j}+{\hat {\beta }}_{k})}$ ${\displaystyle {\hat {\beta }}_{k}}$ ${\displaystyle (1-s)({\hat {\beta }}_{j}+{\hat {\beta }}_{k})}$ ${\displaystyle {\hat {\beta }}_{i}}$

forma general

La regularización de lazo se puede extender a otras funciones objetivas , como las de modelos lineales generalizados , ecuaciones de estimación generalizadas , modelos de riesgos proporcionales y estimadores M. ^{[2] [3]} Dada la función objetivo

${\displaystyle {\frac {1}{N}}\sum _{i=1}^{N}f(x_{i},y_{i},\alpha ,\beta )}$

La versión regularizada con lazo del estimador es la solución a

${\displaystyle \min _{\alpha ,\beta }{\frac {1}{N}}\sum _{i=1}^{N}f(x_{i},y_{i},\alpha ,\beta ){\text{ subject to }}\|\beta \|_{1}\leq t}$

donde solo se penaliza mientras que es libre de tomar cualquier valor permitido, al igual que no se penalizó en el caso básico. ${\displaystyle \beta }$ ${\displaystyle \alpha }$ ${\displaystyle \beta _{0}}$

Interpretaciones

Interpretación geométrica

Formas de las regiones de restricción para la regresión de lazo y cresta.

Lasso puede establecer coeficientes en cero, mientras que la regresión de crestas superficialmente similar no puede. Esto se debe a la diferencia en la forma de sus límites de restricción. Tanto la regresión de lazo como la de cresta se pueden interpretar como una minimización de la misma función objetivo.

${\displaystyle \min _{\beta _{0},\beta }\left\{{\frac {1}{N}}\left\|y-\beta _{0}-X\beta \right\|_{2}^{2}\right\}}$

pero con respecto a diferentes restricciones: para lazo y para cresta. La figura muestra que la región de restricción definida por la norma es un cuadrado girado de modo que sus esquinas se encuentran en los ejes (en general, un politopo cruzado ), mientras que la región definida por la norma es un círculo (en general, una n -esfera ). , que es rotacionalmente invariante y, por tanto, no tiene esquinas. Como se ve en la figura, es probable que un objeto convexo que se encuentra tangente al límite, como la línea que se muestra, encuentre una esquina (o un equivalente de dimensiones superiores) de un hipercubo, para el cual algunos componentes de son idénticamente cero, mientras que en el caso de una n -esfera, los puntos en el límite para los cuales algunos de los componentes de son cero no se distinguen de los demás y no es más probable que el objeto convexo entre en contacto con un punto en el que algunos componentes de son cero que uno. para lo cual ninguno de ellos lo es. ${\displaystyle \|\beta \|_{1}\leq t}$ ${\displaystyle \|\beta \|_{2}^{2}\leq t}$ ${\displaystyle \ell ^{1}}$ ${\displaystyle \ell ^{2}}$ ${\displaystyle \beta }$ ${\displaystyle \beta }$ ${\displaystyle \beta }$

Hacer que λ sea más fácil de interpretar con una compensación entre precisión y simplicidad

El lazo se puede cambiar de escala para que sea fácil anticipar e influir en el grado de contracción asociado con un valor determinado de . ^[8] Se supone que está estandarizado con puntuaciones z y que está centrado (media cero). Representemos los coeficientes de regresión hipotéticos y hagamos referencia a las soluciones de mínimos cuadrados ordinarios optimizadas para datos. Luego podemos definir el lagrangiano como una compensación entre la precisión en la muestra de las soluciones optimizadas para datos y la simplicidad de ceñirse a los valores hipotéticos. ^[9] Esto resulta en ${\displaystyle \lambda }$ ${\displaystyle X}$ ${\displaystyle y}$ ${\displaystyle \beta _{0}}$ ${\displaystyle b_{\text{OLS}}}$

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {(y-X\beta )'(y-X\beta )}{(y-X\beta _{0})'(y-X\beta _{0})}}+2\lambda \sum _{i=1}^{p}{\frac {|\beta _{i}-\beta _{0,i}|}{q_{i}}}\right\}}$

donde se especifica a continuación y el símbolo "principal" significa transposición. La primera fracción representa una precisión relativa, la segunda fracción una simplicidad relativa y un equilibrio entre las dos. ${\displaystyle q_{i}}$ ${\displaystyle \lambda }$

Rutas de solución para la norma y la norma cuando y ${\displaystyle \ell _{1}}$ ${\displaystyle \ell _{2}}$ ${\displaystyle b_{\text{OLS}}=2}$ ${\displaystyle \beta _{0}=0}$

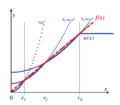
Dado un único regresor, la simplicidad relativa se puede definir especificando como , que es la cantidad máxima de desviación de cuando . Suponiendo que , la ruta de solución se puede definir en términos de : ${\displaystyle q_{i}}$ ${\displaystyle |b_{\text{OLS}}-\beta _{0}|}$ ${\displaystyle \beta _{0}}$ ${\displaystyle \lambda =0}$ ${\displaystyle \beta _{0}=0}$ ${\displaystyle R^{2}}$

${\displaystyle b_{\ell _{1}}={\begin{cases}(1-\lambda /R^{2})b_{\text{OLS}}&{\mbox{if }}\lambda \leq R^{2},\\0&{\mbox{if }}\lambda >R^{2}.\end{cases}}}$

Si , se utiliza la solución de mínimos cuadrados ordinarios (MCO). El valor hipotético de se selecciona si es mayor que . Además, si , entonces representa la influencia proporcional de . En otras palabras, mide en términos porcentuales la cantidad mínima de influencia del valor hipotético en relación con la solución OLS optimizada para datos. ${\displaystyle \lambda =0}$ ${\displaystyle \beta _{0}=0}$ ${\displaystyle \lambda }$ ${\displaystyle R^{2}}$ ${\displaystyle R^{2}=1}$ ${\displaystyle \lambda }$ ${\displaystyle \beta _{0}=0}$ ${\displaystyle \lambda \times 100\%}$

Si se utiliza una norma para penalizar las desviaciones de cero dado un único regresor, la ruta de solución viene dada por ${\displaystyle \ell _{2}}$

${\displaystyle b_{\ell _{2}}={\bigg (}1+{\frac {\lambda }{R^{2}(1-\lambda )}}{\bigg )}^{-1}b_{\text{OLS}}}$. Como , se mueve en la dirección del punto cuando está cerca de cero; pero a diferencia de , la influencia de disminuye si aumenta (ver figura). Dados múltiples regresores, el momento en que se activa un parámetro (es decir, se le permite desviarse de ) también está determinado por la contribución de un regresor a la precisión. Primero, ${\displaystyle b_{\ell _{1}}}$ ${\displaystyle b_{\ell _{2}}}$ ${\displaystyle (\lambda =R^{2},b=0)}$ ${\displaystyle \lambda }$ ${\displaystyle b_{\ell _{1}}}$ ${\displaystyle R^{2}}$ ${\displaystyle b_{\ell _{2}}}$ ${\displaystyle \lambda }$
${\displaystyle \beta _{0}}$ ${\displaystyle R^{2}}$

${\displaystyle R^{2}=1-{\frac {(y-Xb)'(y-Xb)}{(y-X\beta _{0})'(y-X\beta _{0})}}.}$

Un valor del 75% significa que la precisión en la muestra mejora en un 75% si se utilizan soluciones OLS sin restricciones en lugar de los valores hipotéticos. La contribución individual de desviarse de cada hipótesis se puede calcular con la matriz x ${\displaystyle R^{2}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle p}$ ${\displaystyle p}$

${\displaystyle R^{\otimes }=(X'{\tilde {y}}_{0})(X'{\tilde {y}}_{0})'(X'X)^{-1}({\tilde {y}}_{0}'{\tilde {y}}_{0})^{-1},}$

dónde . Si se calcula cuando , entonces los elementos diagonales de la suma son . Los valores de la diagonal pueden ser menores que 0 o, con menos frecuencia, mayores que 1. Si los regresores no están correlacionados, entonces el elemento diagonal de simplemente corresponde al valor entre y . ${\displaystyle {\tilde {y}}_{0}=y-X\beta _{0}}$ ${\displaystyle b=b_{\text{OLS}}}$ ${\displaystyle R^{2}}$ ${\displaystyle R^{\otimes }}$ ${\displaystyle R^{2}}$ ${\displaystyle R^{\otimes }}$ ${\displaystyle i^{th}}$ ${\displaystyle R^{\otimes }}$ ${\displaystyle r^{2}}$ ${\displaystyle x_{i}}$ ${\displaystyle y}$

Se puede obtener una versión reescalada del lazo adaptativo configurando . ^[10] Si los regresores no están correlacionados, el momento en que se activa el parámetro viene dado por el elemento diagonal de . Suponiendo por conveniencia que es un vector de ceros, ${\displaystyle q_{{\mbox{adaptive lasso}},i}=|b_{{\text{OLS}},i}-\beta _{0,i}|}$ ${\displaystyle i^{th}}$ ${\displaystyle i^{th}}$ ${\displaystyle R^{\otimes }}$ ${\displaystyle \beta _{0}}$

${\displaystyle b_{i}={\begin{cases}(1-\lambda /R_{ii}^{\otimes })b_{{\text{OLS}},i}&{\mbox{if }}\lambda \leq R_{ii}^{\otimes },\\0&{\mbox{if }}\lambda >R_{ii}^{\otimes }.\end{cases}}}$

Es decir, si los regresores no están correlacionados, nuevamente especifica la influencia mínima de . Incluso cuando los regresores están correlacionados, la primera vez que se activa un parámetro de regresión ocurre cuando es igual al elemento diagonal más alto de . ${\displaystyle \lambda }$ ${\displaystyle \beta _{0}}$ ${\displaystyle \lambda }$ ${\displaystyle R^{\otimes }}$

Estos resultados se pueden comparar con una versión reescalada del lazo definiendo cuál es la desviación absoluta promedio de . Suponiendo que los regresores no están correlacionados, entonces el momento de activación del regresor viene dado por ${\displaystyle q_{{\mbox{lasso}},i}={\frac {1}{p}}\sum _{l}|b_{{\text{OLS}},l}-\beta _{0,l}|}$ ${\displaystyle b_{\text{OLS}}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle i^{th}}$

${\displaystyle {\tilde {\lambda }}_{{\text{lasso}},i}={\frac {1}{p}}{\sqrt {R_{i}^{\otimes }}}\sum _{l=1}^{p}{\sqrt {R_{l}^{\otimes }}}.}$

Porque , el momento de activación vuelve a estar dado por . Si es un vector de ceros y un subconjunto de parámetros relevantes son igualmente responsables de un ajuste perfecto de , entonces este subconjunto se activa en un valor de . El momento de activación de un regresor relevante es entonces igual a . En otras palabras, la inclusión de regresores irrelevantes retrasa el momento en que este lazo reescalado activa los regresores relevantes. El lazo adaptativo y el lazo son casos especiales de un estimador '1ASTc'. Este último solo agrupa parámetros si la correlación absoluta entre los regresores es mayor que un valor especificado por el usuario. ^[8] ${\displaystyle p=1}$ ${\displaystyle {\tilde {\lambda }}_{{\text{lasso}},i}=R^{2}}$ ${\displaystyle \beta _{0}}$ ${\displaystyle p_{B}}$ ${\displaystyle R^{2}=1}$ ${\displaystyle \lambda }$ ${\displaystyle {\frac {1}{p}}}$ ${\displaystyle {\frac {1}{p}}{\frac {1}{\sqrt {p_{B}}}}p_{B}{\frac {1}{\sqrt {p_{B}}}}={\frac {1}{p}}}$

Interpretación bayesiana

Las distribuciones de Laplace tienen un pico pronunciado en su media y allí se concentra más densidad de probabilidad en comparación con una distribución normal.

Así como la regresión de cresta se puede interpretar como una regresión lineal a la que a los coeficientes se les han asignado distribuciones previas normales , el lazo se puede interpretar como una regresión lineal a la que los coeficientes tienen distribuciones previas de Laplace . La distribución de Laplace tiene un pico pronunciado en cero (su primera derivada es discontinua en cero) y concentra su masa de probabilidad más cerca de cero que la distribución normal. Esto proporciona una explicación alternativa de por qué el lazo tiende a establecer algunos coeficientes en cero, mientras que la regresión de cresta no lo hace. ^[2]

Interpretación de la relajación convexa.

Lasso también puede verse como una relajación convexa del problema de regresión de selección del mejor subconjunto, que consiste en encontrar el subconjunto de covariables que da como resultado el valor más pequeño de la función objetivo para algunos fijos , donde n es el número total de covariables. La " norma ", (el número de entradas distintas de cero de un vector), es el caso límite de " normas ", de la forma (donde las comillas significan que en realidad no son normas para ya que no es convexa para , por lo que la la desigualdad del triángulo no se cumple). Por lo tanto, dado que p = 1 es el valor más pequeño para el cual la " norma" es convexa (y por lo tanto realmente una norma), lazo es, en cierto sentido, la mejor aproximación convexa al mejor problema de selección de subconjuntos, ya que la región definida por es el casco convexo de la región definida por para . ${\displaystyle \leq k}$ ${\displaystyle k\leq n}$ ${\displaystyle \ell ^{0}}$ ${\displaystyle \|\cdot \|_{0}}$ ${\displaystyle \ell ^{p}}$ ${\displaystyle \textstyle \|x\|_{p}=\left(\sum _{i=1}^{n}|x_{j}|^{p}\right)^{1/p}}$ ${\displaystyle p<1}$ ${\displaystyle \|\cdot \|_{p}}$ ${\displaystyle p<1}$ ${\displaystyle \ell ^{p}}$ ${\displaystyle \|x\|_{1}\leq t}$ ${\displaystyle \|x\|_{p}\leq t}$ ${\displaystyle p<1}$

Generalizaciones

Se han creado variantes de Lasso para remediar las limitaciones de la técnica original y hacer que el método sea más útil para problemas particulares. Casi todos ellos se centran en respetar o explotar las dependencias entre las covariables.

La regularización de red elástica agrega una penalización adicional similar a la regresión de cresta que mejora el rendimiento cuando el número de predictores es mayor que el tamaño de la muestra, permite que el método seleccione variables fuertemente correlacionadas juntas y mejora la precisión general de la predicción. ^[7]

El lazo de grupo permite seleccionar grupos de covariables relacionadas como una sola unidad, lo que puede resultar útil en entornos donde no tiene sentido incluir algunas covariables sin otras. ^[11] Otras extensiones del lazo de grupo realizan la selección de variables dentro de grupos individuales (lazo de grupo disperso) y permiten la superposición entre grupos (lazo de grupo superpuesto). ^{[12] [13]}

El lazo fusionado puede dar cuenta de las características espaciales o temporales de un problema, lo que da como resultado estimaciones que coinciden mejor con la estructura del sistema. ^[14] Los modelos regularizados con lazo se pueden ajustar utilizando técnicas que incluyen métodos de subgradiente , regresión de ángulo mínimo (LARS) y métodos de gradiente proximal . Determinar el valor óptimo para el parámetro de regularización es una parte importante para garantizar que el modelo funcione bien; normalmente se elige mediante validación cruzada .

Red elástica

En 2005, Zou y Hastie introdujeron la red elástica . ^[7] Cuando p  >  n (el número de covariables es mayor que el tamaño de la muestra), Lasso puede seleccionar solo n covariables (incluso cuando hay más asociadas con el resultado) y tiende a seleccionar una covariable de cualquier conjunto de covariables altamente correlacionadas. Además, incluso cuando n  >  p , la regresión de crestas tiende a funcionar mejor dadas covariables fuertemente correlacionadas.

La red elástica extiende el lazo añadiendo un término de penalización adicional dando ${\displaystyle \ell ^{2}}$

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{\left\|y-X\beta \right\|_{2}^{2}+\lambda _{1}\|\beta \|_{1}+\lambda _{2}\|\beta \|_{2}^{2}\right\},}$

lo que equivale a resolver

${\displaystyle {\begin{aligned}\min _{\beta _{0},\beta }\left\{\left\|y-\beta _{0}-X\beta \right\|_{2}^{2}\right\}&{\text{ subject to }}(1-\alpha )\|\beta \|_{1}+\alpha \|\beta \|_{2}^{2}\leq t,\\&{\text{ where }}\alpha ={\frac {\lambda _{2}}{\lambda _{1}+\lambda _{2}}}.\end{aligned}}}$

Este problema se puede escribir en forma de lazo simple.

${\displaystyle \min _{\beta ^{*}\in \mathbb {R} ^{p}}\left\{\left\|y^{*}-X^{*}\beta ^{*}\right\|_{2}^{2}+\lambda ^{*}\|\beta ^{*}\|_{1}\right\}}$

dejando

${\displaystyle X_{(n+p)\times p}^{*}=(1+\lambda _{2})^{-1/2}{\binom {X}{\lambda _{2}^{1/2}I_{p\times p}}}}$,   ,   ${\displaystyle y_{(n+p)}^{*}={\binom {y}{0^{p}}},\qquad \lambda ^{*}={\frac {\lambda _{1}}{\sqrt {1+\lambda _{2}}}}}$ ${\displaystyle \beta ^{*}={\sqrt {1+\lambda _{2}}}\beta .}$

Entonces , que, cuando las covariables son ortogonales entre sí, da ${\displaystyle {\hat {\beta }}={\frac {{\hat {\beta }}^{*}}{\sqrt {1+\lambda _{2}}}}}$

${\displaystyle {\hat {\beta }}_{j}={\frac {{\hat {\beta }}{}_{j}^{\!\;*,{\text{OLS}}}}{\sqrt {1+\lambda _{2}}}}\max {\Biggl (}0,1-{\frac {\lambda ^{*}}{{\bigl |}{\hat {\beta }}{}_{j}^{\!\;*,{\text{OLS}}}{\bigr |}}}{\Biggr )}={\frac {{\hat {\beta }}{}_{j}^{\!\;{\text{OLS}}}}{1+\lambda _{2}}}\max {\Biggl (}0,1-{\frac {\lambda _{1}}{{\bigl |}{\hat {\beta }}{}_{j}^{\!\;{\text{OLS}}}{\bigr |}}}{\Biggr )}=(1+\lambda _{2})^{-1}{\hat {\beta }}{}_{j}^{\text{lasso}}.}$

Entonces, el resultado de la penalización de la red elástica es una combinación de los efectos de las penalizaciones de lazo y cresta.

Volviendo al caso general, el hecho de que la función de penalización ahora sea estrictamente convexa significa que si , , lo cual es un cambio de lazo. ^[7] En general, si ${\displaystyle x_{(j)}=x_{(k)}}$ ${\displaystyle {\hat {\beta }}_{j}={\hat {\beta }}_{k}}$ ${\displaystyle {\hat {\beta }}_{j}{\hat {\beta _{k}}}>0}$

${\displaystyle {\frac {|{\hat {\beta }}_{j}-{\hat {\beta _{k}}}|}{\|y\|}}\leq \lambda _{2}^{-1}{\sqrt {2(1-\rho _{jk})}},{\text{ where }}\rho =X^{t}X,}$

es la matriz de correlación de la muestra porque las 's están normalizadas. ${\displaystyle x}$

Por lo tanto, las covariables altamente correlacionadas tienden a tener coeficientes de regresión similares, y el grado de similitud depende tanto de como de , que es diferente de lazo. Este fenómeno, en el que covariables fuertemente correlacionadas tienen coeficientes de regresión similares, se denomina efecto de agrupación. La agrupación es deseable ya que, en aplicaciones como vincular genes a una enfermedad, es preferible encontrar todas las covariables asociadas, en lugar de seleccionar una de cada conjunto de covariables correlacionadas, como suele hacer lasso. ^[7] Además, seleccionar solo uno de cada grupo generalmente resulta en un mayor error de predicción, ya que el modelo es menos robusto (razón por la cual la regresión de crestas a menudo supera al lazo). ${\displaystyle \|y\|_{1}}$ ${\displaystyle \lambda _{2}}$

Lazo de grupo

En 2006, Yuan y Lin introdujeron el lazo de grupo para permitir que grupos predefinidos de covariables se seleccionen conjuntamente dentro o fuera de un modelo. ^[11] Esto es útil en muchos entornos, quizás más obviamente cuando una variable categórica se codifica como una colección de covariables binarias. En este caso, el lazo de grupo puede garantizar que todas las variables que codifican la covariable categórica se incluyan o excluyan juntas. Otro entorno en el que la agrupación es natural es en los estudios biológicos. Dado que los genes y las proteínas a menudo se encuentran en vías conocidas, qué vías están relacionadas con un resultado puede ser más importante que si los genes individuales lo están. La función objetivo del lazo grupal es una generalización natural del objetivo del lazo estándar.

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}{\biggl \{}{\biggl \|}y-\sum _{j=1}^{J}X_{j}\beta _{j}{\biggr \|}_{2}^{2}+\lambda \sum _{j=1}^{J}\|\beta _{j}\|_{K_{j}}{\biggr \}},\qquad \|z\|_{K_{j}}=(z^{t}K_{j}z)^{1/2}}$

donde la matriz de diseño y el vector de covariables han sido reemplazados por una colección de matrices de diseño y vectores de covariables , uno para cada uno de los J grupos. Además, el término de penalización es ahora una suma de las normas definidas por las matrices definidas positivas . Si cada covariable está en su propio grupo y , entonces esto se reduce al lazo estándar, mientras que si solo hay un grupo y , se reduce a la regresión de cresta. Dado que la penalización se reduce a una norma en los subespacios definidos por cada grupo, no puede seleccionar sólo algunas de las covariables de un grupo, al igual que la regresión de crestas no puede hacerlo. Sin embargo, debido a que la penalización es la suma de las diferentes normas del subespacio, como en el lazo estándar, la restricción tiene algunos puntos no diferenciales, que corresponden a que algunos subespacios sean idénticamente cero. Por lo tanto, puede establecer los vectores de coeficientes correspondientes a algunos subespacios en cero, mientras que otros solo se reducen. Sin embargo, es posible extender el lazo de grupo al llamado lazo de grupo disperso, que puede seleccionar covariables individuales dentro de un grupo, agregando una penalización adicional a cada subespacio de grupo. ^[12] Otra extensión, el lazo de grupo con superposición, permite compartir covariables entre grupos, por ejemplo, si un gen apareciera en dos vías. ^[13] ${\displaystyle X}$ ${\displaystyle \beta }$ ${\displaystyle X_{j}}$ ${\displaystyle \beta _{j}}$ ${\displaystyle \ell ^{2}}$ ${\displaystyle K_{j}}$ ${\displaystyle K_{j}=I}$ ${\displaystyle K_{1}=I}$ ${\displaystyle \ell ^{2}}$ ${\displaystyle \ell ^{1}}$

El paquete "gglasso" de R, permite una implementación rápida y eficiente de Group LASSO. ^[15]

Lazo fusionado

En algunos casos, el fenómeno bajo estudio puede tener una estructura espacial o temporal importante que debe considerarse durante el análisis, como series de tiempo o datos basados ​​en imágenes. En 2005, Tibshirani y sus colegas introdujeron el lazo fusionado para extender su uso a este tipo de datos. ^[14] La función objetivo del lazo fusionado es

${\displaystyle {\begin{aligned}&\min _{\beta }{\biggl \{}{\frac {1}{N}}\sum _{i=1}^{N}\left(y_{i}-x_{i}^{T}\beta \right)^{2}{\biggr \}}\\[4pt]&{\text{ subject to }}\sum _{j=1}^{p}|\beta _{j}|\leq t_{1}{\text{ and }}\sum _{j=2}^{p}|\beta _{j}-\beta _{j-1}|\leq t_{2}.\end{aligned}}}$

La primera restricción es la restricción del lazo, mientras que la segunda penaliza directamente los grandes cambios con respecto a la estructura temporal o espacial, lo que obliga a los coeficientes a variar suavemente para reflejar la lógica subyacente del sistema. El lazo agrupado ^[16] es una generalización del lazo fusionado que identifica y agrupa covariables relevantes en función de sus efectos (coeficientes). La idea básica es penalizar las diferencias entre los coeficientes para que los distintos de cero se agrupen. Esto se puede modelar utilizando la siguiente regularización:

${\displaystyle \sum _{i<j}^{p}|\beta _{i}-\beta _{j}|\leq t_{2}.}$

Por el contrario, las variables se pueden agrupar en grupos altamente correlacionados y luego se puede extraer una única covariable representativa de cada grupo. ^[17]

Existen algoritmos que resuelven el problema del lazo fusionado y algunas generalizaciones del mismo. Los algoritmos pueden resolverlo exactamente en un número finito de operaciones. ^[18]

Cuasi-normas y regresión puente

Un ejemplo de función potencial PQSQ (función cuadrática por partes de crecimiento subcuadrático) ; aquí la función mayor es ; el potencial se define con recorte después . ${\displaystyle u(x)}$ ${\displaystyle f(x)=x}$ ${\displaystyle r_{3}}$

Un ejemplo de cómo funciona la regresión regularizada PQSQ eficiente es como -norm lazo. ^[19] ${\displaystyle \ell ^{1}}$

Lazo, red elástica, grupo y lazo fusionado construyen las funciones de penalización a partir de las normas y (con pesos, si es necesario). La regresión puente utiliza normas generales ( ) y cuasinormas ( ). ^[20] Por ejemplo, para p =1/2 el análogo del objetivo del lazo en la forma lagrangiana es resolver ${\displaystyle \ell ^{1}}$ ${\displaystyle \ell ^{2}}$ ${\displaystyle \ell ^{p}}$ ${\displaystyle p\geq 1}$ ${\displaystyle 0<p<1}$

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\|y-X\beta \right\|_{2}^{2}+\lambda {\sqrt {\|\beta \|_{1/2}}}\right\},}$

dónde

${\displaystyle \|\beta \|_{1/2}={\biggl (}\sum _{j=1}^{p}{\sqrt {|\beta _{j}|}}{\biggr )}^{2}}$

Se afirma que las cuasi-normas fraccionarias ( ) proporcionan resultados más significativos en el análisis de datos tanto teórica como empíricamente. ^[21] La no convexidad de estas cuasi-normas complica el problema de optimización. Para resolver este problema, se desarrolla un procedimiento de minimización de expectativas ^[22] e implementa ^[19] para minimizar la función ${\displaystyle \ell ^{p}}$ ${\displaystyle 0<p<1}$

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\|y-X\beta \right\|_{2}^{2}+\lambda \sum _{j=1}^{p}\vartheta (\beta _{j}^{2})\right\},}$

donde es una función cóncava arbitraria que aumenta monótonamente (por ejemplo, da la penalización del lazo y da la penalización). ${\displaystyle \vartheta (\gamma )}$ ${\displaystyle \vartheta (\gamma )={\sqrt {\gamma }}}$ ${\displaystyle \vartheta (\gamma )=\gamma ^{1/4}}$ ${\displaystyle \ell ^{1/2}}$

El algoritmo eficiente para la minimización se basa en la aproximación cuadrática por partes del crecimiento subcuadrático (PQSQ). ^[22]

Lazo adaptativo

El lazo adaptativo fue introducido por Zou en 2006 para la regresión lineal ^[23] y por Zhang y Lu en 2007 para la regresión de riesgos proporcionales. ^[24]

lazo previo

El lazo anterior fue introducido para modelos lineales generalizados por Jiang et al. en 2016 para incorporar información previa, como la importancia de determinadas covariables. ^[25] En el lazo previo, dicha información se resume en pseudorespuestas (llamadas respuestas previas) y luego se agrega una función de criterio adicional a la función objetivo habitual con una penalización de lazo. Sin pérdida de generalidad, en regresión lineal, la nueva función objetivo se puede escribir como ${\displaystyle {\hat {y}}^{\mathrm {p} }}$

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\|y-X\beta \right\|_{2}^{2}+{\frac {1}{N}}\eta \left\|{\hat {y}}^{\mathrm {p} }-X\beta \right\|_{2}^{2}+\lambda \|\beta \|_{1}\right\},}$

que es equivalente a

${\displaystyle \min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\|{\tilde {y}}-X\beta \right\|_{2}^{2}+{\frac {\lambda }{1+\eta }}\|\beta \|_{1}\right\},}$

la función objetivo de lazo habitual con las respuestas reemplazadas por un promedio ponderado de las respuestas observadas y las respuestas anteriores (llamadas valores de respuesta ajustados por la información anterior). ${\displaystyle y}$ ${\displaystyle {\tilde {y}}=(y+\eta {\hat {y}}^{\mathrm {p} })/(1+\eta )}$

En lazo anterior, el parámetro se denomina parámetro de equilibrio, ya que equilibra la importancia relativa de los datos y la información previa. En el caso extremo de , el lazo anterior se reduce a lazo. Si es así , el lazo anterior se basará únicamente en la información anterior para ajustarse al modelo. Además, el parámetro de equilibrio tiene otra interpretación atractiva: controla la varianza de en su distribución previa desde un punto de vista bayesiano. ${\displaystyle \eta }$ ${\displaystyle \eta =0}$ ${\displaystyle \eta =\infty }$ ${\displaystyle \eta }$ ${\displaystyle \beta }$

El lazo previo es más eficiente en la estimación y predicción de parámetros (con un error de estimación y un error de predicción más pequeños) cuando la información previa es de alta calidad y es robusto a la información previa de baja calidad con una buena elección del parámetro de equilibrio . ${\displaystyle \eta }$

Soluciones informáticas de lazo

La función de pérdida del lazo no es diferenciable, pero se ha desarrollado una amplia variedad de técnicas de análisis convexo y teoría de optimización para calcular la ruta de solución del lazo. Estos incluyen descenso de coordenadas, ^[26] métodos de subgradiente, regresión de ángulo mínimo (LARS) y métodos de gradiente proximal. ^{[27] Los métodos} de subgradiente son la generalización natural de métodos tradicionales como el descenso de gradiente y el descenso de gradiente estocástico para el caso en el que la función objetivo no es diferenciable en todos los puntos. LARS es un método estrechamente vinculado a los modelos de lazo y, en muchos casos, permite ajustarlos de manera eficiente, aunque es posible que no funcione bien en todas las circunstancias. LARS genera rutas de solución completas. ^[27] Los métodos proximales se han vuelto populares debido a su flexibilidad y rendimiento y son un área de investigación activa. La elección del método dependerá de la variante particular del lazo, los datos y los recursos disponibles. Sin embargo, los métodos proximales generalmente funcionan bien.

El paquete "glmnet" en R, donde "glm" es una referencia a "modelos lineales generalizados" y "net" se refiere a la "red" de "elastic net" proporciona una forma extremadamente eficiente de implementar LASSO y algunas de sus variantes. ^{[28] [29] [30]}

Elección del parámetro de regularización

Elegir el parámetro de regularización ( ) es una parte fundamental de Lasso. Un buen valor es esencial para el rendimiento de Lasso, ya que controla la fuerza de la contracción y la selección de variables, lo que, con moderación, puede mejorar tanto la precisión de la predicción como la interpretabilidad. Sin embargo, si la regularización se vuelve demasiado fuerte, es posible que se omitan variables importantes y que los coeficientes se reduzcan excesivamente, lo que puede perjudicar tanto la capacidad predictiva como la inferencia. La validación cruzada se utiliza a menudo para encontrar el parámetro de regularización. ${\displaystyle \lambda }$

Los criterios de información como el criterio de información bayesiano (BIC) y el criterio de información de Akaike (AIC) podrían ser preferibles a la validación cruzada, porque son más rápidos de calcular y su rendimiento es menos volátil en muestras pequeñas. ^[31] Un criterio de información selecciona el parámetro de regularización del estimador maximizando la precisión en la muestra de un modelo mientras penaliza su número efectivo de parámetros/grados de libertad. Zou et al. propuso medir los grados de libertad efectivos contando el número de parámetros que se desvían de cero. ^{[32] Kaufman y Rosset [33]} y Janson et al., ^[34] consideraron que el enfoque de grados de libertad era defectuoso porque los grados de libertad de un modelo podrían aumentar incluso cuando el parámetro de regularización lo penaliza más severamente. Como alternativa, se puede utilizar la medida de simplicidad relativa definida anteriormente para contar el número efectivo de parámetros. ^[31] Para el lazo, esta medida viene dada por

${\displaystyle {\hat {\mathcal {P}}}=\sum _{i=1}^{p}{\frac {|\beta _{i}-\beta _{0,i}|}{{\frac {1}{p}}\sum _{l}|b_{{\text{OLS}},l}-\beta _{0,l}|}}}$,

que aumenta monótonamente de cero a medida que el parámetro de regularización disminuye de cero. ${\displaystyle p}$ ${\displaystyle \infty }$

Aplicaciones seleccionadas

LASSO se ha aplicado en economía y finanzas, y se descubrió que mejora la predicción y selecciona variables a veces ignoradas, por ejemplo en la literatura de predicción de quiebras corporativas ^[35] o en la predicción de empresas de alto crecimiento. ^[36]

Ver también

• Desviaciones mínimas absolutas
• Selección de modelo
• Regresión no paramétrica
• Regularización de Tikhonov

Referencias

1. Santosa, Fadil; Symes, William W. (1986). "Inversión lineal de sismogramas de reflexión de banda limitada". Revista SIAM de Computación Científica y Estadística . SIAM. 7 (4): 1307-1330. doi :10.1137/0907087.
2. Tibshirani, Robert (1996). "Regresión, contracción y selección mediante el lazo". Revista de la Real Sociedad de Estadística . Serie B (metodológica). Wiley. 58 (1): 267–88. JSTOR  2346178.
3. Tibshirani, Robert (1997). "El método del lazo para la selección de variables en el modelo de Cox". Estadística en Medicina . 16 (4): 385–395. CiteSeerX 10.1.1.411.8024 . doi :10.1002/(SICI)1097-0258(19970228)16:4<385::AID-SIM380>3.0.CO;2-3. PMID  9044528. 
4. Breiman, Leo (1995). "Mejor regresión de subconjuntos utilizando el garrote no negativo". Tecnometría . 37 (4): 373–84. doi :10.1080/00401706.1995.10484371.
5. McDonald, Gary (2009). "Regresión de crestas". Revisiones interdisciplinarias de Wiley: estadística computacional . 1 : 93–100. doi :10.1002/wics.14. S2CID  64699223 . Consultado el 22 de agosto de 2022 .
6. Melkumová, LE; Shatskikh, S. Ya. (01/01/2017). "Comparación de estimadores Ridge y LASSO para el análisis de datos". Ingeniería de Procedia . Tercera Conferencia Internacional “Tecnología de la información y nanotecnología”, ITNT-2017, 25 a 27 de abril de 2017, Samara, Rusia. 201 : 746–755. doi : 10.1016/j.proeng.2017.09.615 . ISSN  1877-7058.
7. Zou, Hui; Hastie, Trevor (2005). "Regularización y selección de variables a través de la red elástica". Revista de la Real Sociedad de Estadística . Serie B (Metodología estadística). Wiley. 67 (2): 301–20. doi : 10.1111/j.1467-9868.2005.00503.x . JSTOR  3647580. S2CID  122419596.
8. Hoornweg, Víctor (2018). "Capítulo 8". Ciencia: bajo presentación . Prensa Hoornweg. ISBN 978-90-829188-0-9.
9. Motamedi, Fahimeh; Sánchez, Horacio; Mehri, Alireza; Ghasemi, Fahimeh (octubre de 2021). "Acelerar el análisis de Big Data mediante el algoritmo forestal aleatorio LASSO en estudios QSAR". Bioinformática . 37 (19): 469–475. doi : 10.1093/bioinformática/btab659. ISSN  1367-4803. PMID  34979024.
10. Zou, Hui (2006). "El lazo adaptativo y sus propiedades de Oracle" (PDF) .
11. Yuan, Ming; Lin, Yi (2006). "Selección y estimación de modelos en regresión con variables agrupadas". Revista de la Real Sociedad de Estadística . Serie B (Metodología estadística). Wiley. 68 (1): 49–67. doi : 10.1111/j.1467-9868.2005.00532.x . JSTOR  3647556. S2CID  6162124.
12. Puig, Arnau Tibau, Ami Wiesel y Alfred O. Hero III. "Un operador multidimensional de umbral de contracción". Actas del decimoquinto taller sobre procesamiento estadístico de señales, SSP'09, IEEE, págs.
13. Jacob, Laurent, Guillaume Obozinski y Jean-Philippe Vert. "Agrupar Lasso con Superposición y Gráfico LASSO". Publicado en las actas de la 26ª Conferencia Internacional sobre Aprendizaje Automático, Montreal, Canadá, 2009.
14. Tibshirani, Robert, Michael Saunders, Saharon Rosset, Ji Zhu y Keith Knight. 2005. “Escasez y suavidad a través del lazo fusionado”. Revista de la Real Sociedad de Estadística. Serie B (Metodología estadística) 67 (1). Wiley: 91-108. https://www.jstor.org/stable/3647602.
15. Yang, Yi; Zou, Hui (noviembre de 2015). "Un algoritmo unificado rápido para resolver problemas de aprendizaje de penalización de lazo grupal". Estadística y Computación . 25 (6): 1129-1141. doi :10.1007/s11222-014-9498-5. ISSN  0960-3174. S2CID  255072855.
16. Ella, Yiyuan (2010). "Regresión escasa con agrupamiento exacto". Revista Electrónica de Estadística . 4 : 1055-1096. doi : 10.1214/10-EJS578 .
17. Reid, Stephen (2015). "Regresión escasa y pruebas marginales utilizando prototipos de clúster". Bioestadística . 17 (2): 364–76. arXiv : 1503.00334 . Código Bib : 2015arXiv150300334R. doi : 10.1093/bioestadística/kxv049. PMC 5006118 . PMID  26614384. 
18. Bento, José (2018). "Sobre la complejidad del lazo fusionado ponderado". Letras IEEE en procesamiento de señales . 25 (10): 1595-1599. arXiv : 1801.04987 . Código Bib : 2018ISPL...25.1595B. doi :10.1109/LSP.2018.2867800. S2CID  5008891.
19. Repositorio de regresión regularizada Mirkes EM PQSQ, GitHub.
20. Fu, Wenjiang J. 1998. “El puente versus el lazo”. Revista de Estadística Computacional y Gráfica 7 (3). Taylor y Francisco: 397-416.
21. Aggarwal CC, Hinneburg A., Keim DA (2001) "Sobre el comportamiento sorprendente de las métricas de distancia en un espacio de alta dimensión". En: Van den Bussche J., Vianu V. (eds) Teoría de bases de datos - ICDT 2001. ICDT 2001. Lecture Notes in Computer Science, vol. 1973. Springer, Berlín, Heidelberg, págs. 420-434.
22. Gorban, AN; Mirkes, EM; Zinovyev, A. (2016) "Aproximaciones cuadráticas por partes de funciones de error arbitrarias para un aprendizaje automático rápido y robusto". Redes neuronales, 84, 28-38.
23. Zou (2006, JASA)
24. Zhang y Lu (2007, Biometrika)
25. Jiang, Yuan (2016). "Selección de variables con información previa para modelos lineales generalizados mediante el método del lazo previo". Revista de la Asociación Estadounidense de Estadística . 111 (513): 355–376. doi :10.1080/01621459.2015.1008363. PMC 4874534 . PMID  27217599. 
26. Jerome Friedman, Trevor Hastie y Robert Tibshirani. 2010. “Rutas de regularización para modelos lineales generalizados mediante descenso de coordenadas”. Revista de software estadístico 33 (1): 1-21. https://www.jstatsoft.org/article/view/v033i01/v33i01.pdf.
27. Efron, Bradley, Trevor Hastie, Iain Johnstone y Robert Tibshirani. 2004. “Regresión de ángulo mínimo”. Los Anales de Estadística 32 (2). Instituto de Estadística Matemática: 407–51. https://www.jstor.org/stable/3448465.
28. Friedman, Jerónimo; Hastie, Trevor; Tibshirani, Robert (2010). "Rutas de regularización para modelos lineales generalizados mediante descenso de coordenadas". Revista de software estadístico . 33 (1): 1–22. doi : 10.18637/jss.v033.i01 . ISSN  1548-7660. PMC 2929880 . PMID  20808728. 
29. Simón, Noé; Friedman, Jerome; Hastie, Trevor; Tibshirani, Rob (2011). "Rutas de regularización para el modelo de riesgos proporcionales de Cox mediante descenso de coordenadas". Revista de software estadístico . 39 (5): 1–13. doi : 10.18637/jss.v039.i05. ISSN  1548-7660. PMC 4824408 . PMID  27065756. 
30. Tay, J. Kenneth; Narasimhan, Balasubramanian; Hastie, Trevor (2023). "Rutas de regularización neta elástica para todos los modelos lineales generalizados". Revista de software estadístico . 106 (1). doi : 10.18637/jss.v106.i01 . ISSN  1548-7660. PMC 10153598 . PMID  37138589. 
31. Hoornweg, Víctor (2018). "Capítulo 9". Ciencia: bajo presentación . Prensa Hoornweg. ISBN 978-90-829188-0-9.
32. Zou, Hui; Hastie, Trevor; Tibshirani, Robert (2007). "Sobre los 'grados de libertad' del lazo". Los anales de la estadística . 35 (5): 2173–2792. doi : 10.1214/009053607000000127 .
33. Kaufman, S.; Rosset, S. (2014). "¿Cuándo más regularización implica menos grados de libertad? Condiciones y contraejemplos suficientes". Biometrika . 101 (4): 771–784. doi :10.1093/biomet/asu034. ISSN  0006-3444.
34. Janson, Lucas; Fithian, William; Hastie, Trevor J. (2015). "Grados efectivos de libertad: una metáfora defectuosa". Biometrika . 102 (2): 479–485. doi :10.1093/biomet/asv019. ISSN  0006-3444. PMC 4787623 . PMID  26977114. 
35. Shaonan, Tian; Yu, Yan; Guo, Hui (2015). "Selección de variables y previsiones de quiebra de empresas". Revista de Banca y Finanzas . 52 (1): 89-100. doi :10.1016/j.jbankfin.2014.12.003.
36. Coad, Alex; Srhoj, Stjepan (2020). "Atrapar gacelas con un lazo: técnicas de big data para la predicción de empresas de alto crecimiento". Economía de las pequeñas empresas . 55 (1): 541–565. doi :10.1007/s11187-019-00203-3. S2CID  255011751.