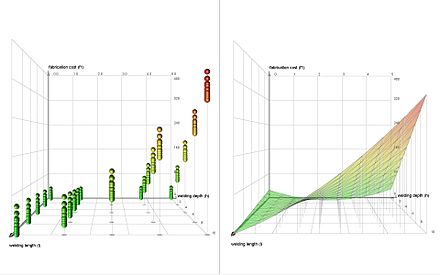
En estadística , un experimento factorial completo es un experimento cuyo diseño consta de dos o más factores, cada uno con valores posibles discretos o "niveles", y cuyas unidades experimentales adoptan todas las combinaciones posibles de estos niveles en todos esos factores. Un diseño factorial completo también puede denominarse diseño completamente cruzado . Un experimento de este tipo permite al investigador estudiar el efecto de cada factor en la variable de respuesta , así como los efectos de las interacciones entre factores en la variable de respuesta.
En la gran mayoría de los experimentos factoriales, cada factor tiene solo dos niveles. Por ejemplo, si dos factores ocupan dos niveles cada uno, un experimento factorial tendría cuatro combinaciones de tratamientos en total y suele denominarse diseño factorial 2×2 . En un diseño de este tipo, la interacción entre las variables suele ser la más importante. Esto se aplica incluso a los escenarios en los que hay un efecto principal y una interacción.
Si el número de combinaciones en un diseño factorial completo es demasiado alto para ser logísticamente factible, se puede realizar un diseño factorial fraccionado , en el que se omiten algunas de las combinaciones posibles (generalmente al menos la mitad).
A menudo se utilizan otros términos para "combinaciones de tratamientos", como ejecuciones (de un experimento), puntos (viendo las combinaciones como vértices de un gráfico ) y celdas (que surgen como intersecciones de filas y columnas).
Los diseños factoriales fueron utilizados en el siglo XIX por John Bennet Lawes y Joseph Henry Gilbert de la Estación Experimental de Rothamsted . [1]
Ronald Fisher argumentó en 1926 que los diseños "complejos" (como los diseños factoriales) eran más eficientes que estudiar un factor a la vez. [2] Fisher escribió:
"Ningún aforismo se repite con más frecuencia en relación con los ensayos de campo que el de que debemos hacerle a la Naturaleza pocas preguntas o, idealmente, una pregunta a la vez. El autor está convencido de que esta opinión es totalmente errónea. La Naturaleza, sugiere, responderá mejor a un cuestionario lógico y cuidadosamente pensado; de hecho, si le hacemos una sola pregunta, a menudo se negará a responder hasta que se haya discutido algún otro tema".
Un diseño factorial permite determinar el efecto de varios factores e incluso las interacciones entre ellos con el mismo número de ensayos que son necesarios para determinar cualquiera de los efectos por sí solo con el mismo grado de precisión.
Frank Yates hizo contribuciones significativas, particularmente en el análisis de diseños, mediante el análisis de Yates .
Es posible que el término "factorial" no haya sido utilizado en forma impresa antes de 1935, cuando Fisher lo utilizó en su libro El diseño de experimentos . [3]
Muchas personas examinan el efecto de un solo factor o variable. En comparación con los experimentos de un factor a la vez (OFAT), los experimentos factoriales ofrecen varias ventajas [4] [5]
La principal desventaja del diseño factorial completo es su requisito de tamaño de muestra, que crece exponencialmente con el número de factores o entradas consideradas. [6] Las estrategias alternativas con eficiencia computacional mejorada incluyen diseños factoriales fraccionados , muestreo de hipercubo latino y técnicas de muestreo cuasialeatorio .
En su libro, Improving Almost Anything: Ideas and Essays (Mejorar casi cualquier cosa: ideas y ensayos) , el estadístico George Box ofrece muchos ejemplos de los beneficios de los experimentos factoriales. A continuación se muestra uno de ellos. [7] Los ingenieros del fabricante de rodamientos SKF querían saber si el cambio a un diseño de "jaula" menos costoso afectaría la vida útil de los rodamientos. Los ingenieros pidieron ayuda a Christer Hellstrand, un estadístico, para diseñar el experimento. [8]
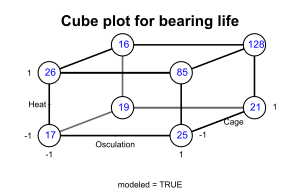
Box informa lo siguiente: "Los resultados se evaluaron mediante una prueba de vida acelerada... Las pruebas eran costosas porque debían realizarse en una línea de producción real y los experimentadores planeaban hacer cuatro pruebas con la jaula estándar y cuatro con la jaula modificada. Christer preguntó si había otros factores que les gustaría probar. Dijeron que sí, pero que hacer pruebas adicionales excedería su presupuesto. Christer les mostró cómo podían probar dos factores adicionales "gratis", sin aumentar el número de pruebas y sin reducir la precisión de su estimación del efecto de la jaula. En este arreglo, llamado diseño factorial 2×2×2, cada uno de los tres factores se ejecutaría en dos niveles y se incluirían las ocho combinaciones posibles. Las diversas combinaciones se pueden mostrar convenientemente como los vértices de un cubo..." "En cada caso, la condición estándar se indica con un signo menos y la condición modificada con un signo más. Los factores modificados fueron el tratamiento térmico, la osculación del anillo exterior y el diseño de la jaula. Los números muestran las duraciones relativas de vida de los cojinetes. "Si observamos [el diagrama cúbico], podemos ver que la elección del diseño de la jaula no tuvo mucha influencia... Pero, si promediamos los pares de números para el diseño de la jaula, obtenemos la [tabla siguiente], que muestra lo que hicieron los otros dos factores... Esto llevó al extraordinario descubrimiento de que, en esta aplicación particular, la vida útil de un rodamiento se puede quintuplicar si los dos factores, la osculación del anillo exterior y los tratamientos térmicos del anillo interior, se incrementan juntos".
"Si tenemos en cuenta que se han fabricado cojinetes como este durante décadas, resulta sorprendente que haya sido necesario tanto tiempo para descubrir una mejora tan importante. Una explicación probable es que, como hasta hace poco la mayoría de los ingenieros solo empleaban un factor a la vez en la experimentación, no se han detectado los efectos de interacción ".
El experimento factorial más simple contiene dos niveles para cada uno de los dos factores. Supongamos que un ingeniero desea estudiar la potencia total utilizada por cada uno de los dos motores diferentes, A y B, que funcionan a cada una de las dos velocidades diferentes, 2000 o 3000 RPM. El experimento factorial constaría de cuatro unidades experimentales: motor A a 2000 RPM, motor B a 2000 RPM, motor A a 3000 RPM y motor B a 3000 RPM. Cada combinación de un único nivel seleccionado de cada factor está presente una vez.
Este experimento es un ejemplo de un experimento factorial 2 2 (o 2×2), llamado así porque considera dos niveles (la base) para cada uno de dos factores (la potencia o superíndice), o #niveles #factores , produciendo 2 2 = 4 puntos factoriales.
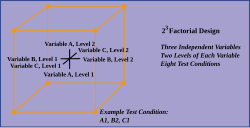
Los diseños pueden incluir muchas variables independientes. Como ejemplo adicional, se pueden evaluar los efectos de tres variables de entrada en ocho condiciones experimentales que se muestran como las esquinas de un cubo.
Esto se puede realizar con o sin replicación, según el propósito previsto y los recursos disponibles. Proporcionará los efectos de las tres variables independientes sobre la variable dependiente y las posibles interacciones.
Los experimentos factoriales se describen por dos cosas: el número de factores y el número de niveles de cada factor. Por ejemplo, un experimento factorial 2×3 tiene dos factores, el primero en 2 niveles y el segundo en 3 niveles. Tal experimento tiene 2×3=6 combinaciones de tratamiento o celdas. De manera similar, un experimento 2×2×3 tiene tres factores, dos en 2 niveles y uno en 3, para un total de 12 combinaciones de tratamiento. Si cada factor tiene s niveles (un llamado diseño de nivel fijo o simétrico ), el experimento se denota típicamente por s k , donde k es el número de factores. Por lo tanto, un experimento 2 5 tiene 5 factores, cada uno en 2 niveles. Los experimentos que no son de nivel fijo se dicen que son de nivel mixto o asimétricos .
Existen diversas tradiciones para denotar los niveles de cada factor. Si un factor ya tiene unidades naturales, se utilizan estas. Por ejemplo, un experimento de acuicultura de camarones [9] podría tener factores de temperatura a 25 °C y 35 °C, densidad a 80 o 160 camarones/40 litros y salinidad al 10 %, 25 % y 40 %. Sin embargo, en muchos casos, los niveles de los factores son simplemente categorías y la codificación de los niveles es algo arbitraria. Por ejemplo, los niveles de un factor de 6 niveles podrían simplemente denotarse como 1, 2, ..., 6.
Las combinaciones de tratamientos se indican mediante pares ordenados o, de forma más general, tuplas ordenadas . En el experimento de acuicultura, el triple ordenado (25, 80, 10) representa la combinación de tratamientos que tiene el nivel más bajo de cada factor. En un experimento general de 2x3, el par ordenado (2, 1) indicaría la celda en la que el factor A está en el nivel 2 y el factor B en el nivel 1. Los paréntesis suelen omitirse, como se muestra en la tabla adjunta.
Para denotar los niveles de factores en experimentos de 2 k , aparecen en la literatura tres sistemas particulares:
Si estos valores representan los valores "bajo" y "alto" de un tratamiento, entonces es natural que 1 represente "alto", ya sea que se utilicen 0 y 1 o −1 y 1. Esto se ilustra en la tabla adjunta para un experimento 2×2. Si los niveles de los factores son simplemente categorías, la correspondencia puede ser diferente; por ejemplo, es natural representar las condiciones "de control" y "experimentales" codificando "control" como 0 si se utilizan 0 y 1, y como 1 si se utilizan 1 y −1. [nota 1] A continuación se ofrece un ejemplo de esto último. Ese ejemplo ilustra otro uso de la codificación +1 y −1.
Para otros experimentos de nivel fijo ( s k ), los valores 0, 1, ..., s −1 se utilizan a menudo para indicar los niveles de los factores. Estos son los valores de los números enteros módulo s cuando s es primo. [nota 2]
La respuesta esperada a una combinación de tratamiento dada se denomina media celular , [12] que generalmente se denota utilizando la letra griega μ. (El término célula se toma prestado de su uso en tablas de datos ). Esta notación se ilustra aquí para el experimento 2 × 3.
Un contraste en medias de celdas es una combinación lineal de medias de celdas en la que los coeficientes suman 0. Los contrastes son de interés en sí mismos y son los bloques de construcción mediante los cuales se definen los efectos e interacciones principales.
En el experimento 2 × 3 ilustrado aquí, la expresión
es un contraste que compara las respuestas medias de las combinaciones de tratamiento 11 y 12. (Los coeficientes aquí son 1 y –1). El contraste
Se dice que pertenece al efecto principal del factor A, ya que contrasta las respuestas del nivel "1" del factor con las del nivel "2". Se dice que el efecto principal de A está ausente si esta expresión es igual a 0.
La interacción en un experimento factorial es la falta de aditividad entre factores y también se expresa mediante contrastes. En el experimento 2 × 3, los contrastes
y
pertenecen a la interacción A × B ; la interacción está ausente ( hay aditividad ) si estas expresiones son iguales a 0. [13] [14] La aditividad puede verse como un tipo de paralelismo entre factores, como se ilustra en la sección de Análisis a continuación.
Dado que los coeficientes de estos contrastes son los que contienen la información esencial, a menudo se muestran como vectores de columna . Para el ejemplo anterior, una tabla de este tipo podría verse así: [15]
Las columnas de dicha tabla se denominan vectores de contraste : sus componentes suman 0. Cada efecto está determinado tanto por el patrón de componentes en sus columnas como por el número de columnas .
Los patrones de componentes de estas columnas reflejan las definiciones generales dadas por Bose : [16]
Se aplican definiciones similares para las interacciones de más de dos factores. En el ejemplo 2 × 3, por ejemplo, el patrón de la columna A sigue el patrón de los niveles del factor A , indicado por el primer componente de cada celda.
El número de columnas necesarias para especificar cada efecto son los grados de libertad del efecto [nota 4] y es una cantidad esencial en el análisis de varianza . La fórmula es la siguiente: [18] [19]
La fórmula para más de dos factores sigue este patrón. En el ejemplo 2 × 3 anterior, los grados de libertad para los dos efectos principales y la interacción (la cantidad de columnas para cada uno) son 1, 2 y 2, respectivamente.
En las tablas de los siguientes ejemplos, las entradas de la columna "celda" son combinaciones de tratamientos: el primer componente de cada combinación es el nivel del factor A , el segundo el del factor B y el tercero (en el ejemplo 2 × 2 × 2) el nivel del factor C. Las entradas de cada una de las otras columnas suman 0, de modo que cada columna es un vector de contraste.
Un experimento 3 × 3: Aquí esperamos 3-1 = 2 grados de libertad cada uno para los efectos principales de los factores A y B , y (3-1)(3-1) = 4 grados de libertad para la interacción A × B. Esto explica la cantidad de columnas para cada efecto en la tabla adjunta.
Los dos vectores de contraste para A dependen únicamente del nivel del factor A. Esto se puede ver al notar que el patrón de entradas en cada columna A es el mismo que el patrón del primer componente de "celda". (Si es necesario, ordenar la tabla en A mostrará esto). Por lo tanto, estos dos vectores pertenecen al efecto principal de A. De manera similar, los dos vectores de contraste para B dependen únicamente del nivel del factor B , es decir, el segundo componente de "celda", por lo que pertenecen al efecto principal de B.
Los últimos cuatro vectores de columna pertenecen a la interacción A × B , ya que sus entradas dependen de los valores de ambos factores y las cuatro columnas son ortogonales a las columnas de A y B. Esto último se puede verificar tomando productos escalares .
Un experimento de 2 × 2 × 2: tendrá 1 grado de libertad para cada efecto e interacción principal. Por ejemplo, una interacción de dos factores tendrá (2-1)(2-1) = 1 grado de libertad. Por lo tanto, solo se necesita una única columna para especificar cada uno de los siete efectos.
Las columnas de A , B y C representan los efectos principales correspondientes, ya que las entradas en cada columna dependen únicamente del nivel del factor correspondiente. Por ejemplo, las entradas en la columna B siguen el mismo patrón que el componente central de la "celda", como se puede ver al ordenar por B.
Las columnas de AB , AC y BC representan las interacciones de dos factores correspondientes. Por ejemplo, (i) las entradas en la columna BC dependen del segundo y tercer componente ( B y C ) de la celda , y son independientes del primer componente ( A ), como se puede ver ordenando por BC ; y (ii) la columna BC es ortogonal a las columnas B y C , como se puede verificar calculando productos escalares.
Finalmente, la columna ABC representa la interacción de tres factores: sus entradas dependen de los niveles de los tres factores y es ortogonal a los otros seis vectores de contraste.
Combinadas y leídas fila por fila, las columnas A, B y C dan una notación alternativa, mencionada anteriormente, para las combinaciones de tratamiento (celdas) en este experimento: la celda 000 corresponde a +++, la 001 a ++−, etc.
En las columnas A a ABC , el número 1 puede reemplazarse por cualquier constante, porque las columnas resultantes seguirán siendo vectores de contraste. Por ejemplo, es común usar el número 1/4 en experimentos de 2 × 2 × 2 [nota 5] para definir cada efecto o interacción principal y para declarar, por ejemplo, que el contraste
es "el" efecto principal del factor A , una cantidad numérica que puede estimarse. [20]
Para más de dos factores, un experimento factorial de 2 k puede diseñarse recursivamente a partir de un experimento factorial de 2 k −1 replicando el experimento de 2 k −1 , asignando la primera réplica al primer nivel (o nivel bajo) del nuevo factor, y la segunda réplica al segundo nivel (o nivel alto). Este marco puede generalizarse, por ejemplo , para diseñar tres réplicas para factores de tres niveles , etc.
Un experimento factorial permite estimar el error experimental de dos maneras. El experimento puede ser replicado , o el principio de escasez de efectos puede ser explotado a menudo. La replicación es más común para experimentos pequeños y es una forma muy confiable de evaluar el error experimental. Cuando el número de factores es grande (normalmente más de 5 factores, pero esto varía según la aplicación), la replicación del diseño puede volverse operativamente difícil. En estos casos, es común ejecutar solo una única réplica del diseño y asumir que las interacciones de factores de más de un cierto orden (por ejemplo, entre tres o más factores) son insignificantes. Bajo este supuesto, las estimaciones de tales interacciones de alto orden son estimaciones de un cero exacto, por lo tanto, en realidad una estimación del error experimental.
Cuando hay muchos factores, serán necesarias muchas ejecuciones experimentales, incluso sin replicación. Por ejemplo, experimentar con 10 factores en dos niveles cada uno produce 2 10 = 1024 combinaciones. En algún momento esto se vuelve inviable debido al alto costo o a la falta de recursos. En este caso, se pueden utilizar diseños factoriales fraccionados .
Al igual que con cualquier experimento estadístico, las ejecuciones experimentales en un experimento factorial deben ser aleatorias para reducir el impacto que el sesgo podría tener en los resultados experimentales. En la práctica, esto puede representar un gran desafío operativo.
Los experimentos factoriales se pueden utilizar cuando hay más de dos niveles de cada factor. Sin embargo, el número de ejecuciones experimentales necesarias para diseños factoriales de tres niveles (o más) será considerablemente mayor que para sus contrapartes de dos niveles. Por lo tanto, los diseños factoriales son menos atractivos si un investigador desea considerar más de dos niveles.
Un experimento factorial se puede analizar utilizando ANOVA o análisis de regresión . [21] Para calcular el efecto principal de un factor "A" en un experimento de 2 niveles, reste la respuesta promedio de todas las ejecuciones experimentales para las cuales A estaba en su nivel bajo (o primer) de la respuesta promedio de todas las ejecuciones experimentales para las cuales A estaba en su nivel alto (o segundo).
Otras herramientas de análisis exploratorio útiles para experimentos factoriales incluyen gráficos de efectos principales , gráficos de interacción , gráficos de Pareto y un gráfico de probabilidad normal de los efectos estimados.
Cuando los factores son continuos, los diseños factoriales de dos niveles suponen que los efectos son lineales . Si se espera un efecto cuadrático para un factor, se debe utilizar un experimento más complicado, como un diseño compuesto central . La optimización de los factores que podrían tener efectos cuadráticos es el objetivo principal de la metodología de superficie de respuesta .
Montgomery [4] da el siguiente ejemplo de análisis de un experimento factorial:.
Un ingeniero desea aumentar la tasa de filtración (rendimiento) de un proceso para producir una sustancia química y reducir la cantidad de formaldehído utilizado en el proceso. Los intentos anteriores de reducir el formaldehído han reducido la tasa de filtración. La tasa de filtración actual es de 75 galones por hora. Se consideran cuatro factores: temperatura (A), presión (B), concentración de formaldehído (C) y velocidad de agitación (D). Cada uno de los cuatro factores se probará en dos niveles.
En adelante, los signos menos (−) y más (+) indicarán si el factor se ejecuta en un nivel bajo o alto, respectivamente.
Las líneas no paralelas en el gráfico de interacción A:C indican que el efecto del factor A depende del nivel del factor C. Un resultado similar se aplica a la interacción A:D. Los gráficos indican que el factor B tiene poco efecto en la tasa de filtración. El análisis de varianza (ANOVA) que incluye los 4 factores y todos los términos de interacción posibles entre ellos produce las estimaciones de coeficientes que se muestran en la siguiente tabla.
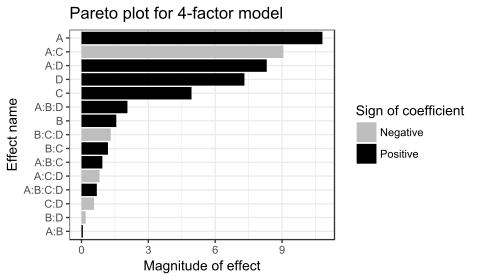
Dado que hay 16 observaciones y 16 coeficientes (intersección, efectos principales e interacciones), no se pueden calcular los valores p para este modelo. Los valores de los coeficientes y los gráficos sugieren que los factores importantes son A, C y D, y los términos de interacción A:C y A:D.
Los coeficientes de A, C y D son todos positivos en el ANOVA, lo que sugeriría ejecutar el proceso con las tres variables establecidas en el valor alto. Sin embargo, el efecto principal de cada variable es el promedio sobre los niveles de las otras variables. El gráfico de interacción A:C anterior muestra que el efecto del factor A depende del nivel del factor C, y viceversa. El factor A (temperatura) tiene muy poco efecto en la tasa de filtración cuando el factor C está en el nivel +. Pero el factor A tiene un gran efecto en la tasa de filtración cuando el factor C (formaldehído) está en el nivel -. La combinación de A en el nivel + y C en el nivel - da la tasa de filtración más alta. Esta observación indica cómo los análisis de un factor a la vez pueden pasar por alto interacciones importantes. Solo variando ambos factores A y C al mismo tiempo podría el ingeniero descubrir que el efecto del factor A depende del nivel del factor C.

La mejor tasa de filtración se observa cuando A y D están en el nivel alto y C está en el nivel bajo. Este resultado también satisface el objetivo de reducir el formaldehído (factor C). Como B no parece ser importante, se puede eliminar del modelo. Al realizar el ANOVA utilizando los factores A, C y D, y los términos de interacción A:C y A:D, se obtiene el resultado que se muestra en la siguiente tabla, en la que todos los términos son significativos (valor p < 0,05).