Función de compresión unidireccional

Primitivo criptográfico

En criptografía , una función de compresión unidireccional es una función que transforma dos entradas de longitud fija en una salida de longitud fija. ^[1] La transformación es "unidireccional" , lo que significa que es difícil, dada una salida particular, calcular entradas que se compriman a esa salida. Las funciones de compresión unidireccional no están relacionadas con los algoritmos de compresión de datos convencionales , que, en cambio, se pueden invertir de forma exacta (compresión sin pérdida) o aproximada (compresión con pérdida) a los datos originales.

Una función de compresión unidireccional

Las funciones de compresión unidireccional se utilizan, por ejemplo, en la construcción de Merkle-Damgård dentro de las funciones hash criptográficas .

Las funciones de compresión unidireccional suelen construirse a partir de cifrados de bloque . Algunos métodos para convertir cualquier cifrado de bloque normal en una función de compresión unidireccional son Davies–Meyer , Matyas–Meyer–Oseas , Miyaguchi–Preneel (funciones de compresión de longitud de bloque única) y MDC-2/Meyer–Schilling , MDC-4 , Hirose (funciones de compresión de longitud de bloque doble). Estos métodos se describen en detalle más adelante. ( MDC-2 es también el nombre de una función hash patentada por IBM ).

Otro método es 2BOW (o NBOW en general), que es una "función hash de alta velocidad y longitud de bloque múltiple basada en cifrados de bloque" ^[1] y que normalmente alcanza tasas (asintóticas) entre 1 y 2 independientemente del tamaño del hash (solo con una pequeña sobrecarga constante). Este método aún no ha sido analizado en términos de seguridad, por lo que debe manejarse con cuidado.

Compresión

Una función de compresión mezcla dos entradas de longitud fija y produce una única salida de longitud fija del mismo tamaño que una de las entradas. Esto también se puede ver como que la función de compresión transforma una entrada grande de longitud fija en una salida más corta de longitud fija.

Por ejemplo, la entrada A puede tener 128 bits, la entrada B 128 bits y se comprimen para formar una única salida de 128 bits. Esto equivale a tener una única entrada de 256 bits comprimida para formar una única salida de 128 bits.

Algunas funciones de compresión no comprimen a la mitad, sino por otro factor. Por ejemplo, la entrada A puede tener 256 bits y la entrada B 128 bits, que se comprimen en una única salida de 128 bits. Es decir, un total de 384 bits de entrada se comprimen en 128 bits de salida.

La mezcla se realiza de tal manera que se consigue un efecto de avalancha completo , es decir, cada bit de salida depende de cada bit de entrada.

De una sola mano

Una función unidireccional es una función que es fácil de calcular pero difícil de invertir. Una función de compresión unidireccional (también llamada función hash) debe tener las siguientes propiedades:

• Fácil de calcular: si tienes algunas entradas, es fácil calcular la salida.
• Resistencia a la preimagen: si un atacante solo conoce la salida, no debería ser factible calcular una entrada. En otras palabras, dada una salida , no debería ser factible calcular una entrada tal que . ${\displaystyle h}$ ${\displaystyle m}$ ${\displaystyle \operatorname {hash} (m)=h}$
• Segunda resistencia de preimagen: Dada una entrada cuya salida es , debería ser inviable encontrar otra entrada que tenga la misma salida , es decir . ${\displaystyle m_{1}}$ ${\displaystyle h}$ ${\displaystyle m_{2}}$ ${\displaystyle h}$ ${\displaystyle \operatorname {hash} (m_{1})=\operatorname {hash} (m_{2})}$
• Resistencia a colisiones: debería ser difícil encontrar dos entradas diferentes que se compriman en la misma salida, es decir, un atacante no debería poder encontrar un par de mensajes tales que . Debido a la paradoja del cumpleaños (ver también ataque de cumpleaños ) hay un 50% de posibilidades de que se pueda encontrar una colisión en un tiempo de aproximadamente donde es el número de bits en la salida de la función hash. Por lo tanto, un ataque a la función hash no debería poder encontrar una colisión con menos de aproximadamente trabajo. ${\displaystyle m_{1}\neq m_{2}}$ ${\displaystyle \operatorname {hash} (m_{1})=\operatorname {hash} (m_{2})}$ ${\displaystyle 2^{n/2}}$ ${\displaystyle n}$ ${\displaystyle 2^{n/2}}$

Lo ideal sería que la "inviabilidad" de la resistencia a la preimagen y de la segunda resistencia a la preimagen significara un trabajo de aproximadamente donde es el número de bits en la salida de la función hash. Sin embargo, particularmente para la resistencia a la segunda resistencia a la preimagen, este es un problema difícil. ^{[ cita requerida ]} ${\displaystyle 2^{n}}$ ${\displaystyle n}$

La construcción Merkle-Damgård

La construcción del hash Merkle–Damgård. Los cuadros etiquetados [f] son ​​una función de compresión unidireccional.

Un uso común de las funciones de compresión unidireccional es la construcción Merkle–Damgård dentro de las funciones hash criptográficas. Las funciones hash más utilizadas, incluidas MD5 , SHA-1 (que está en desuso ^[2] ) y SHA-2 , utilizan esta construcción.

Una función hash debe ser capaz de procesar un mensaje de longitud arbitraria y convertirlo en una salida de longitud fija. Esto se puede lograr dividiendo la entrada en una serie de bloques de igual tamaño y operando sobre ellos en secuencia utilizando una función de compresión unidireccional. La función de compresión puede estar especialmente diseñada para el hash o puede construirse a partir de un cifrado de bloques. El último bloque procesado también debe tener una longitud rellena , lo que es crucial para la seguridad de esta construcción.

Cuando se aplica el relleno de longitud (también llamado fortalecimiento de MD), los ataques no pueden encontrar colisiones más rápido que la paradoja del cumpleaños ( , siendo el tamaño del bloque en bits) si la función utilizada es resistente a colisiones. ^{[3] [4]} Por lo tanto, la construcción del hash de Merkle-Damgård reduce el problema de encontrar una función hash adecuada a encontrar una función de compresión adecuada. ${\displaystyle 2^{n/2}}$ ${\displaystyle n}$ ${\displaystyle f}$

Un segundo ataque de preimagen (dado un mensaje, un atacante encuentra otro mensaje para satisfacer) se puede realizar de acuerdo con Kelsey y Schneier ^[5] para un mensaje de bloque de mensajes en el tiempo . La complejidad de este ataque alcanza un mínimo de para mensajes largos cuando y se acerca cuando los mensajes son cortos. ${\displaystyle m_{1}}$ ${\displaystyle m_{2}}$ ${\displaystyle \operatorname {hash} (m_{1})=\operatorname {hash} (m_{2})}$ ${\displaystyle 2^{k}}$ ${\displaystyle k\times 2^{n/2+1}+2^{n-k+1}}$ ${\displaystyle 2^{3n/4+2}}$ ${\displaystyle k=2^{n/4}}$ ${\displaystyle 2^{n}}$

Construcción a partir de cifrados por bloques

Un cifrado de bloque moderno típico

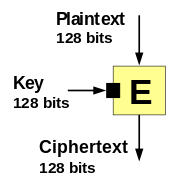
Las funciones de compresión unidireccional a menudo se construyen a partir de cifrados en bloque.

Los cifrados en bloque toman (como las funciones de compresión unidireccional) dos entradas de tamaño fijo (la clave y el texto simple ) y devuelven una única salida (el texto cifrado ) que es del mismo tamaño que el texto simple de entrada.

Sin embargo, los cifrados de bloques modernos son solo parcialmente unidireccionales. Es decir, dado un texto simple y un texto cifrado, no es factible encontrar una clave que encripte el texto simple con el texto cifrado. Pero, dado un texto cifrado y una clave, se puede encontrar un texto simple coincidente simplemente utilizando la función de descifrado del cifrador de bloques. Por lo tanto, para convertir un cifrado de bloques en una función de compresión unidireccional, se deben agregar algunas operaciones adicionales.

Algunos métodos para convertir cualquier cifrado de bloque normal en una función de compresión unidireccional son Davies–Meyer, Matyas–Meyer–Oseas, Miyaguchi–Preneel (funciones de compresión de longitud de bloque único) y MDC-2, MDC-4, Hirose (funciones de compresión de longitud de bloque doble).

Las funciones de compresión de longitud de un solo bloque generan la misma cantidad de bits que los procesados ​​por el cifrador de bloque subyacente. En consecuencia, las funciones de compresión de longitud de bloque doble generan el doble de bits.

Si un cifrador de bloques tiene un tamaño de bloque de, por ejemplo, 128 bits, los métodos de longitud de bloque único crean una función hash que tiene un tamaño de bloque de 128 bits y produce un hash de 128 bits. Los métodos de longitud de bloque doble crean hashes con el doble del tamaño de hash en comparación con el tamaño de bloque del cifrador de bloques utilizado. Por lo tanto, un cifrador de bloques de 128 bits se puede convertir en una función hash de 256 bits.

Estos métodos se utilizan luego dentro de la construcción de Merkle–Damgård para crear la función hash real. Estos métodos se describen en detalle más adelante.

El uso de un cifrador de bloques para construir la función de compresión unidireccional para una función hash suele ser algo más lento que el uso de una función de compresión unidireccional especialmente diseñada en la función hash. Esto se debe a que todas las construcciones seguras conocidas realizan la programación de claves para cada bloque del mensaje. Black, Cochran y Shrimpton han demostrado que es imposible construir una función de compresión unidireccional que realice una sola llamada a un cifrador de bloques con una clave fija. ^[6] En la práctica, se logran velocidades razonables siempre que la programación de claves del cifrador de bloques seleccionado no sea una operación demasiado pesada.

Pero, en algunos casos, es más fácil porque una única implementación de un cifrador de bloques se puede utilizar tanto para un cifrador de bloques como para una función hash. También puede ahorrar espacio de código en sistemas integrados muy pequeños, como por ejemplo tarjetas inteligentes o nodos en automóviles u otras máquinas.

Por lo tanto, la tasa de hash o tasa da una idea de la eficiencia de una función hash basada en una determinada función de compresión. La tasa de una función hash iterada describe la relación entre el número de operaciones de cifrado de bloque y la salida. Más precisamente, la tasa representa la relación entre el número de bits procesados ​​de entrada , la longitud de bits de salida del cifrado de bloque y las operaciones de cifrado de bloque necesarias para producir estos bits de salida. Generalmente, el uso de menos operaciones de cifrado de bloque da como resultado un mejor rendimiento general de toda la función hash, pero también conduce a un valor hash más pequeño, lo que podría ser indeseable. La tasa se expresa mediante la fórmula: ${\displaystyle m}$ ${\displaystyle n}$ ${\displaystyle s}$ ${\displaystyle n}$

${\displaystyle R_{h}={\frac {\left|m_{i}\right|}{s\cdot n}}}$

La función hash sólo puede considerarse segura si se cumplen al menos las siguientes condiciones:

• El cifrado por bloques no tiene propiedades especiales que lo distingan de los cifrados ideales, como claves débiles o claves que conducen a cifrados idénticos o relacionados (puntos fijos o colisiones de claves).
• El tamaño del hash resultante es lo suficientemente grande. Según el ataque de cumpleaños, es deseable un nivel de seguridad de 2,80 ⁽ que en general se considera inviable de calcular en la actualidad) ^{[ cita requerida ]} , por lo que el tamaño del hash debería ser de al menos 160 bits.
• El último bloque se rellena adecuadamente antes del hash. (Véase la construcción de Merkle–Damgård ). El relleno de longitud normalmente se implementa y se gestiona internamente en funciones hash especializadas como SHA-1 , etc.

Las construcciones presentadas a continuación: Davies–Meyer, Matyas–Meyer–Oseas, Miyaguchi–Preneel y Hirose han demostrado ser seguras bajo el análisis de caja negra . ^{[7] [8]} El objetivo es mostrar que cualquier ataque que se pueda encontrar es como máximo tan eficiente como el ataque de cumpleaños bajo ciertas suposiciones. El modelo de caja negra supone que se utiliza un cifrado de bloque que se elige aleatoriamente de un conjunto que contiene todos los cifrados de bloque apropiados. En este modelo, un atacante puede cifrar y descifrar libremente cualquier bloque, pero no tiene acceso a una implementación del cifrado de bloque. La función de cifrado y descifrado está representada por oráculos que reciben un par de un texto simple y una clave o un texto cifrado y una clave. Luego, los oráculos responden con un texto simple o cifrado elegido aleatoriamente, si el par se solicitó por primera vez. Ambos comparten una tabla para estos tripletes, un par de la consulta y la respuesta correspondiente, y devuelven el registro, si se recibió una consulta por segunda vez. Para demostrarlo, existe un algoritmo de búsqueda de colisiones que realiza consultas elegidas al azar a los oráculos. El algoritmo devuelve 1 si dos respuestas dan como resultado una colisión que involucra la función hash que se construye a partir de una función de compresión que aplica este cifrado de bloque (0 en caso contrario). La probabilidad de que el algoritmo devuelva 1 depende de la cantidad de consultas que determinan el nivel de seguridad.

Davies-Meyer

Función de compresión unidireccional de Davies-Meyer

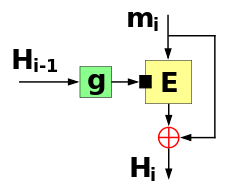
La función de compresión de longitud de bloque único de Davies-Meyer introduce cada bloque del mensaje ( ) como clave para un cifrado de bloque. Introduce el valor hash anterior ( ) como texto sin formato que se va a cifrar. El texto cifrado de salida también se combina con el valor hash anterior ( ) mediante XOR (⊕) para producir el siguiente valor hash ( ). En la primera ronda, cuando no hay ningún valor hash anterior, se utiliza un valor inicial constante preestablecido ( ). ${\displaystyle m_{i}}$ ${\displaystyle H_{i-1}}$ ${\displaystyle H_{i-1}}$ ${\displaystyle H_{i}}$ ${\displaystyle H_{0}}$

En notación matemática, Davies-Meyer se puede describir como:

${\displaystyle H_{i}=E_{m_{i}}{(H_{i-1})}\oplus {H_{i-1}}}$

El esquema tiene la tasa (k es el tamaño de la clave):

${\displaystyle R_{DM}={\frac {k}{1\cdot n}}={\frac {k}{n}}}$

Si el cifrado de bloques utiliza, por ejemplo, claves de 256 bits, entonces cada bloque de mensaje ( ) es un fragmento de 256 bits del mensaje. Si el mismo cifrado de bloques utiliza un tamaño de bloque de 128 bits, entonces los valores hash de entrada y salida en cada ronda son de 128 bits. ${\displaystyle m_{i}}$

Las variaciones de este método reemplazan XOR con cualquier otra operación de grupo, como la suma de enteros sin signo de 32 bits.

Una propiedad notable de la construcción de Davies-Meyer es que incluso si el cifrado de bloque subyacente es totalmente seguro, es posible calcular puntos fijos para la construcción: para cualquier , se puede encontrar un valor de tal que : uno solo tiene que establecer . ^[9] Esta es una propiedad que las funciones aleatorias ciertamente no tienen. Hasta ahora, ningún ataque práctico se ha basado en esta propiedad, pero uno debe ser consciente de esta "característica". Los puntos fijos se pueden usar en un segundo ataque de preimagen (dado un mensaje , el atacante encuentra otro mensaje para satisfacer ) de Kelsey y Schneier ^[5] para un mensaje de bloque de mensajes en el tiempo . Si la construcción no permite la creación fácil de puntos fijos (como Matyas–Meyer–Oseas o Miyaguchi–Preneel), entonces este ataque se puede hacer en el tiempo. En ambos casos, la complejidad es superior pero inferior cuando los mensajes son largos y cuando los mensajes se acortan la complejidad del ataque se acerca a . ${\displaystyle m}$ ${\displaystyle h}$ ${\displaystyle E_{m}(h)\oplus h=h}$ ${\displaystyle h=E_{m}^{-1}(0)}$ ${\displaystyle m_{1}}$ ${\displaystyle m_{2}}$ ${\displaystyle \operatorname {hash} (m_{1})=\operatorname {hash} (m_{2})}$ ${\displaystyle 2^{k}}$ ${\displaystyle 3\times 2^{n/2+1}+2^{n-k+1}}$ ${\displaystyle k\times 2^{n/2+1}+2^{n-k+1}}$ ${\displaystyle 2^{n/2}}$ ${\displaystyle 2^{n}}$ ${\displaystyle 2^{n}}$

La seguridad de la construcción de Davies-Meyer en el modelo de cifrado ideal fue demostrada por primera vez por R. Winternitz. ^[10]

Matías-Meyer-Oseas

Función de compresión unidireccional de Matyas-Meyer-Oseas

La función de compresión unidireccional de longitud de bloque único de Matyas–Meyer–Oseas puede considerarse el dual (el opuesto) de Davies–Meyer.

Se introduce cada bloque del mensaje ( ) como el texto simple que se va a cifrar. El texto cifrado de salida también se combina con el mismo bloque de mensaje ( ) para producir el siguiente valor hash ( ). El valor hash anterior ( ) se introduce como clave para el cifrado de bloque. En la primera ronda, cuando no hay ningún valor hash anterior, se utiliza un valor inicial constante preestablecido ( ). ${\displaystyle m_{i}}$ ${\displaystyle m_{i}}$ ${\displaystyle H_{i}}$ ${\displaystyle H_{i-1}}$ ${\displaystyle H_{0}}$

Si el cifrado de bloque tiene diferentes tamaños de bloque y de clave, el valor hash ( ) tendrá el tamaño incorrecto para usarse como clave. El cifrado también puede tener otros requisitos especiales para la clave. Luego, el valor hash se pasa primero a través de la función para convertirlo/rellenarlo para que se ajuste como clave para el cifrado. ${\displaystyle H_{i-1}}$ ${\displaystyle g}$

En notación matemática, Matyas–Meyer–Oseas se puede describir como:

${\displaystyle H_{i}=E_{g(H_{i-1})}(m_{i})\oplus m_{i}}$

El esquema tiene la tasa:

${\displaystyle R_{MMO}={\frac {n}{1\cdot n}}=1}$

Según Kelsey y Schneier ^[5], se puede realizar un segundo ataque de preimagen (dado un mensaje, un atacante encuentra otro mensaje para satisfacerlo ) para un mensaje de bloque de mensajes en el tiempo . La complejidad es mayor, pero menor cuando los mensajes son largos, y cuando los mensajes se acortan, la complejidad del ataque se acerca a . ${\displaystyle m_{1}}$ ${\displaystyle m_{2}}$ ${\displaystyle \operatorname {hash} (m_{1})=\operatorname {hash} (m_{2})}$ ${\displaystyle 2^{k}}$ ${\displaystyle k\times 2^{n/2+1}+2^{n-k+1}}$ ${\displaystyle 2^{n/2}}$ ${\displaystyle 2^{n}}$ ${\displaystyle 2^{n}}$

Miyaguchi–Preneel

La función de compresión unidireccional de Miyaguchi-Preneel

La función de compresión unidireccional de longitud de bloque único de Miyaguchi-Preneel es una variante extendida de Matyas-Meyer-Oseas. Fue propuesta independientemente por Shoji Miyaguchi y Bart Preneel .

Se introduce cada bloque del mensaje ( ) como el texto sin formato que se va a cifrar. A continuación, se realiza una operación XOR del texto cifrado de salida (⊕) con el mismo bloque de mensaje ( ) y, a continuación, también se realiza una operación XOR con el valor hash anterior ( ) para producir el siguiente valor hash ( ). El valor hash anterior ( ) se introduce como clave para el cifrado de bloque. En la primera ronda, cuando no hay ningún valor hash anterior, se utiliza un valor inicial constante preestablecido ( ). ${\displaystyle m_{i}}$ ${\displaystyle m_{i}}$ ${\displaystyle H_{i-1}}$ ${\displaystyle H_{i}}$ ${\displaystyle H_{i-1}}$ ${\displaystyle H_{0}}$

Si el cifrado de bloque tiene diferentes tamaños de bloque y de clave, el valor hash ( ) tendrá el tamaño incorrecto para usarse como clave. El cifrado también puede tener otros requisitos especiales para la clave. Luego, el valor hash se pasa primero a través de la función para convertirlo/rellenarlo para que se ajuste como clave para el cifrado. ${\displaystyle H_{i-1}}$ ${\displaystyle g}$

En notación matemática, Miyaguchi-Preneel se puede describir como:

${\displaystyle H_{i}=E_{g(H_{i-1})}(m_{i})\oplus H_{i-1}\oplus m_{i}}$

El esquema tiene la tasa:

${\displaystyle R_{MP}={\frac {n}{1\cdot n}}=1}$

Los roles de y pueden intercambiarse, de modo que se cifran con la clave , lo que convierte a este método en una extensión de Davies-Meyer. ${\displaystyle m_{i}}$ ${\displaystyle H_{i-1}}$ ${\displaystyle H_{i-1}}$ ${\displaystyle m_{i}}$

Según Kelsey y Schneier ^[5], se puede realizar un segundo ataque de preimagen (dado un mensaje, un atacante encuentra otro mensaje para satisfacerlo ) para un mensaje de bloque de mensajes en el tiempo . La complejidad es mayor, pero menor cuando los mensajes son largos, y cuando los mensajes se acortan, la complejidad del ataque se acerca a . ${\displaystyle m_{1}}$ ${\displaystyle m_{2}}$ ${\displaystyle \operatorname {hash} (m_{1})=\operatorname {hash} (m_{2})}$ ${\displaystyle 2^{k}}$ ${\displaystyle k\times 2^{n/2+1}+2^{n-k+1}}$ ${\displaystyle 2^{n/2}}$ ${\displaystyle 2^{n}}$ ${\displaystyle 2^{n}}$

Hirose

La función de compresión de longitud de bloque doble de Hirose

La función de compresión unidireccional de longitud de bloque doble de Hirose ^[8] consta de un cifrado de bloque más una permutación . Fue propuesta por Shoichi Hirose en 2006 y se basa en un trabajo ^[11] de Mridul Nandi. ${\displaystyle p}$

Utiliza un cifrado de bloque cuya longitud de clave es mayor que la longitud del bloque y produce un hash de tamaño . Por ejemplo, cualquiera de los candidatos AES con una clave de 192 o 256 bits (y un bloque de 128 bits). ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle 2n}$

Cada ronda acepta una parte del mensaje que tiene una longitud de bits y la utiliza para actualizar valores de estado de dos bits y . ${\displaystyle m_{i}}$ ${\displaystyle k-n}$ ${\displaystyle n}$ ${\displaystyle G}$ ${\displaystyle H}$

Primero, se concatena con para producir una clave . Luego, los dos valores de retroalimentación se actualizan de acuerdo con: ${\displaystyle m_{i}}$ ${\displaystyle H_{i-1}}$ ${\displaystyle K_{i}}$

• ${\displaystyle G_{i}=E_{K_{i}}(G_{i-1})\oplus G_{i-1}}$
• ${\displaystyle H_{i}=E_{K_{i}}(p(G_{i-1}))\oplus p(G_{i-1})}$

${\displaystyle p(G_{i-1})}$es una permutación arbitraria de punto fijo libre en un valor de bit, típicamente definida como para una constante arbitraria distinta de cero (todos unos pueden ser una opción conveniente). ${\displaystyle n}$ ${\displaystyle p(x)=x\oplus c}$ ${\displaystyle c}$

Cada cifrado se parece a la construcción estándar de Davies-Meyer. La ventaja de este esquema sobre otros esquemas propuestos de longitud de bloque doble es que ambos cifrados utilizan la misma clave y, por lo tanto, el esfuerzo de programación de claves puede compartirse.

El resultado final es . El esquema tiene la tasa relativa al cifrado del mensaje con el cifrado. ${\displaystyle H_{t}||G_{t}}$ ${\textstyle R_{Hirose}={\frac {k-n}{2n}}}$

Hirose también proporciona una prueba en el Modelo de Cifrado Ideal.

Construcción con esponja

La construcción de esponja se puede utilizar para construir funciones de compresión unidireccional.

Véase también

• Whirlpool : una función hash criptográfica creada utilizando la construcción Miyaguchi-Preneel y un cifrado de bloque similar a Square y AES .
• CBC-MAC , OMAC y PMAC : métodos para convertir cifrados de bloque en códigos de autenticación de mensajes (MAC).

Referencias

Citas

1. Manual de criptografía aplicada de Alfred J. Menezes, Paul C. van Oorschot y Scott A. Vanstone. Quinta edición (agosto de 2001), página 328.
2. "Anuncio de la primera colisión SHA1". Blog de seguridad en línea de Google . Consultado el 12 de enero de 2020 .
3. Ivan Damgård. Un principio de diseño para funciones hash. En Gilles Brassard, editor, CRYPTO, volumen 435 de LNCS, páginas 416–427. Springer, 1989.
4. Ralph Merkle. Funciones hash unidireccionales y DES. En Gilles Brassard, editor, CRYPTO, volumen 435 de LNCS, páginas 428–446. Springer, 1989.
5. John Kelsey y Bruce Schneier. Segundas preimágenes en funciones hash de n bits para un trabajo mucho menor que 2n. En Ronald Cramer, editor, EUROCRYPT, volumen 3494 de LNCS, páginas 474–490. Springer, 2005.
6. John Black, Martin Cochran y Thomas Shrimpton. On the Impossibility of Highly-Efficient Blockcipher-Based Hash Functions. Advances in Cryptology – EUROCRYPT '05, Aarhus, Dinamarca, 2005. Los autores definen una función hash como "altamente eficiente si su función de compresión utiliza exactamente una llamada a un cifrador de bloque cuya clave es fija".
7. John Black, Phillip Rogaway y Tom Shrimpton. Análisis de caja negra de las construcciones de funciones hash basadas en cifrado de bloques de PGV. Advances in Cryptology – CRYPTO '02, Lecture Notes in Computer Science, vol. 2442, págs. 320–335, Springer, 2002. Véase la tabla de la página 3. Davies–Meyer, Matyas–Meyer–Oseas y Miyaguchi–Preneel están numeradas en la primera columna como funciones hash 5, 1 y 3.
8. S. Hirose, Algunas construcciones plausibles de funciones hash de longitud de bloque doble . En: Robshaw, MJB (ed.) FSE 2006, LNCS, vol. 4047, págs. 210–225, Springer, Heidelberg 2006.
9. Manual de criptografía aplicada de Alfred J. Menezes, Paul C. van Oorschot y Scott A. Vanstone. Quinta edición (agosto de 2001), página 375.
10. R. Winternitz. Una función hash segura unidireccional construida a partir de DES. En Actas del Simposio IEEE sobre Seguridad de la Información y Privacidad, págs. 88-90. IEEE Press, 1984.
11. M. Nandi, Hacia funciones hash óptimas de doble longitud , en: Actas de la 6.ª Conferencia internacional sobre criptología en India (INDOCRYPT 2005), Lecture Notes in Computer Science 3797, páginas 77–89, 2005.

Fuentes

• Menezes; van Oorschot; Vanstone (2001). "Funciones hash e integridad de datos" (PDF) . Manual de criptografía aplicada.