Forma normal de Chomsky

Notación para gramáticas formales independientes del contexto

En la teoría del lenguaje formal , se dice que una gramática libre de contexto , G , está en la forma normal de Chomsky (descrita por primera vez por Noam Chomsky ) ^[1] si todas sus reglas de producción tienen la forma: ^{[2] [3]}

A → BC , o

A → a , o

S → ε,

donde A , B y C son símbolos no terminales , la letra a es un símbolo terminal (un símbolo que representa un valor constante), S es el símbolo de inicio y ε denota la cadena vacía . Además, ni B ni C pueden ser el símbolo de inicio , y la tercera regla de producción solo puede aparecer si ε está en L ( G ), el lenguaje producido por la gramática libre de contexto G . ^{[4] : 92–93, 106}

Toda gramática en forma normal de Chomsky es libre de contexto y, a la inversa, toda gramática libre de contexto puede transformarse en una equivalente [ ^{nota 1]} que esté en forma normal de Chomsky y tenga un tamaño no mayor que el cuadrado del tamaño de la gramática original.

Convertir una gramática a la forma normal de Chomsky

Para convertir una gramática a la forma normal de Chomsky, se aplica una secuencia de transformaciones simples en un cierto orden; esto se describe en la mayoría de los libros de texto sobre teoría de autómatas . ^{[4] : 87–94  [5] [6] [7]} La ​​presentación aquí sigue a Hopcroft, Ullman (1979), pero está adaptada para usar los nombres de transformación de Lange, Leiß (2009). ^{[8] [nota 2]} Cada una de las siguientes transformaciones establece una de las propiedades requeridas para la forma normal de Chomsky.

INICIO: Eliminar el símbolo de inicio de los lados derechos

Introduzca un nuevo símbolo de inicio S ₀ y una nueva regla

S0 → S ,_​

donde S es el símbolo de inicio anterior. Esto no cambia el idioma producido por la gramática y S ₀ no aparecerá en el lado derecho de ninguna regla.

TÉRMINO: Eliminar reglas con terminales no solitarias

Para eliminar cada regla

A → X ₁ ... a ... X _n

con un símbolo terminal a que no es el único símbolo en el lado derecho, introduzca, para cada terminal, un nuevo símbolo no terminal N _a , y una nueva regla

N _a → a .

Cambiar cada regla

A → X ₁ ... a ... X _n

a

A → X ₁ ... N _a ... X _n .

Si aparecen varios símbolos terminales en el lado derecho, reemplácelos simultáneamente por su símbolo no terminal asociado. Esto no modifica el lenguaje producido por la gramática. ^{[4] : 92}

BIN: Eliminar los lados derechos con más de 2 no terminales

Reemplazar cada regla

A → X ₁ X ₂ ... X _n

con más de 2 no terminales X ₁ ,..., X _n por reglas

A → X ₁ A ₁ ,

Un ₁ → X ₂ Un ₂ ,

... ,

A _{n -2} → X _{n -1} X _n ,

donde A _i son nuevos símbolos no terminales. Nuevamente, esto no cambia el lenguaje producido por la gramática. ^{[4] : 93}

DEL: Eliminar las reglas ε

Una regla ε es una regla de la forma

A → ε,

donde A no es S ₀ , el símbolo de inicio de la gramática.

Para eliminar todas las reglas de esta forma, primero se determina el conjunto de todos los no terminales que derivan ε. Hopcroft y Ullman (1979) llaman a estos no terminales nulos y los calculan de la siguiente manera:

• Si existe una regla A → ε, entonces A es nulo.
• Si existe una regla A → X ₁ ... X _n , y cada X _i es nulo, entonces A también es nulo.

Obtenga una gramática intermedia reemplazando cada regla

A → X ₁ ... X _n

en todas las versiones se omiten algunos valores nulos de X _i . Al eliminar en esta gramática cada regla ε, a menos que su lado izquierdo sea el símbolo de inicio, se obtiene la gramática transformada. ^{[4] : 90}

Por ejemplo, en la siguiente gramática, con símbolo de inicio S ₀ ,

S ₀ → AbB | C

B → AA | CA

C → b | c

A → a | ε

El no terminal A , y por lo tanto también B , es nulo, mientras que ni C ni S ₀ lo son. Por lo tanto, se obtiene la siguiente gramática intermedia: ^{[nota 3]}

S ₀ → AbB | AbB | AbB | AbB | AbB   |   C​​​​​​

B → AA | A A | A A | A ε A   |   A C | A C

C → b | c

A → a | ε

En esta gramática, todas las reglas ε se han " incorporado en línea en el sitio de la llamada". ^{[nota 4]} En el siguiente paso, se pueden eliminar, obteniendo la gramática:

S ₀ → AbB | Ab | bB | b   |   C

B → AA | A   |   CA | C

C → b | c

Un → un

Esta gramática produce el mismo lenguaje que la gramática de ejemplo original, a saber. { ab , aba , abaa , abab , abac , abb , abc , b , ba , baa , bab , bac , bb , bc , c }, pero no tiene reglas ε.

UNIDAD: Eliminar reglas de unidad

Una regla de unidad es una regla de la forma

A → B ,

donde A , B son símbolos no terminales. Para eliminarlo, para cada regla

B → X ₁ ... X _n ,

donde X ₁ ... X _n es una cadena de no terminales y terminales, agregue la regla

A → X ₁ ... X _n

a menos que se trate de una regla de unidad que ya se ha eliminado (o se está eliminando). La omisión del símbolo no terminal B en la gramática resultante es posible debido a que B es un miembro del cierre de unidad del símbolo no terminal A. [ ^9]

Orden de transformaciones

Al elegir el orden en el que se aplicarán las transformaciones anteriores, se debe tener en cuenta que algunas transformaciones pueden destruir el resultado obtenido por otras. Por ejemplo, START reintroducirá una regla de unidad si se aplica después de UNIT . La tabla muestra qué ordenaciones se admiten.

Además, el aumento en el tamaño de la gramática en el peor de los casos ^{[nota 5]} depende del orden de transformación. Usando | G | para denotar el tamaño de la gramática original G , el aumento de tamaño en el peor de los casos puede variar de | G | ² a 2 ^{2 |G|} , dependiendo del algoritmo de transformación usado. ^{[8] : 7} El aumento en el tamaño de la gramática depende del orden entre DEL y BIN . Puede ser exponencial cuando DEL se hace primero, pero es lineal en caso contrario. UNIT puede incurrir en un aumento cuadrático en el tamaño de la gramática. ^{[8] : 5} Los ordenamientos START , TERM , BIN , DEL , UNIT y START , BIN , DEL , UNIT , TERM conducen al menor aumento (es decir, cuadrático).

Ejemplo

Árbol sintáctico abstracto de la expresión aritmética " a ^2+4* b " con respecto a la gramática de ejemplo ( arriba ) y su forma normal de Chomsky ( abajo )

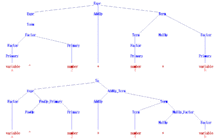
La siguiente gramática, cuyo símbolo inicial es Expr , describe una versión simplificada del conjunto de todas las expresiones aritméticas sintácticas válidas en lenguajes de programación como C o Algol60 . Tanto el número como la variable se consideran símbolos terminales aquí para simplificar, ya que en la interfaz de un compilador, el analizador no suele tener en cuenta su estructura interna . El símbolo terminal "^" denota exponenciación en Algol60.

En el paso "INICIO" del algoritmo de conversión anterior, solo se agrega una regla S ₀ → Expr a la gramática. Después del paso "TERM", la gramática se ve así:

Después del paso "BIN", se obtiene la siguiente gramática:

Como no existen reglas ε, el paso "DEL" no modifica la gramática. Después del paso "UNIT", se obtiene la siguiente gramática, que está en la forma normal de Chomsky:

Las N _a introducidas en el paso "TERM" son PowOp , Open y Close . Las A _i introducidas en el paso "BIN" son AddOp_Term , MulOp_Factor , PowOp_Primary y Expr_Close .

Definición alternativa

Forma reducida de Chomsky

Otra forma ^{[4] : 92  [10]} de definir la forma normal de Chomsky es:

Una gramática formal está en la forma reducida de Chomsky si todas sus reglas de producción son de la forma:

${\displaystyle A\rightarrow \,BC}$o

${\displaystyle A\rightarrow \,a}$,

donde , y son símbolos no terminales, y es un símbolo terminal . Al utilizar esta definición, o puede ser el símbolo de inicio. Solo aquellas gramáticas libres de contexto que no generan la cadena vacía pueden transformarse en la forma reducida de Chomsky. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle a}$ ${\displaystyle B}$ ${\displaystyle C}$

Forma normal de Floyd

En una carta en la que propuso un término forma Backus–Naur (BNF), Donald E. Knuth dio a entender una "sintaxis BNF en la que todas las definiciones tienen una forma tal que se puede decir que están en 'forma normal de Floyd'",

${\displaystyle \langle A\rangle ::=\,\langle B\rangle \mid \langle C\rangle }$o

${\displaystyle \langle A\rangle ::=\,\langle B\rangle \langle C\rangle }$o

${\displaystyle \langle A\rangle ::=\,a}$,

donde , y son símbolos no terminales, y es un símbolo terminal, porque Robert W. Floyd encontró que cualquier sintaxis BNF puede convertirse a la anterior en 1961. ^[11] Pero retiró este término, "ya que sin duda muchas personas han usado independientemente este simple hecho en su propio trabajo, y el punto es solo incidental a las consideraciones principales de la nota de Floyd". ^[12] Mientras que la nota de Floyd cita el artículo original de Chomsky de 1959, la carta de Knuth no lo hace. ${\displaystyle \langle A\rangle }$ ${\displaystyle \langle B\rangle }$ ${\displaystyle \langle C\rangle }$ ${\displaystyle a}$

Solicitud

Además de su importancia teórica, la conversión CNF se utiliza en algunos algoritmos como un paso de preprocesamiento, por ejemplo, el algoritmo CYK , un análisis de abajo hacia arriba para gramáticas libres de contexto, y su variante probabilística CKY. ^[13]

Véase también

• Forma Backus-Naur
• Algoritmo CYK
• Forma normal de Greibach
• Forma normal de Kuroda
• Lema de bombeo para lenguajes libres de contexto : su prueba se basa en la forma normal de Chomsky

Notas

1. es decir, uno que produce el mismo lenguaje
2. Por ejemplo, Hopcroft, Ullman (1979) fusionó TERM y BIN en una sola transformación.
3. N no terminal mantenida y omitida por N y N , respectivamente
4. Si la gramática tenía una regla S ₀ → ε, no se podía "incorporar" porque no tenía "sitios de llamada". Por lo tanto, no se podía eliminar en el siguiente paso.
5. es decir longitud escrita, medida en símbolos

Referencias

1. Chomsky, Noam (1959). "Sobre ciertas propiedades formales de las gramáticas". Información y control . 2 (2): 137–167. doi :10.1016/S0019-9958(59)90362-6.Aquí: Sect.6, p.152ff.
2. D'Antoni, Loris. "Página 7, lección 9: Algoritmos de análisis de abajo hacia arriba" (PDF) . CS536-S21 Introducción a los lenguajes de programación y compiladores . Universidad de Wisconsin-Madison. Archivado (PDF) desde el original el 19 de julio de 2021.
3. Sipser, Michael (2006). Introducción a la teoría de la computación (2.ª ed.). Boston: Thomson Course Technology. Definición 2.8. ISBN 0-534-95097-3.OCLC 58544333  .
4. Hopcroft, John E.; Ullman, Jeffrey D. (1979). Introducción a la teoría de autómatas, lenguajes y computación. Reading, Massachusetts: Addison-Wesley Publishing. ISBN 978-0-201-02988-8.
5. Hopcroft, John E.; Motwani, Rajeev; Ullman, Jeffrey D. (2006). Introducción a la teoría de autómatas, lenguajes y computación (3.ª ed.). Addison-Wesley. ISBN 978-0-321-45536-9.Sección 7.1.5, pág. 272
6. Rich, Elaine (2007). "11.8 Formas normales". Autómatas, computabilidad y complejidad: teoría y aplicaciones (PDF) (1.ª ed.). Prentice-Hall. pág. 169. ISBN 978-0132288064. Archivado desde el original (PDF) el 17 de enero de 2023.
7. Wegener, Ingo (1993). Theoretische Informatik: un algoritmo orientado a la configuración . Leitfäden und Mongraphien der Informatik (en alemán). Stuttgart: BG Teubner. ISBN 978-3-519-02123-0.Sección 6.2 "Die Chomsky-Normalform für kontextfreie Grammatiken", p. 149-152
8. Lange, Martin; Leiß, Hans (2009). "¿CNF o no CNF? Una versión eficiente y presentable del algoritmo CYK" (PDF) . Informatica Didactica . 8 . Archivado (PDF) desde el original el 19 de julio de 2011.
9. Allison, Charles D. (2022). Fundamentos de la informática: una introducción accesible a los autómatas y los lenguajes formales . Fresh Sources, Inc. pág. 176. ISBN 9780578944173.
10. Hopcroft et al. (2006) ^{[ página necesaria ]}
11. Floyd, Robert W. (1961). "Nota sobre inducción matemática en gramáticas de estructura sintagmática" (PDF) . Información y Control . 4 (4): 353–358. doi : 10.1016/S0019-9958(61)80052-1 . Archivado (PDF) desde el original el 2021-03-05.Aquí: p.354
12. Knuth, Donald E. (diciembre de 1964). "Forma normal de Backus frente a forma de Backus Naur". Comunicaciones de la ACM . 7 (12): 735–736. doi : 10.1145/355588.365140 . S2CID  47537431.
13. Jurafsky, Daniel; Martin, James H. (2008). Procesamiento del habla y del lenguaje (2.ª ed.). Pearson Prentice Hall. pág. 465. ISBN 978-0-13-187321-6.

Lectura adicional

• Cole, Richard. Conversión de CFG a CNF (forma normal de Chomsky) , 17 de octubre de 2007. (pdf) — utiliza el orden TERM, BIN, START, DEL, UNIT.
• John Martin (2003). Introducción a los lenguajes y la teoría de la computación . McGraw Hill. ISBN 978-0-07-232200-2. (Páginas 237–240 de la sección 6.6: formas simplificadas y formas normales).
• Michael Sipser (1997). Introducción a la teoría de la computación. PWS Publishing. ISBN 978-0-534-94728-6. (Páginas 98–101 de la sección 2.1: gramáticas libres de contexto. Página 156.)
• Charles D. Allison (2021) (20 de agosto de 2021). Fundamentos de la informática: una introducción accesible al lenguaje formal . Fresh Sources, Inc. ISBN 9780578944173.{{cite book}}: CS1 maint: nombres numéricos: lista de autores ( enlace ) (páginas 171-183 de la sección 7.1: Forma normal de Chomsky)
• Sipser, Michael. Introducción a la teoría de la computación, 2.ª edición.
• Alexander Meduna (6 de diciembre de 2012). Autómatas y lenguajes: teoría y aplicaciones. Springer Science & Business Media. ISBN 978-1-4471-0501-5.