En matemáticas , particularmente en sistemas dinámicos , un diagrama de bifurcación muestra los valores visitados o aproximados asintóticamente (puntos fijos, órbitas periódicas o atractores caóticos ) de un sistema en función de un parámetro de bifurcación en el sistema. [ cita requerida ] Es habitual representar los valores estables con una línea continua y los inestables con una línea de puntos, aunque a menudo se omiten los puntos inestables. Los diagramas de bifurcación permiten la visualización de la teoría de bifurcación . En el contexto de los sistemas dinámicos de tiempo discreto, el diagrama también se denomina diagrama de órbita .


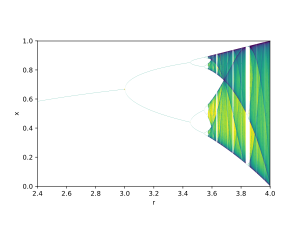
Un ejemplo es el diagrama de bifurcación del mapa logístico :
El parámetro de bifurcación r se muestra en el eje horizontal del gráfico y el eje vertical muestra el conjunto de valores de la función logística visitada asintóticamente desde casi todas las condiciones iniciales.
El diagrama de bifurcación muestra la bifurcación de los períodos de las órbitas estables de 1 a 2 a 4 a 8, etc. Cada uno de estos puntos de bifurcación es una bifurcación de duplicación de período . La relación de las longitudes de los intervalos sucesivos entre los valores de r para los que se produce la bifurcación converge a la primera constante de Feigenbaum .
El diagrama también muestra duplicaciones de períodos de 3 a 6, a 12, etc., de 5 a 10, a 20, etc., y así sucesivamente.

En un sistema dinámico como el que es estructuralmente estable cuando , si se traza un diagrama de bifurcación, considerando como el parámetro de bifurcación, pero para diferentes valores de , el caso es la bifurcación en horquilla simétrica. Cuando , decimos que tenemos una horquilla con simetría rota. Esto se ilustra en la animación de la derecha.
Consideremos un sistema de ecuaciones diferenciales que describe alguna cantidad física, que para ser más concretos podría representar uno de tres ejemplos: 1. la posición y velocidad de un péndulo sin fricción y sin amortiguamiento, 2. el potencial de membrana de una neurona a lo largo del tiempo, y 3. la concentración promedio de un virus en el torrente sanguíneo de un paciente. Las ecuaciones diferenciales para estos ejemplos incluyen *parámetros* que pueden afectar el resultado de las ecuaciones. Cambiar la masa y la longitud del péndulo afectará su frecuencia de oscilación, cambiar la magnitud de la corriente inyectada en una neurona puede hacer que el potencial de membrana pase de reposo a picos, y la carga viral a largo plazo en el torrente sanguíneo puede disminuir con tratamientos cuidadosamente programados.
En general, los investigadores pueden intentar cuantificar cómo cambia el comportamiento a largo plazo (asintótico) de un sistema de ecuaciones diferenciales si se modifica un parámetro. En la rama de los sistemas dinámicos de las matemáticas, un diagrama de bifurcación cuantifica estos cambios mostrando cómo cambian los puntos fijos, las órbitas periódicas o los atractores caóticos de un sistema en función del parámetro de bifurcación . Los diagramas de bifurcación se utilizan para visualizar estos cambios.