Estimación del espaciado máximo

Método de estimación de los parámetros de un modelo estadístico

El método de espaciado máximo intenta encontrar una función de distribución tal que los espaciamientos, D _{( i )} , tengan aproximadamente la misma longitud. Esto se hace maximizando su media geométrica .

En estadística , la estimación del espaciado máximo ( MSE o MSP ), o estimación del producto máximo del espaciado (MPS) , es un método para estimar los parámetros de un modelo estadístico univariado . ^[1] El método requiere la maximización de la media geométrica de los espaciamientos en los datos, que son las diferencias entre los valores de la función de distribución acumulativa en puntos de datos vecinos.

El concepto subyacente al método se basa en la transformada integral de probabilidad , en la que un conjunto de muestras aleatorias independientes derivadas de cualquier variable aleatoria debería, en promedio, estar distribuidas uniformemente con respecto a la función de distribución acumulativa de la variable aleatoria. El método MPS elige los valores de los parámetros que hacen que los datos observados sean lo más uniformes posible, de acuerdo con una medida cuantitativa específica de uniformidad.

Uno de los métodos más comunes para estimar los parámetros de una distribución a partir de datos, el método de máxima verosimilitud (MLE), puede fallar en varios casos, como cuando se trata de ciertas mezclas de distribuciones continuas. ^[2] En estos casos, el método de estimación de espaciamiento máximo puede resultar exitoso.

Además de su uso en matemáticas puras y estadística, se han reportado aplicaciones de prueba del método utilizando datos de campos como hidrología , ^[3] econometría , ^[4] imágenes por resonancia magnética , ^[5] y otros. ^[6]

Historia y uso

El método MSE fue derivado independientemente por Russel Cheng y Nik Amin en el Instituto de Ciencia y Tecnología de la Universidad de Gales , y Bo Ranneby en la Universidad Sueca de Ciencias Agrícolas . ^[2] Los autores explicaron que debido a la transformación integral de probabilidad en el parámetro verdadero, el "espaciamiento" entre cada observación debería distribuirse uniformemente. Esto implicaría que la diferencia entre los valores de la función de distribución acumulativa en observaciones consecutivas debería ser igual. Este es el caso que maximiza la media geométrica de tales espaciamientos, por lo que resolver los parámetros que maximizan la media geométrica lograría el "mejor" ajuste según se define de esta manera. Ranneby (1984) justificó el método demostrando que es un estimador de la divergencia de Kullback-Leibler , similar a la estimación de máxima verosimilitud , pero con propiedades más robustas para algunas clases de problemas.

Existen ciertas distribuciones, especialmente aquellas con tres o más parámetros, cuyas probabilidades pueden volverse infinitas a lo largo de ciertas trayectorias en el espacio de parámetros . El uso de la máxima verosimilitud para estimar estos parámetros a menudo falla, ya que un parámetro tiende al valor específico que hace que la probabilidad sea infinita, lo que hace que los otros parámetros sean inconsistentes. Sin embargo, el método de espaciamiento máximo, al depender de la diferencia entre los puntos de la función de distribución acumulativa y no de los puntos de probabilidad individuales, no tiene este problema y arrojará resultados válidos en una gama mucho más amplia de distribuciones. ^[1]

Las distribuciones que tienden a presentar problemas de verosimilitud son a menudo las que se utilizan para modelar fenómenos físicos. Hall y otros (2004) tratan de analizar métodos de mitigación de inundaciones, lo que requiere modelos precisos de los efectos de las inundaciones fluviales. Las distribuciones que mejor modelan estos efectos son todas modelos de tres parámetros, que sufren el problema de la verosimilitud infinita descrita anteriormente, lo que llevó a Hall a investigar el procedimiento de espaciamiento máximo. Wong y Li (2006), al comparar el método con la verosimilitud máxima, utilizan varios conjuntos de datos que van desde un conjunto sobre las edades más avanzadas al morir en Suecia entre 1905 y 1958 hasta un conjunto que contiene las velocidades máximas anuales del viento.

Definición

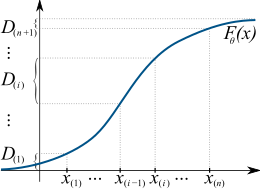
Dada una muestra aleatoria iid { x ₁ , ..., x _n } de tamaño n de una distribución univariante con función de distribución acumulativa continua F ( x ; θ ₀ ), donde θ ₀ ∈ Θ es un parámetro desconocido a estimar , sea { x ₍₁₎ , ..., x _{( n ) } la muestra} ordenada correspondiente , que es el resultado de ordenar todas las observaciones de menor a mayor. Para mayor comodidad, denotemos también x ₍₀₎ = −∞ y x _{( n +1)} = +∞.

Defina los espaciamientos como los “espacios” entre los valores de la función de distribución en puntos ordenados adyacentes: ^[7] $${\displaystyle D_{i}(\theta )=F(x_{(i)};\,\theta )-F(x_{(i-1)};\,\theta ),\quad i=1,\ldots ,n+1.}$$

Entonces, el estimador de espaciamiento máximo de θ ₀ se define como un valor que maximiza el logaritmo de la media geométrica de los espaciamientos muestrales: $${\displaystyle {\hat {\theta }}={\underset {\theta \in \Theta }{\operatorname {arg\,max} }}\;S_{n}(\theta ),\quad {\text{where }}\ S_{n}(\theta )=\ln \!\!{\sqrt[{n+1}]{D_{1}D_{2}\cdots D_{n+1}}}={\frac {1}{n+1}}\sum _{i=1}^{n+1}\ln {D_{i}}(\theta ).}$$

Por la desigualdad de las medias aritméticas y geométricas , la función S _n ( θ ) está acotada superiormente por −ln( n +1), y por tanto el máximo tiene que existir al menos en sentido supremo .

Obsérvese que algunos autores definen la función S _n ( θ ) de forma algo diferente. En particular, Ranneby (1984) multiplica cada D _i por un factor de ( n +1), mientras que Cheng & Stephens (1989) omiten el factor 1 ⁄ n +1 delante de la suma y añaden el signo “−” para convertir la maximización en minimización. Como se trata de constantes con respecto a θ , las modificaciones no alteran la ubicación del máximo de la función S _n .

Ejemplos

En esta sección se presentan dos ejemplos de cálculo del estimador de espaciado máximo.

Ejemplo 1

Gráficos del valor logarítmico de λ para el ejemplo simplista, tanto en el caso de la estimación de verosimilitud como del espaciamiento. Se identifican los valores para los que se maximizan tanto la verosimilitud como el espaciamiento, es decir, las estimaciones de verosimilitud máxima y espaciamiento máximo.

Supongamos que se tomaron dos valores x ₍₁₎ = 2, x _{(2) = 4 de la} distribución exponencial F ( x ; λ ) = 1 − e ^{− xλ} , x ≥ 0 con parámetro desconocido λ > 0. Para construir el MSE primero tenemos que encontrar los espaciamientos:

El proceso continúa encontrando el λ que maximiza la media geométrica de la columna de “diferencia”. Usando la convención que ignora tomar la raíz ( n + 1)a, esto se convierte en la maximización del siguiente producto: (1 − e ^{−2 λ} ) · (e ^{−2 λ} − e ^{−4 λ} ) · (e ^{−4 λ} ). Dejando μ = e ^{−2 λ} , el problema se convierte en encontrar el máximo de μ ⁵ −2 μ ⁴ + μ ³ . Derivando, el μ tiene que satisfacer 5 μ ⁴ −8 μ ³ +3 μ ² = 0. Esta ecuación tiene raíces 0, 0.6 y 1. Como μ es en realidad e ^{−2 λ} , tiene que ser mayor que cero pero menor que uno. Por lo tanto, la única solución aceptable es la que corresponde a una distribución exponencial con una media de 1 ⁄ λ ≈ 3,915. A modo de comparación, la estimación de máxima verosimilitud de λ es la inversa de la media de la muestra, 3, por lo que λ _MLE = ⅓ ≈ 0,333. $${\displaystyle \mu =0.6\quad \Rightarrow \quad \lambda _{\text{MSE}}={\frac {\ln 0.6}{-2}}\approx 0.255,}$$

Ejemplo 2

Supongamos que { x ₍₁₎ , ..., x _{( n )} } es la muestra ordenada de una distribución uniforme U ( a , b ) con extremos desconocidos a y b . La función de distribución acumulativa es F ( x ; a , b ) = ( x − a )/( b − a ) cuando x ∈[ a , b ]. Por lo tanto, los espaciamientos individuales se dan por $${\displaystyle D_{1}={\frac {x_{(1)}-a}{b-a}},\ \ D_{i}={\frac {x_{(i)}-x_{(i-1)}}{b-a}}\ {\text{for }}i=2,\ldots ,n,\ \ D_{n+1}={\frac {b-x_{(n)}}{b-a}}\ \ }$$

Calculando la media geométrica y luego sacando el logaritmo, el estadístico S _n será igual a Aquí sólo tres términos dependen de los parámetros a y b . Derivando con respecto a esos parámetros y resolviendo el sistema lineal resultante, las estimaciones de espaciado máximo serán $${\displaystyle S_{n}(a,b)={\tfrac {\ln(x_{(1)}-a)}{n+1}}+{\tfrac {\sum _{i=2}^{n}\ln(x_{(i)}-x_{(i-1)})}{n+1}}+{\tfrac {\ln(b-x_{(n)})}{n+1}}-\ln(b-a)}$$

${\displaystyle {\hat {a}}={\frac {nx_{(1)}-x_{(n)}}{n-1}},\ \ {\hat {b}}={\frac {nx_{(n)}-x_{(1)}}{n-1}}.}$

Se sabe que estos son los estimadores insesgados de varianza mínima uniforme (UMVU) para la distribución uniforme continua. ^[1] En comparación, las estimaciones de máxima verosimilitud para este problema son sesgadas y tienen un error cuadrático medio más alto . ${\displaystyle \scriptstyle {\hat {a}}=x_{(1)}}$ ${\displaystyle \scriptstyle {\hat {b}}=x_{(n)}}$

Propiedades

Coherencia y eficiencia

Gráfico de una función de densidad en forma de J y su distribución correspondiente. Una función Weibull desplazada con un parámetro de escala de 15, un parámetro de forma de 0,5 y un parámetro de ubicación de 10. La densidad se acerca asintóticamente al infinito a medida que x se acerca a 10, lo que hace que las estimaciones de los demás parámetros sean inconsistentes. Nótese que no hay un punto de inflexión en el gráfico de la distribución.

El estimador de espaciado máximo es un estimador consistente en el sentido de que converge en probabilidad al valor verdadero del parámetro, θ ₀ , a medida que el tamaño de la muestra aumenta hasta el infinito. ^[2] La consistencia de la estimación de espaciado máximo se mantiene en condiciones mucho más generales que para los estimadores de máxima verosimilitud . En particular, en los casos en que la distribución subyacente tiene forma de J, la máxima verosimilitud fallará donde MSE tiene éxito. ^[1] Un ejemplo de una densidad en forma de J es la distribución Weibull , específicamente una Weibull desplazada , con un parámetro de forma menor que 1. La densidad tenderá al infinito a medida que x se aproxima al parámetro de ubicación, lo que hace que las estimaciones de los otros parámetros sean inconsistentes.

Los estimadores de espaciamiento máximo también son al menos tan eficientes asintóticamente como los estimadores de máxima verosimilitud, cuando estos últimos existen. Sin embargo, pueden existir MSE en casos en que no existan MLE. ^[1]

Sensibilidad

Los estimadores de espaciado máximo son sensibles a observaciones muy espaciadas, y especialmente a los empates. ^[8] Dado que obtenemos $${\displaystyle X_{i+k}=X_{i+k-1}=\cdots =X_{i},\,}$$ $${\displaystyle D_{i+k}(\theta )=D_{i+k-1}(\theta )=\cdots =D_{i+1}(\theta )=0.\,}$$

Cuando los empates se deben a observaciones múltiples, los espaciamientos repetidos (aquellos que de otro modo serían cero) deben reemplazarse por la probabilidad correspondiente. ^[1] Es decir, se debe sustituir por , ya que . ${\displaystyle f_{i}(\theta )}$ ${\displaystyle D_{i}(\theta )}$ $${\displaystyle \lim _{x_{i}\to x_{i-1}}{\frac {\int _{x_{i-1}}^{x_{i}}f(t;\theta )\,dt}{x_{i}-x_{i-1}}}=f(x_{i-1},\theta )=f(x_{i},\theta ),}$$ ${\displaystyle x_{i}=x_{i-1}}$

Cuando los empates se deben a un error de redondeo, Cheng y Stephens (1989) sugieren otro método para eliminar los efectos. ^{[nota 1]} Dadas r observaciones empatadas de x _i a x _{i + r −1} , sea δ el error de redondeo . Todos los valores verdaderos deberían caer entonces en el rango . Los puntos correspondientes en la distribución deberían caer ahora entre y . Cheng y Stephens sugieren suponer que los valores redondeados están espaciados uniformemente en este intervalo, definiendo ${\displaystyle x\pm \delta }$ ${\displaystyle y_{L}=F(x-\delta ,{\hat {\theta }})}$ ${\displaystyle y_{U}=F(x+\delta ,{\hat {\theta }})}$ $${\displaystyle D_{j}={\frac {y_{U}-y_{L}}{r-1}}\quad (j=i+1,\ldots ,i+r-1).}$$

El método MSE también es sensible al agrupamiento secundario. ^[8] Un ejemplo de este fenómeno es cuando se piensa que un conjunto de observaciones proviene de una única distribución normal , pero en realidad proviene de una mezcla de normales con diferentes medias. Un segundo ejemplo es cuando se piensa que los datos provienen de una distribución exponencial , pero en realidad provienen de una distribución gamma . En el último caso, pueden ocurrir espaciamientos más pequeños en la cola inferior. Un valor alto de M ( θ ) indicaría este efecto de agrupamiento secundario y sugeriría que se requiere una mirada más cercana a los datos. ^[8]

Prueba de Moran

La estadística S _n ( θ ) es también una forma de la estadística de Moran o Moran-Darling, M ( θ ), que se puede utilizar para probar la bondad de ajuste . ^{[nota 2]} Se ha demostrado que la estadística, cuando se define como es asintóticamente normal , y que existe una aproximación de chi-cuadrado para muestras pequeñas. ^[8] En el caso en el que conocemos el parámetro verdadero , Cheng y Stephens (1989) muestran que la estadística tiene una distribución normal con donde γ es la constante de Euler-Mascheroni que es aproximadamente 0,57722. ^{[nota 3]} $${\displaystyle S_{n}(\theta )=M_{n}(\theta )=-\sum _{j=1}^{n+1}\ln {D_{j}(\theta )},}$$ ${\displaystyle \theta ^{0}}$ ${\displaystyle \scriptstyle M_{n}(\theta )}$ $${\displaystyle {\begin{aligned}\mu _{M}&\approx (n+1)(\ln(n+1)+\gamma )-{\frac {1}{2}}-{\frac {1}{12(n+1)}},\\\sigma _{M}^{2}&\approx (n+1)\left({\frac {\pi ^{2}}{6}}-1\right)-{\frac {1}{2}}-{\frac {1}{6(n+1)}},\end{aligned}}}$$

La distribución también puede aproximarse mediante la de , donde , en la que y donde sigue una distribución de chi-cuadrado con grados de libertad . Por lo tanto, para probar la hipótesis de que una muestra aleatoria de valores proviene de la distribución , se puede calcular el estadístico . Luego debe rechazarse con significancia si el valor es mayor que el valor crítico de la distribución de chi-cuadrado apropiada. ^[8] ${\displaystyle A}$ $${\displaystyle A=C_{1}+C_{2}\chi _{n}^{2}\,}$$ $${\displaystyle {\begin{aligned}C_{1}&=\mu _{M}-{\sqrt {\frac {\sigma _{M}^{2}n}{2}}},\\C_{2}&={\sqrt {\frac {\sigma _{M}^{2}}{2n}}},\\\end{aligned}}}$$ ${\displaystyle \chi _{n}^{2}}$ ${\displaystyle n}$ ${\displaystyle H_{0}}$ ${\displaystyle n}$ ${\displaystyle F(x,\theta )}$ ${\displaystyle T(\theta )={\frac {M(\theta )-C_{1}}{C_{2}}}}$ ${\displaystyle H_{0}}$ ${\displaystyle \alpha }$

Cheng y Stephens (1989) demostraron que, donde θ ₀ se estima mediante la misma media y varianza asintóticas que en el caso conocido, sin embargo, la estadística de prueba que se utilizará requiere la adición de un término de corrección de sesgo y es: donde es el número de parámetros en la estimación. ${\displaystyle {\hat {\theta }}}$ ${\displaystyle S_{n}({\hat {\theta }})=M_{n}({\hat {\theta }})}$ $${\displaystyle T({\hat {\theta }})={\frac {M({\hat {\theta }})+{\frac {k}{2}}-C_{1}}{C_{2}}},}$$ ${\displaystyle k}$

Espaciamiento máximo generalizado

Medidas y espaciamientos alternativos

Ranneby y Ekström (1997) generalizaron el método MSE para aproximar otras medidas además de la medida de Kullback-Leibler. Ekström (1997) expandió aún más el método para investigar las propiedades de los estimadores utilizando espaciamientos de orden superior, donde un espaciamiento de orden m se definiría como . ${\displaystyle F(X_{j+m})-F(X_{j})}$

Distribuciones multivariadas

Ranneby y otros (2005) analizan métodos de espaciado máximo extendidos para el caso multivariado . Como no existe un orden natural para , analizan dos enfoques alternativos: un enfoque geométrico basado en celdas de Dirichlet y un enfoque probabilístico basado en una métrica de “bola vecina más próxima”. ${\displaystyle \mathbb {R} ^{k}(k>1)}$

Véase también

• Divergencia de Kullback-Leibler
• Máxima verosimilitud
• Distribución de probabilidad

Notas

1. Parece haber algunos errores tipográficos menores en el artículo. Por ejemplo, en la sección 4.2, ecuación (4.1), el reemplazo de redondeo para , no debería tener el término logarítmico. En la sección 1, la ecuación (1.2), se define como el espaciado en sí mismo, y es la suma negativa de los logaritmos de . Si se registra en este paso, el resultado siempre es ≤ 0, ya que la diferencia entre dos puntos adyacentes en una distribución acumulativa siempre es ≤ 1, y estrictamente < 1 a menos que solo haya dos puntos en los extremos. Además, en la sección 4.3, en la página 392, el cálculo muestra que es la varianza la que tiene una estimación de MPS de 6,87, no la desviación estándar . – Editor ${\displaystyle D_{j}}$ ${\displaystyle D_{j}}$ ${\displaystyle M(\theta )}$ ${\displaystyle D_{j}}$ ${\displaystyle D_{j}}$ ${\displaystyle \textstyle {\tilde {\sigma ^{2}}}}$ ${\displaystyle \textstyle {\tilde {\sigma }}}$
2. La literatura hace referencia a estadísticas relacionadas como estadísticas de Moran o Moran-Darling. Por ejemplo, Cheng y Stephens (1989) analizan la forma donde se define como se indica anteriormente. Wong y Li (2006) también utilizan la misma forma. Sin embargo, Beirlant y col. (2001) utilizan la forma , con el factor adicional de dentro de la suma logarítmica. Los factores adicionales marcarán una diferencia en términos de la media y la varianza esperadas de la estadística. Para mantener la coherencia, este artículo seguirá utilizando la forma Cheng y Amin/Wong y Li. -- Editor ${\displaystyle \scriptstyle M(\theta )=-\sum _{j=1}^{n+1}\log {D_{i}(\theta )}}$ ${\displaystyle \scriptstyle D_{i}(\theta )}$ ${\displaystyle \scriptstyle M_{n}=-\sum _{j=0}^{n}\ln {((n+1)(X_{n,i+1}-X_{n,i}))}}$ ${\displaystyle (n+1)}$
3. Wong y Li (2006) excluyen la constante de Euler-Mascheroni de su descripción. -- Editor

Referencias

Citas

1. Cheng y Amin (1983)
2. Ranneby (1984)
3. Hall y otros (2004)
4. Anatolyev y Kosenok (2004)
5. Piedra (2014)
6. Wong y Li (2006)
7. Pike (1965)
8. Cheng y Stephens (1989)

Obras citadas

• Anatolyev, Stanislav; Kosenok, Grigory (2005). "Una alternativa a la máxima verosimilitud basada en espaciamientos" (PDF) . Teoría econométrica . 21 (2): 472–476. CiteSeerX  10.1.1.494.7340 . doi :10.1017/S0266466605050255. S2CID  123004317. Archivado desde el original (PDF) el 2011-08-16 . Consultado el 2009-01-21 .
• Beirlant, J.; Dudewicz, EJ; Györfi, L.; van der Meulen, EC (1997). "Estimación de entropía no paramétrica: una visión general" (PDF) . Revista Internacional de Ciencias Matemáticas y Estadísticas . 6 (1): 17–40. ISSN  1055-7490. Archivado desde el original (PDF) el 5 de mayo de 2005 . Consultado el 31 de diciembre de 2008 . Nota: el artículo vinculado es una versión actualizada de 2001.
• Cheng, RCH; Amin, NAK (1983). "Estimación de parámetros en distribuciones univariadas continuas con un origen desplazado". Revista de la Royal Statistical Society, Serie B . 45 (3): 394–403. doi :10.1111/j.2517-6161.1983.tb01268.x. ISSN  0035-9246. JSTOR  2345411.
• Cheng, RCH; Stephens, MA (1989). "Una prueba de bondad de ajuste utilizando la estadística de Moran con parámetros estimados". Biometrika . 76 (2): 386–392. doi :10.1093/biomet/76.2.385.
• Ekström, Magnus (1997). "Generalized maximum spacing estimate". Universidad de Umeå, Departamento de Matemáticas . 6. ISSN  0345-3928. Archivado desde el original el 14 de febrero de 2007. Consultado el 30 de diciembre de 2008 .
• Hall, MJ; van den Boogaard, HFP; Fernando, RC; Mynett, AE (2004). "La construcción de intervalos de confianza para el análisis de frecuencias utilizando técnicas de remuestreo". Hidrología y Ciencias del Sistema Terrestre . 8 (2): 235–246. doi : 10.5194/hess-8-235-2004 . ISSN  1027-5606.
• Pieciak, Tomasz (2014). Estimación del ruido de espaciado máximo en datos de resonancia magnética de fondo de bobina única. IEEE International Conference on Image Processing. París. págs. 1743–1747. doi :10.1109/icip.2014.7025349.
• Pyke, Ronald (1965). "Espaciados". Revista de la Royal Statistical Society, Serie B . 27 (3): 395–449. doi :10.1111/j.2517-6161.1965.tb00602.x. ISSN  0035-9246. JSTOR  2345793.
• Ranneby, Bo (1984). "El método de espaciado máximo. Un método de estimación relacionado con el método de máxima verosimilitud". Scandinavian Journal of Statistics . 11 (2): 93–112. ISSN  0303-6898. JSTOR  4615946.
• Ranneby, Bo; Ekström, Magnus (1997). " Estimaciones de espaciado máximo basadas en diferentes métricas". Universidad de Umeå, Departamento de Matemáticas . 5. ISSN  0345-3928. Archivado desde el original el 14 de febrero de 2007. Consultado el 30 de diciembre de 2008 .
• Ranneby, Bo; Jammalamadakab, S. Rao; Teterukovskiy, Alex (2005). "La estimación del espaciado máximo para observaciones multivariadas" (PDF) . Journal of Statistical Planning and Inference . 129 (1–2): 427–446. doi :10.1016/j.jspi.2004.06.059 . Consultado el 31 de diciembre de 2008 .
• Wong, TST; Li, WK (2006). "Una nota sobre la estimación de distribuciones de valores extremos utilizando el producto máximo de espaciamientos". Series de tiempo y temas relacionados: en memoria de Ching-Zong Wei . Apuntes de clase del Instituto de Estadística Matemática – Serie de monografías. Beachwood, Ohio: Instituto de Estadística Matemática. págs. 272–283. arXiv : math/0702830v1 . doi :10.1214/074921706000001102. ISBN . 978-0-940600-68-3.S2CID88516426  .​