El análisis de balance de flujo ( FBA ) es un método matemático para simular el metabolismo de células u organismos unicelulares completos, como E. coli o levadura, utilizando reconstrucciones a escala del genoma de redes metabólicas . Las reconstrucciones a escala del genoma describen todas las reacciones bioquímicas en un organismo basándose en su genoma completo. Estas reconstrucciones modelan el metabolismo centrándose en las interacciones entre metabolitos, identificando qué metabolitos están involucrados en las diversas reacciones que tienen lugar en una célula u organismo y determinando los genes que codifican las enzimas que catalizan estas reacciones (si las hay). En comparación con los métodos tradicionales de modelado, FBA es menos intensivo en términos de los datos de entrada necesarios para construir el modelo. Las simulaciones realizadas con FBA son computacionalmente económicas y pueden calcular flujos metabólicos en estado estacionario para modelos grandes (más de 10,000 reacciones) en unos pocos segundos en computadoras personales modernas. El método relacionado de análisis de vías metabólicas busca encontrar y enumerar todas las vías posibles entre metabolitos.
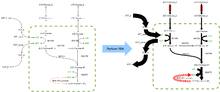
El FBA encuentra aplicaciones en la ingeniería de bioprocesos para identificar sistemáticamente modificaciones en las redes metabólicas de los microbios utilizados en los procesos de fermentación que mejoran los rendimientos de los productos químicos de importancia industrial como el etanol y el ácido succínico. [2] También se ha utilizado para la identificación de posibles dianas farmacológicas en el cáncer [3] y los patógenos, [4] el diseño racional de medios de cultivo [5] y las interacciones huésped-patógeno . [6] Los resultados del FBA se pueden visualizar para redes más pequeñas utilizando mapas de flujo similares a la imagen de la derecha, que ilustra los flujos de estado estacionario transportados por las reacciones en la glucólisis . El grosor de las flechas es proporcional al flujo a través de la reacción.
El método FBA formaliza el sistema de ecuaciones que describe los cambios de concentración en una red metabólica como el producto escalar de una matriz de coeficientes estequiométricos (la matriz estequiométrica S ) y el vector v de los flujos no resueltos. El lado derecho del producto escalar es un vector de ceros que representa el sistema en estado estacionario . En estado estacionario, las concentraciones de metabolitos permanecen constantes a medida que las tasas de producción y consumo están equilibradas, lo que da como resultado que no haya cambios netos a lo largo del tiempo. Dado que el sistema de ecuaciones suele estar subdeterminado, puede haber múltiples soluciones posibles. Para obtener una única solución, se selecciona el flujo que maximiza una reacción de interés, como la producción de biomasa o ATP. A continuación, se utiliza la programación lineal para calcular una de las posibles soluciones de los flujos correspondientes al estado estacionario.
Algunos de los primeros trabajos sobre el análisis de equilibrio de flujo se remontan a principios de los años 1980. Papoutsakis [7] demostró que era posible construir ecuaciones de equilibrio de flujo utilizando un mapa metabólico. Sin embargo, fue Watson [8] quien introdujo por primera vez la idea de utilizar la programación lineal y una función objetivo para calcular los flujos en una vía. El primer estudio significativo fue publicado posteriormente por Fell y Small [9] , quienes utilizaron el análisis de equilibrio de flujo junto con funciones objetivo más elaboradas para estudiar las limitaciones en la síntesis de grasas.






El análisis de biomasa no requiere un gran esfuerzo computacional, ya que se necesitan unos segundos para calcular los flujos óptimos para la producción de biomasa para una red típica (alrededor de 10 000 reacciones). Esto significa que el efecto de eliminar reacciones de la red o cambiar las restricciones de flujo se puede modelar de manera sensata en una sola computadora.
Una técnica que se utiliza con frecuencia para buscar en una red metabólica reacciones que son particularmente críticas para la producción de biomasa. Al eliminar cada reacción de una red y medir el flujo previsto a través de la función de biomasa o cualquier otro objetivo, como la producción de ATP, cada reacción se puede clasificar como esencial (si el flujo a través de la función de biomasa se reduce sustancialmente) o no esencial (si el flujo a través de la función de biomasa no cambia o solo se reduce ligeramente).
La eliminación de reacciones por pares de todos los pares posibles de reacciones es útil cuando se buscan dianas farmacológicas, ya que permite la simulación de tratamientos con múltiples dianas, ya sea con un solo fármaco con múltiples dianas o con combinaciones de fármacos. Los estudios de doble eliminación también pueden cuantificar las interacciones letales sintéticas entre diferentes vías, lo que proporciona una medida de la contribución de la vía a la solidez general de la red.
Los genes están conectados a reacciones catalizadas por enzimas mediante expresiones booleanas conocidas como expresiones de reacción gen-proteína (GPR). Normalmente, una GPR toma la forma (gen A y gen B) para indicar que los productos de los genes A y B son subunidades proteicas que se ensamblan para formar la proteína completa y, por lo tanto, la ausencia de cualquiera de ellos daría como resultado la eliminación de la reacción. Por otro lado, si la GPR es (gen A o gen B), implica que los productos de los genes A y B son isoenzimas , lo que significa que la expresión de cualquiera de ellos es suficiente para mantener una reacción activa. Una reacción también puede estar regulada por un solo gen o, en el caso de la difusión, puede no estar asociada con ningún gen en absoluto. Por lo tanto, es posible evaluar el efecto de la eliminación de un solo gen o de varios mediante la evaluación de la GPR como una expresión booleana. Si la GPR se evalúa como falso , la reacción se restringe a cero en el modelo antes de realizar la FBA. Por lo tanto, las eliminaciones de genes se pueden simular utilizando la FBA. Lógicamente no se pueden eliminar las reacciones que no están asociadas a ningún gen.
La utilidad de los análisis de inhibición de la reacción y de eliminación se hace más evidente si se ha ensamblado una matriz de reacción de gen-proteína para la red que se está estudiando con FBA. La matriz de reacción de gen-proteína es una matriz binaria que conecta los genes con las proteínas que se forman a partir de ellos. Utilizando esta matriz, la esencialidad de la reacción se puede convertir en esencialidad del gen indicando los defectos genéticos que pueden causar un cierto fenotipo de enfermedad o las proteínas/enzimas que son esenciales (y por lo tanto qué enzimas son los objetivos farmacológicos más prometedores en los patógenos). Sin embargo, la matriz de reacción de gen-proteína no especifica la relación booleana entre los genes con respecto a la enzima, sino que simplemente indica una asociación entre ellos. Por lo tanto, debe utilizarse solo si la expresión booleana de GPR no está disponible.
El efecto de inhibir una reacción, en lugar de eliminarla por completo, se puede simular en FBA restringiendo el flujo permitido a través de ella. El efecto de una inhibición se puede clasificar como letal o no letal aplicando los mismos criterios que en el caso de una deleción, donde se utiliza un umbral adecuado para distinguir entre “sustancialmente reducida” y “ligeramente reducida”. Generalmente, la elección del umbral es arbitraria, pero se puede obtener una estimación razonable a partir de experimentos de crecimiento donde se realizan las inhibiciones/deleciones simuladas y se mide la tasa de crecimiento.
Para diseñar medios de crecimiento óptimos con respecto a tasas de crecimiento mejoradas o secreción de subproductos útiles, es posible utilizar un método conocido como análisis del plano de fase fenotípico. PhPP implica aplicar FBA repetidamente en el modelo mientras se covarían las restricciones de absorción de nutrientes y se observa el valor de la función objetivo (o flujos de subproductos). PhPP hace posible encontrar la combinación óptima de nutrientes que favorecen un fenotipo particular o un modo de metabolismo que resulta en tasas de crecimiento más altas o secreción de subproductos industrialmente útiles. Se ha demostrado que las tasas de crecimiento previstas de bacterias en diferentes medios se correlacionan bien con los resultados experimentales, [10] así como para definir medios mínimos precisos para el cultivo de Salmonella typhimurium . [11]
Interacciones huésped-patógeno
La microbiota humana es un sistema complejo con hasta 400 billones de microbios y bacterias que interactúan entre sí y con el huésped. Para comprender los factores clave de este sistema, se propone un análisis de equilibrio de flujo dinámico y multiescala, ya que el análisis de equilibrio de flujo se clasifica como menos intensivo en términos computacionales. [12]
A diferencia del enfoque tradicionalmente seguido de modelado metabólico utilizando ecuaciones diferenciales ordinarias acopladas , el análisis de balance de flujo requiere muy poca información en términos de los parámetros cinéticos de las enzimas y la concentración de metabolitos en el sistema. Esto se logra haciendo dos suposiciones, estado estacionario y optimalidad. La primera suposición es que el sistema modelado ha entrado en un estado estacionario, donde las concentraciones de metabolitos ya no cambian, es decir, en cada nodo de metabolito los flujos de producción y consumo se cancelan entre sí. La segunda suposición es que el organismo ha sido optimizado a través de la evolución para algún objetivo biológico, como el crecimiento óptimo o la conservación de recursos. La suposición de estado estacionario reduce el sistema a un conjunto de ecuaciones lineales, que luego se resuelve para encontrar una distribución de flujo que satisface la condición de estado estacionario sujeta a las restricciones de estequiometría mientras maximiza el valor de una pseudorreacción (la función objetivo) que representa la conversión de precursores de biomasa en biomasa.
El supuesto de estado estable se remonta a las ideas de equilibrio de materiales desarrolladas para modelar el crecimiento de células microbianas en fermentadores en la ingeniería de bioprocesos. Durante el crecimiento microbiano, se consume un sustrato que consiste en una mezcla compleja de fuentes de carbono, hidrógeno, oxígeno y nitrógeno junto con oligoelementos para generar biomasa. El modelo de equilibrio de materiales para este proceso se convierte en:
Si consideramos que el sistema de células microbianas se encuentra en estado estacionario, podemos establecer el término de acumulación en cero y reducir las ecuaciones de balance de materiales a ecuaciones algebraicas simples. En un sistema de este tipo, el sustrato se convierte en la entrada del sistema, que se consume, y la biomasa se produce y se convierte en la salida del sistema. El balance de materiales puede representarse entonces como:
Matemáticamente, las ecuaciones algebraicas se pueden representar como un producto escalar de una matriz de coeficientes y un vector de incógnitas. Dado que el supuesto de estado estacionario pone el término de acumulación en cero, el sistema se puede escribir como:
Extendiendo esta idea a las redes metabólicas, es posible representar una red metabólica como un conjunto de ecuaciones balanceadas estequiométricamente. Pasando al formalismo matricial, podemos representar las ecuaciones como el producto escalar de una matriz de coeficientes estequiométricos (matriz estequiométrica ) y el vector de flujos como las incógnitas y establecer el lado derecho en 0, lo que implica el estado estacionario.
Las redes metabólicas suelen tener más reacciones que metabolitos y esto da como resultado un sistema indeterminado de ecuaciones lineales que contiene más variables que ecuaciones. El enfoque estándar para resolver estos sistemas indeterminados es aplicar la programación lineal .
Los programas lineales son problemas que pueden expresarse en forma canónica :
donde x representa el vector de variables (a determinar), c y b son vectores de coeficientes (conocidos), A es una matriz (conocida) de coeficientes y es la matriz transpuesta . La expresión a maximizar o minimizar se denomina función objetivo ( c T x en este caso). Las desigualdades A x ≤ b son las restricciones que especifican un politopo convexo sobre el que se optimizará la función objetivo.
La programación lineal requiere la definición de una función objetivo. La solución óptima para el problema de programación lineal se considera la solución que maximiza o minimiza el valor de la función objetivo según el caso en cuestión. En el caso del análisis de balance de flujo, la función objetivo Z para la programación lineal se define a menudo como la producción de biomasa. La producción de biomasa se simula mediante una ecuación que representa una reacción concentrada que convierte varios precursores de biomasa en una unidad de biomasa.
Por lo tanto, la forma canónica de un problema de análisis de balance de flujo sería:
donde representa el vector de flujos (a determinar), es una matriz (conocida) de coeficientes. La expresión a maximizar o minimizar se denomina función objetivo ( en este caso). Las desigualdades y definen, respectivamente, las tasas mínimas y máximas de flujo para cada reacción correspondiente a las columnas de la matriz. Estas tasas se pueden determinar experimentalmente para restringir y mejorar aún más la precisión predictiva del modelo o se pueden especificar a un valor arbitrariamente alto que indique que no hay restricción en el flujo a través de la reacción.
La principal ventaja del enfoque del balance de flujo es que no requiere ningún conocimiento de las concentraciones de metabolitos o, lo que es más importante, de la cinética enzimática del sistema; el supuesto de homeostasis excluye la necesidad de conocer las concentraciones de metabolitos en cualquier momento siempre que esa cantidad permanezca constante y, además, elimina la necesidad de leyes de velocidad específicas, ya que supone que en estado estacionario no hay cambios en el tamaño del conjunto de metabolitos en el sistema. Los coeficientes estequiométricos por sí solos son suficientes para la maximización matemática de una función objetivo específica .
La función objetivo es esencialmente una medida de cómo cada componente del sistema contribuye a la producción del producto deseado. El producto en sí depende del propósito del modelo, pero uno de los ejemplos más comunes es el estudio de la biomasa total. Un ejemplo notable del éxito de la FBA es la capacidad de predecir con precisión la tasa de crecimiento de la procariota E. coli cuando se cultiva en diferentes condiciones. [10] En este caso, el sistema metabólico se optimizó para maximizar la función objetivo de biomasa. Sin embargo, este modelo se puede utilizar para optimizar la producción de cualquier producto y, a menudo, se utiliza para determinar el nivel de salida de algún producto biotecnológicamente relevante. El modelo en sí se puede verificar experimentalmente cultivando organismos utilizando un quimiostato o herramientas similares para garantizar que las concentraciones de nutrientes se mantengan constantes. Las mediciones de la producción del objetivo deseado se pueden utilizar entonces para corregir el modelo.
Una buena descripción de los conceptos básicos de FBA se puede encontrar en el material complementario de libre acceso de Edwards et al. 2001 [10] que se puede encontrar en el sitio web de Nature. [13] Otras fuentes incluyen el libro "Systems Biology" de B. Palsson dedicado al tema [14] y un útil tutorial y artículo de J. Orth. [15] Existen muchas otras fuentes de información sobre la técnica en la literatura científica publicada, incluyendo Lee et al. 2006, [16] Feist et al. 2008, [17] y Lewis et al. 2012. [18]
Las partes clave de la preparación del modelo son: crear una red metabólica sin espacios, agregar restricciones al modelo y, finalmente, agregar una función objetivo (a menudo llamada función de biomasa), generalmente para simular el crecimiento del organismo que se está modelando.

Las redes metabólicas pueden variar en alcance desde aquellas que describen una sola vía , hasta la célula , el tejido o el organismo . El requisito principal de una red metabólica que forma la base de una red preparada para FBA es que no contenga lagunas. Esto normalmente significa que se requiere una extensa curación manual, lo que hace que la preparación de una red metabólica para el análisis de balance de flujo sea un proceso que puede llevar meses o años. Sin embargo, los avances recientes, como los denominados métodos de relleno de lagunas, pueden reducir el tiempo necesario a semanas o meses.
Los paquetes de software para la creación de modelos FBA incluyen: Pathway Tools/MetaFlux, [19] [20] Simpheny, [21] [22] MetNetMaker, [23] COBRApy, [24] CarveMe, [25] MIOM, [26] o COBREXA.jl. [27]
Generalmente, los modelos se crean en formato BioPAX o SBML para que se puedan realizar análisis o visualizaciones posteriores en otro software, aunque esto no es un requisito.
Una parte clave del análisis de la red metabólica es la capacidad de agregar restricciones a las tasas de flujo de las reacciones dentro de las redes, obligándolas a permanecer dentro de un rango de valores seleccionados. Esto permite que el modelo simule con mayor precisión el metabolismo real. Las restricciones pertenecen a dos subconjuntos desde una perspectiva biológica: restricciones de límite que limitan la absorción/excreción de nutrientes y restricciones internas que limitan el flujo a través de las reacciones dentro del organismo. En términos matemáticos, se puede considerar la aplicación de restricciones para reducir el espacio de soluciones del modelo de análisis de la red metabólica. Además de las restricciones aplicadas en los bordes de una red metabólica, se pueden aplicar restricciones a las reacciones en las profundidades de la red. Estas restricciones suelen ser simples; pueden restringir la dirección de una reacción debido a consideraciones energéticas o restringir la velocidad máxima de una reacción debido a la velocidad finita de todas las reacciones en la naturaleza.
Los organismos, y todos los demás sistemas metabólicos, requieren de algún aporte de nutrientes. Normalmente, la velocidad de absorción de nutrientes está determinada por su disponibilidad (un nutriente que no está presente no puede ser absorbido), su concentración y sus constantes de difusión (las concentraciones más altas de metabolitos que se difunden rápidamente se absorben más rápidamente) y el método de absorción (como el transporte activo o la difusión facilitada frente a la difusión simple).
Si la tasa de absorción (y/o excreción) de ciertos nutrientes se puede medir experimentalmente, entonces esta información se puede agregar como una restricción a la tasa de flujo en los bordes de un modelo metabólico. Esto garantiza que los nutrientes que no están presentes o que no son absorbidos por el organismo no ingresen a su metabolismo (la tasa de flujo se limita a cero) y también significa que la simulación respeta las tasas de absorción de nutrientes conocidas. Esto proporciona un método secundario para asegurarse de que el metabolismo simulado tenga propiedades verificadas experimentalmente en lugar de solo aceptables matemáticamente.
En principio, todas las reacciones son reversibles, pero en la práctica, las reacciones suelen producirse en una sola dirección. Esto puede deberse a una concentración de reactivos significativamente mayor en comparación con la concentración de productos de la reacción. Pero, con mayor frecuencia, esto sucede porque los productos de una reacción tienen una energía libre mucho menor que los reactivos y, por lo tanto, se favorece más la dirección de la reacción hacia adelante.
Para reacciones ideales,
Para ciertas reacciones se puede aplicar una restricción termodinámica que implica dirección (en este caso hacia adelante)
De manera realista, el flujo a través de una reacción no puede ser infinito (dado que las enzimas en el sistema real son finitas), lo que implica que,
Ciertas tasas de flujo se pueden medir experimentalmente ( ) y los flujos dentro de un modelo metabólico se pueden restringir, dentro de cierto error ( ), para garantizar que estas tasas de flujo conocidas se reproduzcan con precisión en la simulación.
La forma más sencilla de medir las tasas de flujo de absorción de nutrientes es en el borde de la red. Es posible medir los flujos internos utilizando metabolitos marcados radiactivamente o visibles por RMN.
Los modelos metabólicos preparados para FBA restringidos se pueden analizar utilizando software como la caja de herramientas COBRA [28] (implementaciones disponibles en MATLAB y Python ), SurreyFBA [29] o FAME basado en la web. [30] Se han enumerado paquetes de software adicionales en otros lugares. [31] Recientemente se ha revisado exhaustivamente todo este software y sus funcionalidades. [32]
Una alternativa de código abierto está disponible en R (lenguaje de programación) como los paquetes abcdeFBA o sybil [33] para realizar FBA y otras técnicas de modelado basadas en restricciones. [34]
El análisis de la biomasa puede proporcionar un gran número de soluciones matemáticamente aceptables para el problema del estado estacionario . Sin embargo, las soluciones de interés biológico son las que producen los metabolitos deseados en la proporción correcta. La función objetivo define la proporción de estos metabolitos. Por ejemplo, cuando se modela el crecimiento de un organismo, la función objetivo se define generalmente como biomasa. Matemáticamente, es una columna en la matriz estequiométrica cuyas entradas colocan una "demanda" o actúan como un "sumidero" para los precursores biosintéticos como los ácidos grasos, los aminoácidos y los componentes de la pared celular que están presentes en las filas correspondientes de la matriz S. Estas entradas representan proporciones de peso seco de componentes celulares medidas experimentalmente. Por lo tanto, esta columna se convierte en una reacción concentrada que simula el crecimiento y la reproducción. Por lo tanto, la precisión de las mediciones experimentales juega un papel esencial en la definición correcta de la función de biomasa y hace que los resultados del análisis de la biomasa sean biológicamente aplicables al garantizar que el metabolismo produzca la proporción correcta de metabolitos.
Al modelar redes más pequeñas, la función objetivo se puede modificar en consecuencia. Un ejemplo de esto sería el estudio de las vías metabólicas de los carbohidratos , donde la función objetivo probablemente se definiría como una determinada proporción de ATP y NADH y, por lo tanto, simularía la producción de metabolitos de alta energía por esta vía.
La programación lineal se puede utilizar para encontrar una única solución óptima. El objetivo de optimización biológica más común para una red metabólica de todo el organismo sería elegir el vector de flujo que maximice el flujo a través de una función de biomasa compuesta por los metabolitos constituyentes del organismo colocados en la matriz estequiométrica y denotados o simplemente
En el caso más general, se puede definir cualquier reacción y añadirla a la función de biomasa con la condición de que se maximice o minimice si se desea una única solución “óptima”. Alternativamente, y en el caso más general, se puede introducir un vector que defina el conjunto ponderado de reacciones que el modelo de programación lineal debe intentar maximizar o minimizar.
En el caso de que exista una única función/reacción de biomasa independiente dentro de la matriz estequiométrica, se simplificaría a todos ceros con un valor de 1 (o cualquier valor distinto de cero) en la posición correspondiente a esa función de biomasa. Cuando existieran múltiples funciones objetivo independientes, se simplificaría a todos ceros con valores ponderados en las posiciones correspondientes a todas las funciones objetivo.
El análisis del espacio nulo de matrices se implementa en paquetes de software especializados para operaciones matriciales como Matlab y Octave. La determinación del espacio nulo de nos dice todas las posibles colecciones de vectores de flujo (o combinaciones lineales de los mismos) que equilibran los flujos dentro de la red biológica. La ventaja de este enfoque se hace evidente en los sistemas biológicos que se describen mediante sistemas de ecuaciones diferenciales con muchas incógnitas. Las velocidades en las ecuaciones diferenciales anteriores - y - dependen de las velocidades de reacción de las ecuaciones subyacentes. Las velocidades se toman generalmente de la teoría cinética de Michaelis-Menten , que involucra los parámetros cinéticos de las enzimas que catalizan las reacciones y la concentración de los propios metabolitos. Aislar enzimas de organismos vivos y medir sus parámetros cinéticos es una tarea difícil, como lo es medir las concentraciones internas y las constantes de difusión de los metabolitos dentro de un organismo. Por lo tanto, el enfoque de ecuaciones diferenciales para el modelado metabólico está más allá del alcance actual de la ciencia para todos, excepto los organismos más estudiados. [35] La FBA evita este impedimento aplicando el supuesto homeostático, que es una descripción razonablemente aproximada de los sistemas biológicos.
Aunque el análisis de flujo funcional evita ese obstáculo biológico, sigue existiendo el problema matemático de un gran espacio de soluciones. El análisis de flujo funcional tiene un doble propósito: representar con precisión los límites biológicos del sistema y devolver la distribución de flujo más cercana a los flujos naturales dentro del sistema/organismo objetivo. Ciertos principios biológicos pueden ayudar a superar las dificultades matemáticas. Si bien la matriz estequiométrica casi siempre está subdeterminada inicialmente (lo que significa que el espacio de soluciones es muy grande), el tamaño del espacio de soluciones se puede reducir y hacer que refleje mejor la biología del problema mediante la aplicación de ciertas restricciones a las soluciones.
El éxito de FBA y la comprensión de sus limitaciones han llevado a extensiones que intentan mediar las limitaciones de la técnica.

La solución óptima para el problema del equilibrio de flujo rara vez es única, ya que existen muchas soluciones posibles e igualmente óptimas. El análisis de variabilidad de flujo (FVA), integrado en algunos programas de análisis, devuelve los límites de los flujos a través de cada reacción que, junto con la combinación correcta de otros flujos, pueden estimar la solución óptima.

Las reacciones que pueden soportar una baja variabilidad de flujos a través de ellas probablemente sean de mayor importancia para un organismo y FVA es una técnica prometedora para la identificación de reacciones que son importantes.
Al simular knockouts o crecimiento en medios, el análisis de bioquímica funcional (FBA) proporciona la distribución de flujo en estado estacionario final. Este estado estacionario final se alcanza en escalas de tiempo variables. Por ejemplo, la tasa de crecimiento prevista de E. coli en glicerol como fuente primaria de carbono no coincidió con las predicciones del análisis de bioquímica funcional; sin embargo, al realizar un subcultivo durante 40 días o 700 generaciones, la tasa de crecimiento evolucionó de manera adaptativa para coincidir con la predicción del análisis de bioquímica funcional. [36]
A veces resulta interesante averiguar cuál es el efecto inmediato de una perturbación o eliminación, ya que lleva tiempo que se produzcan cambios regulatorios y que el organismo reorganice los flujos para utilizar de manera óptima una fuente de carbono diferente o evitar el efecto de la eliminación. MOMA predice la distribución de flujo subóptima inmediata después de la perturbación al minimizar la distancia (euclidiana) entre la distribución de flujo de FBA de tipo salvaje y la distribución de flujo de mutante mediante programación cuadrática. Esto produce un problema de optimización de la forma.
donde representa la distribución de flujo de tipo salvaje (o estado no perturbado) y representa la distribución de flujo en la eliminación de genes que se debe resolver. Esto se simplifica a:
Esta es la solución MOMA que representa la distribución del flujo inmediatamente después de la perturbación. [37]
ROOM intenta mejorar la predicción del estado metabólico de un organismo después de una eliminación de un gen. Sigue la misma premisa que MOMA de que un organismo intentaría restaurar una distribución de flujo lo más cercana posible al tipo salvaje después de una eliminación. Sin embargo, plantea además la hipótesis de que este estado estable se alcanzaría a través de una serie de cambios metabólicos transitorios por parte de la red reguladora y que el organismo intentaría minimizar la cantidad de cambios regulatorios necesarios para alcanzar el estado de tipo salvaje. Sin embargo, en lugar de utilizar una minimización de métricas de distancia, utiliza un método de programación lineal entera mixta. [38]
El análisis de factibilidad dinámico intenta agregar la capacidad de que los modelos cambien con el tiempo, evitando así, de alguna manera, la estricta condición de estado estable del análisis de factibilidad puro. Por lo general, la técnica implica ejecutar una simulación de factibilidad, cambiar el modelo en función de los resultados de esa simulación y volver a ejecutar la simulación. Al repetir este proceso, se logra un elemento de retroalimentación con el tiempo.
El análisis de FBA proporciona un análisis menos simplista que el análisis de puntos de estrangulamiento, pero requiere mucha menos información sobre las tasas de reacción y una reconstrucción de red mucho menos completa que la que requeriría una simulación dinámica completa. Para cubrir esta necesidad, se ha demostrado que el análisis de FBA es una técnica muy útil para el análisis de las capacidades metabólicas de los sistemas celulares.
A diferencia del análisis de puntos de estrangulamiento, que solo considera los puntos de la red donde se producen metabolitos pero no se consumen o viceversa, el análisis de puntos de estrangulamiento es una verdadera forma de modelado de redes metabólicas porque considera la red metabólica como una entidad única y completa ( la matriz estequiométrica ) en todas las etapas del análisis. Esto significa que los efectos de red, como las reacciones químicas en vías distantes que se afectan entre sí, se pueden reproducir en el modelo. La ventaja de la incapacidad del análisis de puntos de estrangulamiento para simular los efectos de red es que considera cada reacción dentro de una red de forma aislada y, por lo tanto, puede sugerir reacciones importantes en una red incluso si una red está muy fragmentada y contiene muchos huecos.
A diferencia de la simulación metabólica dinámica, la FBA supone que la concentración interna de metabolitos dentro de un sistema se mantiene constante a lo largo del tiempo y, por lo tanto, no puede proporcionar nada más que soluciones de estado estable. Es poco probable que la FBA pueda, por ejemplo, simular el funcionamiento de una célula nerviosa. Dado que la concentración interna de metabolitos no se considera dentro de un modelo, es posible que una solución FBA pueda contener metabolitos en una concentración demasiado alta para ser biológicamente aceptable. Este es un problema que las simulaciones metabólicas dinámicas probablemente evitarían. Una ventaja de la simplicidad de la FBA sobre las simulaciones dinámicas es que son mucho menos costosas computacionalmente, lo que permite la simulación de un gran número de perturbaciones en la red. Una segunda ventaja es que el modelo reconstruido puede ser sustancialmente más simple al evitar la necesidad de considerar las tasas de enzimas y el efecto de interacciones complejas en la cinética enzimática.
{{cite web}}: CS1 maint: archived copy as title (link)