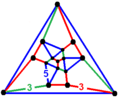
En geometría , un dodecaedro tetraédricamente disminuido (también icosaedro tetraédricamente estrellado o tetraedro propelente [1] ) es un poliedro topológicamente autodual formado por 16 vértices, 30 aristas y 16 caras (4 triángulos equiláteros y 12 cuadriláteros idénticos ). [2]
Existe una forma canónica con dos longitudes de arista en 0,849 : 1,057, asumiendo que el radio de la esfera media es 1. Las cometas siguen siendo isósceles.
Tiene simetría tetraédrica quiral , por lo que su geometría puede construirse a partir de la simetría piritoédrica del pseudoicosaedro de 4 caras estrelladas , o bien a partir del piritoedro , de 4 vértices disminuidos . Dentro de su simetría tetraédrica , tiene proporciones geométricas variadas. Por la construcción dual de Dorman Luke , se puede definir una proporción geométrica única. Las caras de la cometa tienen aristas con una relación de longitud de ~1:0,633.
Topológicamente, los triángulos son siempre equiláteros, mientras que los cuadriláteros son irregulares, aunque las dos aristas adyacentes que se encuentran en los vértices de un tetraedro sean iguales.
Como hexadecaedro autodual , es una de las 302404 formas, 1476 con simetría al menos de orden 2 y la única con simetría tetraédrica. [3]
Como dodecaedro regular disminuido , con 4 vértices eliminados, las caras del cuadrilátero son trapecios .
Como estelación del icosaedro regular, es una de las 32 estelaciones definidas con simetría tetraédrica. Tiene caras de cometa. [4]
En la notación de poliedro de Conway , se puede representar como pT , aplicando el operador de hélice de George W. Hart a un tetraedro regular . [5]
Este poliedro representa la figura de vértice de un panal uniforme hiperbólico , el panal icosaédrico parcialmente disminuido , pd{3,5,3}, con 12 antiprismas pentagonales y 4 celdas dodecaédricas que se encuentran en cada vértice.