Regla de Littlewood-Richardson

En matemáticas , la regla de Littlewood-Richardson es una descripción combinatoria de los coeficientes que surgen al descomponer un producto de dos funciones de Schur como una combinación lineal de otras funciones de Schur. Estos coeficientes son números naturales, que la regla de Littlewood-Richardson describe como contar ciertos cuadros sesgados . Ocurren en muchos otros contextos matemáticos, por ejemplo como multiplicidad en la descomposición de productos tensoriales de representaciones de dimensión finita de grupos lineales generales , o en la descomposición de ciertas representaciones inducidas en la teoría de la representación del grupo simétrico , o en el área de Combinatoria algebraica que trata con cuadros de Young y polinomios simétricos .

Los coeficientes de Littlewood-Richardson dependen de tres particiones , digamos , de las cuales y describen las funciones de Schur que se multiplican, y dan la función de Schur de la cual este es el coeficiente en la combinación lineal; en otras palabras son los coeficientes tales que ${\displaystyle \lambda ,\mu ,\nu }$ ${\displaystyle \lambda }$ ${\displaystyle \mu }$ ${\displaystyle \nu }$ ${\displaystyle c_{\lambda ,\mu }^{\nu }}$

${\displaystyle s_{\lambda }s_{\mu }=\sum _{\nu }c_{\lambda ,\mu }^{\nu }s_{\nu }.}$

La regla de Littlewood-Richardson establece que es igual al número de cuadros de Littlewood-Richardson de forma sesgada y de peso . ${\displaystyle c_{\lambda ,\mu }^{\nu }}$ ${\displaystyle \nu /\lambda }$ ${\displaystyle \mu }$

Historia

Desgraciadamente, la regla de Littlewood-Richardson es mucho más difícil de demostrar de lo que se sospechaba en un principio. Una vez le dijeron al autor que la regla de Littlewood-Richardson ayudó a que los hombres llegaran a la luna, pero no se demostró hasta que llegaron allí.

Gordon James (1987)

La regla de Littlewood-Richardson fue establecida por primera vez por DE Littlewood y AR Richardson  (1934, teorema III p. 119), pero aunque la afirmaron como un teorema, sólo la demostraron en algunos casos especiales bastante simples. Robinson  (1938) afirmó haber completado su prueba, pero su argumento tenía lagunas, aunque estaba escrito de manera tan oscura que dichas lagunas no se notaron durante algún tiempo, y su argumento se reproduce en el libro (Littlewood 1950). Algunas de las lagunas fueron posteriormente colmadas por Macdonald (1995). Las primeras pruebas rigurosas de la regla fueron dadas cuatro décadas después de su hallazgo, por Schützenberger (1977) y Thomas (1974), después de que C. Schensted  (1961), Schützenberger (1963) y Knuth  ( 1963 ) desarrollaran la necesaria teoría combinatoria ( 1970) en su trabajo sobre la correspondencia Robinson-Schensted . En la actualidad existen varias pruebas breves de la regla, como (Gasharov 1998) y (Stembridge 2002) que utilizan involuciones de Bender-Knuth . Littelmann (1994) utilizó el modelo de ruta de Littelmann para generalizar la regla de Littlewood-Richardson a otros grupos de Lie semisimples.

La regla de Littlewood-Richardson es conocida por la cantidad de errores que aparecieron antes de su prueba completa y publicada. Varios intentos publicados para demostrarlo son incompletos, y es particularmente difícil evitar errores al hacer cálculos manuales con él: incluso el ejemplo original de DE Littlewood y AR Richardson (1934) contiene un error.

Cuadros de Littlewood-Richardson

Un cuadro de Littlewood-Richardson

Un cuadro de Littlewood-Richardson es un cuadro semiestándar sesgado con la propiedad adicional de que la secuencia obtenida al concatenar sus filas invertidas es una palabra reticular (o permutación reticular), lo que significa que en cada parte inicial de la secuencia cualquier número ocurre al menos con la misma frecuencia. como el número . Otra caracterización equivalente (aunque no del todo obvia) es que el cuadro en sí, y cualquier cuadro obtenido a partir de él eliminando algunas de sus columnas situadas más a la izquierda, tiene un peso ligeramente decreciente. Se han encontrado muchas otras nociones combinatorias que resultan estar en biyección con los cuadros de Littlewood-Richardson y, por lo tanto, también pueden usarse para definir los coeficientes de Littlewood-Richardson. ${\displaystyle i}$ ${\displaystyle i+1}$

Otro cuadro de Littlewood-Richardson

Ejemplo

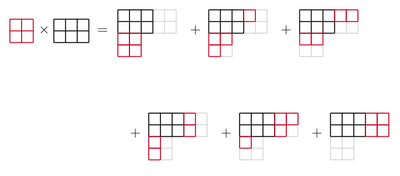
Considere el caso de que , y . Entonces, el hecho de que esto se pueda deducir del hecho de que los dos cuadros que se muestran a la derecha son los únicos dos cuadros de Littlewood-Richardson en cuanto a forma y peso . De hecho, dado que el último cuadro de la primera línea no vacía del diagrama de asimetría sólo puede contener una entrada 1, toda la primera línea debe llenarse con las entradas 1 (esto es cierto para cualquier cuadro de Littlewood-Richardson); en el último cuadro de la segunda fila solo podemos colocar un 2 por el rigor de la columna y el hecho de que nuestra palabra de celosía no puede contener ninguna entrada más grande antes de que contenga un 2. Para el primer cuadro de la segunda fila ahora podemos usar un 1 o un 2. Una vez elegida esa entrada, la tercera fila debe contener las entradas restantes para hacer el peso (3,2,1), en un orden débilmente creciente, por lo que ya no nos queda otra opción; en ambos casos resulta que encontramos un cuadro de Littlewood-Richardson. ${\displaystyle \lambda =(2,1)}$ ${\displaystyle \mu =(3,2,1)}$ ${\displaystyle \nu =(4,3,2)}$ ${\displaystyle c_{\lambda ,\mu }^{\nu }=2}$ ${\displaystyle \nu /\lambda }$ ${\displaystyle \mu }$

Una descripción más geométrica

La condición de que la secuencia de entradas leídas del cuadro en un orden algo peculiar forme una palabra reticular puede ser reemplazada por una condición más local y geométrica. Dado que en un cuadro semiestándar nunca aparecen entradas iguales en la misma columna, se pueden numerar las copias de cualquier valor de derecha a izquierda, que es su orden de aparición en la secuencia que debería ser una palabra reticular. Llame al número así asociado a cada entrada su índice y escriba una entrada i con índice j como i [ j ]. Ahora bien, si algún cuadro de Littlewood-Richardson contiene una entrada con índice j , entonces esa entrada i [ j ] debería aparecer en una fila estrictamente debajo de la de (lo que ciertamente también ocurre, ya que la entrada i  − 1 ocurre al menos con tanta frecuencia como la entrada Yo lo hago). De hecho, la entrada i [ j ] también debería aparecer en una columna no más a la derecha de esa misma entrada (lo que a primera vista parece ser una condición más estricta). Si el peso del cuadro de Littlewood-Richardson se fija de antemano, entonces se puede formar una colección fija de entradas indexadas, y si éstas se colocan de manera que respeten esas restricciones geométricas, además de las de los cuadros semiestándar y la condición de que las copias indexadas de las mismas entradas deben respetar el orden de los índices de derecha a izquierda, entonces se garantiza que los cuadros resultantes serán cuadros de Littlewood-Richardson. ${\displaystyle i>1}$ ${\displaystyle (i-1)[j]}$ ${\displaystyle (i-1)[j]}$

Una forma algorítmica de la regla.

El Littlewood-Richardson, como se indicó anteriormente, proporciona una expresión combinatoria para los coeficientes individuales de Littlewood-Richardson, pero no da ninguna indicación de un método práctico para enumerar los cuadros de Littlewood-Richardson con el fin de encontrar los valores de estos coeficientes. De hecho, por supuesto, no existe un criterio simple para determinar si existen cuadros de forma y peso de Littlewood-Richardson (aunque hay una serie de condiciones necesarias, la más simple de las cuales es ); por lo tanto, parece inevitable que en algunos casos uno tenga que realizar una búsqueda elaborada, sólo para descubrir que no existen soluciones. ${\displaystyle \lambda ,\mu ,\nu }$ ${\displaystyle \nu /\lambda }$ ${\displaystyle \mu }$ ${\displaystyle |\lambda |+|\mu |=|\nu |}$

Sin embargo, la regla conduce a un procedimiento bastante eficiente para determinar la descomposición completa de un producto de funciones de Schur, en otras palabras, para determinar todos los coeficientes para λ y μ fijos, pero ν variables. Esto fija el peso de los cuadros de Littlewood-Richardson que se van a construir y la "parte interior" λ de su forma, pero deja la "parte exterior" ν libre. Como se conoce el peso, el conjunto de entradas indexadas en la descripción geométrica es fijo. Ahora, para entradas indexadas sucesivas, se pueden probar todas las posiciones posibles permitidas por las restricciones geométricas en una búsqueda de retroceso . Las entradas se pueden probar en orden creciente, mientras que entre entradas iguales se pueden probar mediante índice decreciente . Este último punto es la clave para la eficiencia del procedimiento de búsqueda: la entrada i [ j ] se restringe a estar en una columna a la derecha de , pero no más a la derecha que (si dichas entradas están presentes). Esto restringe fuertemente el conjunto de posiciones posibles, pero siempre deja al menos una posición válida para ; por lo tanto, cada ubicación de una entrada dará lugar al menos a un cuadro completo de Littlewood-Richardson, y el árbol de búsqueda no contiene callejones sin salida. ${\displaystyle c_{\lambda ,\mu }^{\nu }}$ ${\displaystyle i[j+1]}$ ${\displaystyle i-1[j]}$ ${\displaystyle i[j]}$

Se puede utilizar un método similar para encontrar todos los coeficientes para λ y ν fijos, pero variables en μ. ${\displaystyle c_{\lambda ,\mu }^{\nu }}$

Coeficientes de Littlewood-Richardson

Los coeficientes de Littlewood-Richardson c^νλμ
_​   aparecen de las siguientes maneras interrelacionadas:

• Son las constantes de estructura del producto en el anillo de funciones simétricas con respecto a la base de las funciones de Schur.

${\displaystyle s_{\lambda }s_{\mu }=\sum c_{\lambda \mu }^{\nu }s_{\nu }}$

o equivalente c^νλμ
_​   es el producto interno de s _ν y s _λ s _μ .

• Expresan funciones de Schur sesgadas en términos de funciones de Schur

${\displaystyle s_{\nu /\lambda }=\sum _{\mu }c_{\lambda \mu }^{\nu }s_{\mu }.}$

• La C^νλμ
  _​   aparecen como números de intersección en un Grassmanniano :

${\displaystyle \sigma _{\lambda }\sigma _{\mu }=\sum c_{\lambda \mu }^{\nu }\sigma _{\nu }}$

donde σ _μ es la clase de la variedad Schubert de un Grassmanniano correspondiente a  μ .

• C^νλμ
  _​   es el número de veces la representación irreducible V _λ ⊗ V _μ del producto de grupos simétricos S _{| λ |} × S _{| µ |} aparece en la restricción de la representación V _ν de S _{| y |} a S _{| λ |} × S _{| µ |} . Según la reciprocidad de Frobenius, este es también el número de veces que V _ν ocurre en la representación de S _{| y |} inducido desde V _λ  ⊗  V _μ .
• La C^νλμ
  _​   aparecen en la descomposición del producto tensorial (Fulton 1997) de dos módulos de Schur (representaciones irreducibles de grupos lineales especiales)

${\displaystyle E^{\lambda }\otimes E^{\mu }=\bigoplus _{\nu }(E^{\nu })^{\oplus c_{\lambda \mu }^{\nu }}.}$

• C^νλμ
  _​   es el número de cuadros estándar de Young de forma ν / μ que son jeu de taquin equivalentes a algún cuadro estándar fijo de Young de forma  λ .
• C^νλμ
  _​   es el número de cuadros de Littlewood-Richardson de forma ν / λ y de peso  μ .
• C^νλμ
  _​   es el número de imágenes entre μ y ν/λ.

Casos especiales

La fórmula de Pieri.

La fórmula de Pieri , que es el caso especial de la regla de Littlewood-Richardson en el caso en que una de las particiones tiene solo una parte , establece que

${\displaystyle S_{\mu }S_{n}=\sum _{\lambda }S_{\lambda }}$

donde S _n es la función de Schur de una partición con una fila y la suma es sobre todas las particiones λ obtenidas de μ agregando n elementos a su diagrama de Ferrers , no hay dos en la misma columna.

Particiones rectangulares

Si ambas particiones son de forma rectangular , la suma también está libre de multiplicidad (Okada 1998). Fije a , b , p y q enteros positivos con p q . Denota por la partición con p partes de longitud a . Las particiones que indexan componentes no triviales son aquellas particiones con una longitud tal que ${\displaystyle \geq }$ ${\displaystyle (a^{p})}$ ${\displaystyle s_{(a^{p})}s_{(b^{q})}}$ ${\displaystyle \lambda }$ ${\displaystyle \leq p+q}$

• ${\displaystyle \lambda _{q+1}=\lambda _{q+2}=\cdots =\lambda _{p}=a,}$
• ${\displaystyle \lambda _{q}\geq \mathrm {max} (a,b)}$
• ${\displaystyle \lambda _{i}+\lambda _{p+q-i+1}=a+b,\quad {i=1,\dots ,q}.}$

Por ejemplo,

.

Generalizaciones

Coeficientes de Kronecker reducidos del grupo simétrico.

El coeficiente de Kronecker reducido del grupo simétrico es una generalización de tres diagramas de Young arbitrarios , que es simétrico bajo permutaciones de los tres diagramas. ${\displaystyle {\bar {C}}_{\lambda ,\mu ,\nu }}$ ${\displaystyle c_{\lambda ,\mu }^{\nu }}$ ${\displaystyle \lambda ,\mu ,\nu }$

Funciones sesgadas de Schur

Zelevinsky (1981) amplió la regla de Littlewood-Richardson para sesgar las funciones de Schur de la siguiente manera:

${\displaystyle s_{\lambda }s_{\mu /\nu }=\sum _{\lambda +\omega (T_{\geq j})\in P}s_{\lambda +\omega (T)}}$

donde la suma es sobre todos los cuadros T en μ/ν de modo que para todos j , la secuencia de números enteros λ+ω( T _{≥ j} ) no es creciente y ω es el peso.

Números de Newell-Littlewood

Los números de Newell-Littlewood se definen a partir de los coeficientes de Littlewood-Richardson mediante la expresión cúbica ^[1]

${\displaystyle N_{\mu ,\nu ,\lambda }=\sum _{\alpha ,\beta ,\gamma }c_{\alpha ,\beta }^{\mu }c_{\alpha ,\gamma }^{\nu }c_{\beta ,\gamma }^{\lambda }}$

Los números de Newell-Littlewood dan algunas de las multiplicidades de productos tensoriales de representaciones de dimensión finita de grupos de Lie clásicos de los tipos . ${\displaystyle B,C,D}$

La condición de no desaparición en los tamaños de los diagramas de Young conduce a ${\displaystyle c_{\lambda ,\mu }^{\nu }\neq 0\implies |\lambda |+|\mu |=|\nu |}$

${\displaystyle N_{\mu ,\nu ,\lambda }\neq 0\implies \left\{{\begin{array}{l}||\lambda |-|\mu ||\leq |\nu |\leq |\lambda |+|\mu |\\|\lambda |+|\mu |+|\nu |\in 2\mathbb {Z} \end{array}}\right.}$

Los números de Newell-Littlewood son generalizaciones de los coeficientes de Littlewood-Richardson en el sentido de que

${\displaystyle |\mu |+|\nu |=|\lambda |\implies N_{\mu ,\nu ,\lambda }=c_{\mu ,\nu }^{\lambda }}$

Los números de Newell-Littlewood que involucran un diagrama de Young con una sola fila obedecen una regla de tipo Pieri: es el número de formas de eliminar cuadros de (de diferentes columnas) y luego agregar cuadros (a diferentes columnas) para hacer . ^[1] ${\displaystyle N_{(k),\mu ,\nu }}$ ${\displaystyle {\frac {k+|\mu |-|\nu |}{2}}}$ ${\displaystyle \mu }$ ${\displaystyle {\frac {k-|\mu |+|\nu |}{2}}}$ ${\displaystyle \nu }$

Los números de Newell-Littlewood son las constantes de estructura de un álgebra asociativa y conmutativa cuyos elementos base son particiones, con el producto . Por ejemplo, ${\displaystyle \mu \times \nu =\sum _{\lambda }N_{\mu ,\nu ,\lambda }\lambda }$

${\displaystyle (1)\times (k)=(k-1)+(k+1)+(k,1)\quad {\text{(Newell–Littlewood)}}}$

${\displaystyle (1)\times (k)=(k+1)+(k,1)\quad {\text{(Littlewood–Richardson)}}}$

Ejemplos

Los ejemplos de coeficientes de Littlewood-Richardson a continuación se dan en términos de productos de polinomios de Schur S _π , indexados por particiones π, usando la fórmula

${\displaystyle S_{\lambda }S_{\mu }=\sum c_{\lambda \mu }^{\nu }S_{\nu }.}$

Todos los coeficientes con como máximo 4 vienen dados por: ${\displaystyle |\nu |}$

• S ₀ S _π = S _π para cualquier π. donde S ₀ =1 es el polinomio de Schur de la partición vacía
• S ₁ S ₁ = S ₂ + S ₁₁
• S ₂ S ₁ = S ₃ + S ₂₁
• S ₁₁ S ₁ = S ₁₁₁ + S ₂₁
• S ₃ S ₁ = S ₄ + S ₃₁
• S ₂₁ S ₁ = S ₃₁ + S ₂₂ + S ₂₁₁
• S ₂ S ₂ = S ₄ + S ₃₁ + S ₂₂
• S ₂ S ₁₁ = S ₃₁ + S ₂₁₁
• S ₁₁₁ S ₁ = S ₁₁₁₁ + S ₂₁₁
• S ₁₁ S ₁₁ = S ₁₁₁₁ + S ₂₁₁ + S ₂₂

La mayoría de los coeficientes para particiones pequeñas son 0 o 1, lo que ocurre en particular cuando uno de los factores es de la forma S _n o S _11...1 , debido a la fórmula de Pieri y su contraparte transpuesta. El ejemplo más simple con un coeficiente mayor que 1 ocurre cuando ninguno de los factores tiene esta forma:

• S ₂₁ S ₂₁ = S ₄₂ + S ₄₁₁ + S ₃₃ + 2 S ₃₂₁ + S ₃₁₁₁ + S ₂₂₂ + S ₂₂₁₁ .

Para particiones más grandes, los coeficientes se vuelven más complicados. Por ejemplo,

• S ₃₂₁ S ₃₂₁ = S ₆₄₂ + S ₆₄₁₁ + S ₆₃₃ +2 S ₆₃₂₁ + S ₆₃₁₁₁ + S ₆₂₂₂ + S ₆₂₂₁₁ + S ₅₅₂ + S ₅₅₁₁ +2 S ₅₄₃ +4 S ₅₄₂₁ +2 S ₅₄₁₁₁ +3 S ₅₃₃₁ +3 S ₅₃₂₂ +4 S ₅₃₂₁₁ + S ₅₃₁₁₁₁ +2 S ₅₂₂₂₁ + S ₅₂₂₁₁₁ + S ₄₄₄ +3 S ₄₄₃₁ +2 S ₄₄₂₂ +3 S ₄₄₂₁₁ + S ₄₄₁₁₁₁ +3 S ₄₃₃₂ +3 S ₄₃₃₁₁ +4 S ₄₃₂₂₁ +2 S ₄₃₂₁₁₁ + S ₄₂₂₂₂ + S ₄₂₂₂₁₁ + S ₃₃₃₃ +2 S ₃₃₃₂₁ + S ₃₃₃₁₁₁ + S ₃₃₂₂₂ + S ₃₃₂₂₁₁ con 34 términos y multiplicidad total 62, y el coeficiente más grande es 4
• S ₄₃₂₁ S ₄₃₂₁ es una suma de 206 términos con una multiplicidad total de 930 y el coeficiente más grande es 18.
• S ₅₄₃₂₁ S ₅₄₃₂₁ es una suma de 1433 términos con multiplicidad total 26704, y el coeficiente más grande (el de S _86543211 ) es 176.
• S ₆₅₄₃₂₁ S ₆₅₄₃₂₁ es una suma de 10873 términos con una multiplicidad total de 1458444 (por lo que el valor promedio de los coeficientes es superior a 100 y pueden ser tan grandes como 2064).

El ejemplo original dado por Littlewood y Richardson (1934, p. 122-124) fue (después de corregir 3 cuadros que encontraron pero olvidaron incluir en la suma final)

• S ₄₃₁ S ₂₂₁ = S ₆₅₂ + S ₆₅₁₁ + S ₆₄₃ + 2 S ₆₄₂₁ + S ₆₄₁₁₁ + S ₆₃₃₁ + S 6322 + S ₆₃₂₁₁ + S ₅₅₃ + 2 _S 5521 + _S 55111 + ₂ S 5431 ₊ 2 S ₅₄₂₂ + 3 S ₅₄₂₁₁ + S ₅₄₁₁₁₁ + S ₅₃₃₂ + S ₅₃₃₁₁ + 2 S ₅₃₂₂₁ + S ₅₃₂₁₁₁ + S ₄₄₃₂ + S ₄₄₃₁₁ + 2 S ₄₄₂₂₁ + S ₄₄₂₁₁₁ + S ₄₃₃₂₁ + S ₄₃₂₂₂ + S ₄₃₂₂₁₁

con 26 términos provenientes de los siguientes 34 cuadros:

....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11 ...22 ...22 ...2 ...2 ...2 ...2 ... ... ....3 . .23 .2 .3 . .22 .2 .2  3 3 2 2 3 23 2  3 3....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ...12 ...12 ...12 ...12 ...2 ...1 ...1 ...2 ...1.23 .2 .3 . .13 .22 .2 .1 .2  3 2 2 2 3 23 23 2 3 3....1 ....1 ....1 ....1 ....1 ....1 ....1 ....1 ...2 ...2 ...2 ... ... ... ... ... .1 .3 . .12 .12 .1 .2 .2 2 1 1 23 2 22 13 13 2 2 3 3 2 2 3 3.... .... .... .... .... .... .... .... ...1 ...1 ...1 ...1 ...1 ... ... ... .12 .12 .1 .2 .2 .11 .1 .1 23 2 22 13 1 22 12 12 3 3 2 2 3 23 2 3 3

El cálculo de funciones de Schur sesgadas es similar. Por ejemplo, los 15 cuadros de Littlewood-Richardson para ν=5432 y λ=331 son

...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 .. .11 ...11 ...11...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 ...2 .. .2 ...2 ...2.11 .11 .11 .12 .11 .12 .13 .13 .23 .13 .13 .12 .12 .23 .2312 13 22 12 23 13 12 24 14 14 22 23 33 13 34

entonces S _5432/331 = Σ c^νλμ
_​  S _μ = S ₅₂ + S ₅₁₁ + S ₄₁₁₁ + S ₂₂₂₁ + 2 S ₄₃ + 2 S ₃₂₁₁ + 2 S ₃₂₂ + 2 S ₃₃₁ + 3 S ₄₂₁ (Fulton 1997, p. 64).

Notas

1. Gao, Shiliang; Orelowitz, Gidon; Yong, Alejandro (2021). "Números de Newell-Littlewood". Trans. América. Matemáticas. Soc . 374 (9): 6331–6366. arXiv : 2005.09012v1 . doi : 10.1090/tran/8375. S2CID  218684561.

Referencias

• Fulton, William (1997), Cuadros jóvenes , Textos estudiantiles de la London Mathematical Society, vol. 35, Cambridge University Press , pág. 121, ISBN 978-0-521-56144-0, señor  1464693
• Gasharov, Vesselin (1998), "Una breve prueba de la regla de Littlewood-Richardson", European Journal of Combinatorics , 19 (4): 451–453, doi : 10.1006/eujc.1998.0212 , ISSN  0195-6698, MR  1630540
• James, Gordon (1987), "La teoría de la representación de los grupos simétricos", The Arcata Conference on Representations of Finite Groups (Arcata, California, 1986) , Proc. Simposios. Matemáticas puras, vol. 47, Providence, RI: Sociedad Matemática Estadounidense , págs. 111–126, SEÑOR  0933355
• Knuth, Donald E. (1970), "Permutaciones, matrices y cuadros de Young generalizados", Pacific Journal of Mathematics , 34 (3): 709–727, doi : 10.2140/pjm.1970.34.709 , ISSN  0030-8730, SEÑOR  0272654
• Littelmann, Peter (1994), "Una regla de Littlewood-Richardson para álgebras de Kac-Moody simetrizables" (PDF) , Invent. Matemáticas. , 116 : 329–346, Bibcode : 1994InMat.116..329L, doi : 10.1007/BF01231564, S2CID  85546837
• Littlewood, Dudley E. (1950), La teoría de los caracteres grupales y las representaciones matriciales de grupos, AMS Chelsea Publishing, Providence, RI, ISBN 978-0-8218-4067-2, SEÑOR  0002127
• Littlewood, DE; Richardson, AR (1934), "Group Characters and Algebra", Transacciones filosóficas de la Royal Society de Londres. Serie A, que contiene artículos de carácter matemático o físico , 233 (721–730), The Royal Society: 99–141, Bibcode :1934RSPTA.233...99L, doi : 10.1098/rsta.1934.0015 , ISSN  0264-3952, JSTOR  91293
• Macdonald, IG (1995), Funciones simétricas y polinomios de Hall, Oxford Mathematical Monographs (2ª ed.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853489-1, MR  1354144, archivado desde el original el 11 de diciembre de 2012
• Okada, Soichi (1998), "Aplicaciones de fórmulas de suma menor a representaciones de grupos clásicos de forma rectangular", Journal of Algebra , 205 (2): 337–367, doi : 10.1006/jabr.1997.7408 , ISSN  0021-8693, SEÑOR  1632816
• Robinson, G. de B. (1938), "Sobre las representaciones del grupo simétrico", American Journal of Mathematics , 60 (3), The Johns Hopkins University Press: 745–760, doi :10.2307/2371609, ISSN  0002- 9327, JSTOR  2371609 Zbl 0019.25102
• Schensted, C. (1961), "Subsecuencias crecientes y decrecientes más largas", Canadian Journal of Mathematics , 13 : 179–191, doi : 10.4153/CJM-1961-015-3 , ISSN  0008-414X, MR  0121305
• Schützenberger, MP (1963), "Quelques remarques sur une Construction de Schensted", Mathematica Scandinavica , 12 : 117–128, doi : 10.7146/math.scand.a-10676 , ISSN  0025-5521, MR  0190017
• Schützenberger, Marcel-Paul (1977), "La correspondencia de Robinson", Combinatoire et représentation du groupe symétrique (Actes Table Ronde CNRS, Univ. Louis-Pasteur Estrasburgo, Estrasburgo, 1976) , Lecture Notes in Mathematics, vol. 579, Berlín, Nueva York: Springer-Verlag , págs. 59-113, doi :10.1007/BFb0090012, ISBN 978-3-540-08143-2, señor  0498826
• Stembridge, John R. (2002), "Una prueba concisa de la regla de Littlewood-Richardson" (PDF) , Electronic Journal of Combinatorics , 9 (1): Nota 5, 4 págs. (electrónica), doi : 10.37236/1666 , ISSN  1077-8926, SEÑOR  1912814
• Thomas, Glânffrwd P. (1974), Álgebras de Baxter y funciones de Schur , Ph.D. Tesis, Swansea: University College of Swansea
• van Leeuwen, Marc AA (2001), "La regla de Littlewood-Richardson y la combinatoria relacionada" (PDF) , Interacción de la combinatoria y la teoría de la representación , MSJ Mem., vol. 11, Tokio: Matemáticas. Soc. Japón, págs. 95 a 145, MR  1862150
• Zelevinsky, AV (1981), "Una generalización de la regla de Littlewood-Richardson y la correspondencia Robinson-Schensted-Knuth", Journal of Algebra , 69 (1): 82–94, doi : 10.1016/0021-8693(81)90128 -9 , ISSN  0021-8693, SEÑOR  0613858

enlaces externos

• Un programa en línea que descompone productos de funciones de Schur utilizando la regla de Littlewood-Richardson