
La cobertura biológica ocurre cuando los organismos sufren una disminución de su aptitud en sus condiciones típicas a cambio de una mayor aptitud en condiciones estresantes. La cobertura biológica se propuso originalmente para explicar la observación de un banco de semillas , o un reservorio de semillas no germinadas en el suelo. [1] Por ejemplo, la aptitud de una planta anual se maximiza para ese año si todas sus semillas germinan. Sin embargo, si ocurre una sequía que mata las plantas germinadas, pero no las semillas no germinadas, las plantas con semillas que permanecen en el banco de semillas tendrán una ventaja de aptitud. Por lo tanto, puede ser ventajoso para las plantas "cubrir sus apuestas" en caso de una sequía produciendo algunas semillas que germinen inmediatamente y otras semillas que permanezcan inactivas. Otros ejemplos de cobertura biológica incluyen el apareamiento múltiple femenino , [2] el comportamiento de búsqueda de alimento en abejorros , [3] el almacenamiento de nutrientes en rizobios , [4] y la persistencia bacteriana en presencia de antibióticos. [5]

Hay tres categorías (estrategias) de cobertura de apuestas: cobertura de apuestas "conservadora", cobertura de apuestas "diversificada" y "lanzamiento de moneda adaptativo".
En la estrategia de cobertura de apuestas conservadora, los individuos reducen su aptitud física esperada a cambio de una menor varianza en la aptitud física. La idea de esta estrategia es que un organismo “siempre juegue a lo seguro” utilizando la misma estrategia exitosa de bajo riesgo independientemente de las condiciones ambientales. [6] Un ejemplo de esto sería un organismo que produce puestas con un tamaño de huevo constante que puede no ser óptimo para cualquier condición ambiental, pero que da como resultado la varianza general más baja. [6]
A diferencia de la estrategia de cobertura de apuestas conservadora, la estrategia de cobertura de apuestas diversificada se produce cuando los individuos reducen su aptitud física esperada en un año determinado y al mismo tiempo aumentan la varianza de supervivencia entre las crías. Esta estrategia utiliza la idea de no "poner todos los huevos en una canasta". [6] Los individuos que implementan esta estrategia en realidad invierten en varias estrategias diferentes a la vez, lo que da como resultado una baja variación en el éxito a largo plazo. Esto podría demostrarse mediante una nidada de huevos de diferentes tamaños, cada uno óptimo para un entorno potencial de la descendencia. Si bien esto significa que la descendencia especializada para otro entorno tiene menos probabilidades de sobrevivir hasta la edad adulta, también protege contra la posibilidad de que ninguna descendencia sobreviva hasta el año siguiente. [6]
Un individuo que utiliza este tipo de cobertura de apuestas elige qué estrategia utilizar en función de una predicción de cómo será el entorno. Los organismos que utilizan esta forma de cobertura de apuestas hacen estas predicciones y seleccionan estrategias anualmente. Por ejemplo, un organismo puede producir puestas de huevos de diferentes tamaños de un año a otro, lo que aumenta la variación en el éxito de la descendencia entre puestas. [6] A diferencia de las estrategias de cobertura de apuestas conservadoras y diversificadas, la estrategia de lanzamiento de moneda adaptativa no se preocupa por minimizar la variación en la aptitud entre años.
Para determinar si un alelo de cobertura de apuestas es el favorito, se debe comparar la aptitud a largo plazo de cada alelo. Particularmente en entornos altamente variables donde es probable que evolucione la cobertura de apuestas, la aptitud a largo plazo se mide mejor utilizando la media geométrica [7] , que es multiplicativa en lugar de aditiva como la media aritmética . La media geométrica es muy sensible a valores pequeños. Incluso las raras ocurrencias de aptitud cero para un genotipo dan como resultado que tenga una media geométrica esperada de cero. Esto lo hace apropiado para circunstancias en las que un solo genotipo puede tener una aptitud variable dependiendo de las circunstancias ambientales.
Se entiende que la cobertura de apuestas es un modo de respuesta al cambio ambiental. [8] Las adaptaciones que permiten a los organismos sobrevivir en condiciones ambientales fluctuantes proporcionan una ventaja evolutiva. Si bien un rasgo de cobertura de apuestas puede no ser óptimo para un entorno en particular, esto se ve compensado por los beneficios de una mayor aptitud en una variedad de entornos. Por lo tanto, los alelos de cobertura de apuestas tienden a ser favorecidos en entornos más variables. Para que un alelo de cobertura de apuestas se propague, debe persistir en el entorno típico a través de la deriva genética el tiempo suficiente para que se produzcan entornos alternativos, en los que el alelo que realiza la cobertura de apuestas tenga una ventaja sobre los genotipos adaptados al entorno anterior. A lo largo de muchas alteraciones ambientales posteriores, la selección puede arrastrar al alelo a la fijación. [9]
Un ejemplo común utilizado al describir la cobertura de apuestas es comparar la aptitud aritmética y geométrica entre genotipos especialistas y de cobertura de apuestas. [10] [11] La siguiente tabla muestra la aptitud relativa de cuatro fenotipos en años "buenos" y "malos" y sus respectivas medias si los años "buenos" ocurren el 75% del tiempo y los años "malos" el 25% del tiempo.
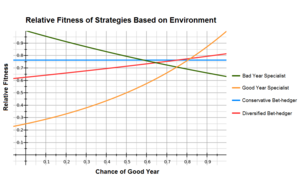
El especialista en buenos años tiene la mejor aptitud durante un buen año, pero le va muy mal durante un mal año, mientras que lo contrario es cierto para un especialista en malos años. El especialista en cobertura de apuestas conservadoras tiene el mismo rendimiento en todos los años y el especialista en cobertura de apuestas diversificadas en este ejemplo utiliza las dos estrategias de especialista el 50% del tiempo cada una; tienen un mejor rendimiento que el especialista en cobertura de apuestas conservadoras en los buenos años, pero peor durante un mal año.
En este ejemplo, la aptitud es aproximadamente igual en las estrategias de especialista y de cobertura de apuestas, y las de cobertura de apuestas tienen una aptitud significativamente mayor que la de los especialistas. Si bien el especialista de buen año tiene la media aritmética más alta, las estrategias de cobertura de apuestas siguen siendo las preferidas debido a su media geométrica más alta.
También es importante darse cuenta de que la idoneidad de cualquier estrategia depende de un gran número de factores, como la proporción de años buenos y malos y su idoneidad relativa entre años buenos y malos. Pequeños cambios en las estrategias o en el entorno tienen un gran impacto en cuál es la óptima. En el ejemplo anterior, el hedger de apuestas diversificadas supera al hedger de apuestas conservadoras si utiliza la estrategia del especialista en años buenos con más frecuencia. Por el contrario, si la idoneidad relativa del especialista en años buenos fue de 0,35 en un año malo, se convierte en la estrategia óptima.
Los experimentos de cobertura de apuestas con organismos modelo procariotas proporcionan algunas de las visiones más simplificadas de la evolución de la cobertura de apuestas. Como la cobertura de apuestas implica un cambio estocástico entre fenotipos a lo largo de generaciones, [12] los procariotas pueden mostrar este fenómeno bastante bien debido a su capacidad de reproducirse lo suficientemente rápido como para seguir la evolución en una sola población durante un corto período de tiempo. Esta rápida tasa de reproducción ha permitido el estudio de la cobertura de apuestas en laboratorios a través de modelos de evolución experimentales. Estos modelos se han utilizado para deducir los orígenes evolutivos de la cobertura de apuestas.
En el caso de los procariotas, existen numerosos ejemplos de cobertura de riesgo. En un ejemplo, la bacteria Sinorhizobium meliloti almacena carbono y energía en un compuesto conocido como poli-3-hidroxibutirato (PHB) para resistir entornos deficientes en carbono. Cuando se ven privadas de alimento, las poblaciones de S. meliloti comienzan a mostrar cobertura de riesgo al formar dos células hijas no idénticas durante la fisión binaria . Las células hijas muestran niveles bajos o altos de PHB, que son más adecuados para la inanición a corto y largo plazo, respectivamente. Se ha informado de que las células con niveles bajos de PHB deben competir eficazmente por los recursos para sobrevivir, mientras que las células con niveles altos de PHB pueden sobrevivir durante más de un año sin alimento. En este ejemplo, el fenotipo PHB está siendo "protegido", ya que la capacidad de supervivencia de la descendencia depende en gran medida de su entorno, donde solo es probable que sobreviva un fenotipo en condiciones específicas. [13]
Otro ejemplo de cobertura de apuestas surge en Mycobacterium tuberculosis . En una población dada de esta bacteria, existen células persistentes con la capacidad de detener su crecimiento, lo que las deja inafectadas por cambios dramáticos en el medio ambiente. Una vez que las células persistentes crecen para formar otra población de su especie, que puede o no ser resistente a los antibióticos , producirán células con crecimiento celular normal y otra población de persistentes para continuar este ciclo, según sea el caso. La capacidad de cambiar entre el fenotipo persistente y normal es una forma de cobertura de apuestas. [14]
Por lo tanto, la persistencia procariota como método de cobertura de riesgos es importante para el campo de la medicina debido a la persistencia bacteriana. Debido a que la cobertura de riesgos produce crías fenotípicamente diversas de manera aleatoria para sobrevivir en condiciones catastróficas, es difícil desarrollar tratamientos para las infecciones bacterianas, ya que la cobertura de riesgos puede garantizar la supervivencia de su especie dentro de su huésped, independientemente del antibiótico utilizado.
Los modelos eucariotas de cobertura de apuestas, a diferencia de los modelos procariotas, tienden a usarse para estudiar procesos evolutivos más complejos. En el contexto de los eucariotas, la cobertura de apuestas se utiliza mejor como una forma de analizar influencias ambientales complejas que afectan las presiones selectivas que subyacen al principio de cobertura de apuestas. Sin embargo, debido a que Eukarya es una categoría amplia, esta sección se ha subdividido en los reinos Animalia , Plantae y Fungi .
Por ejemplo, se ha planteado la hipótesis de que el salmón del Atlántico occidental ( Salmo salar ) tiene sistemas de apareamiento dependientes del complejo mayor de histocompatibilidad (CMH), que se ha demostrado que en otras especies es importante para determinar la resistencia a las enfermedades entre las crías. Es decir, hay evidencia de que la selección para una mayor diversidad del CMH es una fuerte influencia en la elección de pareja , donde se piensa que los individuos tienen más probabilidades de aparearse con individuos cuyo CMH es menos similar al suyo para producir una descendencia variable. De acuerdo con el modelo de cobertura de apuestas, se ha descubierto que el éxito reproductivo de las parejas de apareamiento del salmón del Atlántico depende del medio ambiente, donde ciertas construcciones del CMH solo son ventajosas en circunstancias ambientales específicas. Por lo tanto, esto apoya la evidencia de que la diversidad del CMH es crucial para el éxito reproductivo a largo plazo de los padres, ya que la compensación por una disminución inicial en la aptitud reproductiva a corto plazo está mediada por la supervivencia de algunas de sus crías en un entorno variable. [15]
Un segundo ejemplo entre los vertebrados es la especie marsupial Sminthopsis macrour , que utiliza una estrategia de letargo para reducir su tasa metabólica y sobrevivir a los cambios ambientales. Se ha demostrado que los ciclos de hormonas reproductivas median el momento del letargo y la reproducción, y en ratones se ha demostrado que median este proceso por completo, sin tener en cuenta el medio ambiente. En las especies marsupiales, sin embargo, se emplea un mecanismo adaptativo de lanzamiento de moneda en el que ni el letargo ni la reproducción se ven afectados por la manipulación de las hormonas, lo que sugiere que esta especie marsupial toma una decisión más activa sobre cuándo utilizar el letargo que se adapta mejor al entorno incierto en el que vive. [16]
Se sabe que muchas especies de invertebrados exhiben varias formas de cobertura de apuestas. Diaptomus sanguineus , una especie de crustáceo acuático que se encuentra en muchos estanques del noreste de los Estados Unidos, es uno de los ejemplos mejor estudiados de cobertura de apuestas. Esta especie utiliza una forma de cobertura de apuestas diversificada llamada banco de gérmenes, en el que el momento de emergencia entre las crías de una sola nidada es muy variable. Esto reduce los costos potenciales de un evento catastrófico durante un momento particularmente vulnerable en el desarrollo de la descendencia. En Diaptomus sanguineus , el banco de gérmenes ocurre cuando los padres producen huevos latentes antes de los cambios ambientales anuales que producen un mayor riesgo para el desarrollo de la descendencia. Por ejemplo, en estanques temporales, la producción de huevos latentes de Diaptomus sanguineus alcanza su punto máximo justo antes de la estación seca anual en junio, cuando los niveles de los estanques disminuyen. En estanques permanentes, la producción de huevos latentes aumenta en marzo, justo antes de un aumento anual en la actividad de alimentación de los peces luna. [17] Este ejemplo demuestra que el banco de gérmenes puede tomar diferentes formas dentro de una especie dependiendo del riesgo ambiental presentado. La cobertura de apuestas a través de patrones variables de eclosión de huevos también se observa en otros crustáceos. [18] [19]
También se ha observado la práctica de la cobertura de apuestas en los sistemas de apareamiento de algunas especies de arañas en invertebrados. Las hembras de la araña sierra domo ( Linyphia litigiosa ) son poliándricas y se aparean con machos secundarios para compensar la incertidumbre sobre la calidad de la pareja primaria. Se considera que las parejas primarias masculinas tienen una mayor aptitud que las masculinas secundarias, ya que las parejas primarias deben superar las luchas intrasexuales antes de aparearse con una hembra, mientras que las parejas masculinas secundarias se eligen mediante la elección de la hembra. Los científicos creen que la paternidad múltiple ha evolucionado en respuesta a la inseminación virgen por parte de parejas masculinas secundarias de baja calidad que no han sufrido una selección mediante luchas intrasexuales. Las hembras han desarrollado un mecanismo de precedencia de los espermatozoides para mantener el control sobre la paternidad de la descendencia y aumentar la aptitud de la descendencia. Un examen más detallado de los genitales femeninos ha apoyado esta hipótesis. La araña sierra domo exhibe este comportamiento como una forma de cobertura de apuestas genéticas, reduciendo el riesgo de producir descendencia de baja calidad y contraer enfermedades venéreas. [20] Esta forma de cobertura de apuestas es notablemente diferente de la mayoría de las otras formas de cobertura de apuestas, ya que no ha surgido en respuesta a las condiciones ambientales, sino que ha surgido como resultado del sistema de apareamiento de las especies.
La cobertura de bet se emplea en hongos de forma similar a las bacterias, pero en estos últimos es más compleja. Este fenómeno es beneficioso para los hongos, pero en algunos casos tiene efectos nocivos para los seres humanos, lo que demuestra que la cobertura de bet tiene importancia clínica. Un estudio sugiere que la cobertura de bet puede incluso contribuir al fracaso de la quimioterapia en el cáncer debido a mecanismos similares a los de la cobertura de bet utilizada en hongos. [21]
Una forma en que los hongos utilizan la estrategia de cobertura es mostrando diferentes morfologías de colonias cuando se cultivan en placas de agar. [22] Esta variación permite que las colonias tengan diferentes morfologías, incluidas las resistencias que les permiten sobrevivir, prosperar y reproducirse en diferentes condiciones o entornos. Como resultado, las infecciones por hongos pueden ser más difíciles de tratar si se utiliza la estrategia de cobertura. Por ejemplo, las cepas patógenas de levadura como Candida albicans o Candida glabrata que utilizan esta estrategia resistirán los tratamientos. Se sabe que estos hongos causan una infección conocida como candidiasis .
Si bien la cobertura de bet en hongos es importante, no se sabe mucho sobre los mecanismos de las diferentes estrategias empleadas por diferentes especies. Los investigadores han estudiado S. cerevisiae para determinar el mecanismo de cobertura de bet en esta especie. [22] Se determinó que en S. cerevisiae , existe variación en la distribución de las tasas de crecimiento entre las microcolonias de levadura y que el crecimiento lento es un predictor de la resistencia al calor. Tsl1 es un gen que se determinó como un factor en esta resistencia. Se demostró que la abundancia de este gen se correlaciona con la resistencia al calor y al estrés, y por lo tanto la supervivencia de las microcolonias de levadura en condiciones duras mediante el uso de cobertura de bet. Esto ilustra que al usar la cobertura de bet, las cepas patógenas de esta levadura que son dañinas para los humanos son más difíciles de tratar.
Un grupo de investigadores estudió otra forma de utilizar la cobertura de apuestas observando el hongo ascomiceto Neurospora crassa . [23] Se observó que esta especie produce ascosporas con variación en su latencia porque las ascosporas no latentes pueden morir por calor, pero las ascosporas latentes sobrevivirán. La única desventaja es que las ascosporas latentes tardarán más en germinar.
Las plantas proporcionan ejemplos sencillos para estudiar la estrategia de cobertura de apuestas en la vida silvestre, lo que permite realizar estudios de campo pero sin tantos factores de confusión como en el caso de los animales. El estudio de especies de plantas estrechamente relacionadas puede ayudarnos a comprender mejor las circunstancias en las que se desarrolla la estrategia de cobertura de apuestas.
El ejemplo clásico de cobertura de apuestas, la germinación tardía de las semillas, [1] ha sido ampliamente estudiado en plantas anuales del desierto. [24] [25] [26] Un estudio de campo de cuatro años [24] encontró que las poblaciones en entornos históricamente peores (más secos) tenían tasas de germinación más bajas. También encontraron una gran variedad de fechas de germinación y flexibilidad en la germinación para poblaciones más secas cuando se exponen a la lluvia, un fenómeno conocido como plasticidad fenotípica . Otros estudios de plantas anuales del desierto [25] [26] también han encontrado una relación entre la variación temporal y tasas de germinación más bajas. Uno de estos estudios [26] también encontró que la densidad de semillas en el banco de semillas afecta las tasas de germinación.
La cobertura de riesgos a través de un banco de semillas también se ha relacionado con la persistencia de las malezas. Un estudio [27] de veinte especies de malezas mostró que el porcentaje de semillas viables después de 5 años aumentó con la profundidad del suelo, y las tasas de germinación disminuyeron con la profundidad del suelo (aunque los números específicos variaron entre especies). Esto indica que las malezas participarán en la cobertura de riesgos a tasas más altas en circunstancias en las que los costos de la cobertura de riesgos son menores.
En las especies que se alimentan de semillas, la latencia de las semillas parece estar correlacionada "con un mayor contenido de polifenoles (flavonoides) en las cubiertas de las semillas, lo que da como resultado formas más oscuras (Gianella et al., 2021)". [ 28] En la Medicago truncatula , cuatro genes que controlan los flavonoides, además de las peroxidasas y las tio/peroxirredoxinas, "se han asociado con una latencia diferencial a lo largo de un gradiente de aridez (Renzi et al., 2020)". [28]
En conjunto, estos hallazgos proporcionan evidencia de la cobertura de apuestas en las plantas, pero también muestran la importancia de la competencia y la plasticidad fenotípica que los modelos simples de cobertura de apuestas a menudo ignoran.
Hasta el momento, la investigación sobre cobertura de apuestas que involucra a especies del dominio Archaea no ha sido fácilmente accesible.
La latencia de los virus del herpes se ha explicado mediante apuestas de cobertura . El virus de la varicela-zóster , por ejemplo, causa varicela en la primera infección y puede causar herpes zóster muchos años después de la infección original. El retraso con el que aparece el herpes zóster se ha explicado como una forma de apuestas de cobertura. [29]