El triángulo de Penrose , también conocido como tribar de Penrose , tribar imposible , [1] o triángulo imposible , [2] es un objeto imposible triangular , una ilusión óptica que consiste en un objeto que puede representarse en un dibujo en perspectiva. No puede existir como un objeto sólido en el espacio euclidiano tridimensional ordinario, aunque su superficie puede incrustarse isométricamente (doblarse pero no estirarse) en el espacio euclidiano de cinco dimensiones. [3] Fue creado por primera vez por el artista sueco Oscar Reutersvärd en 1934. [4] Independientemente de Reutersvärd, el triángulo fue ideado y popularizado en la década de 1950 por el psiquiatra Lionel Penrose y su hijo, el matemático y premio Nobel Roger Penrose , quien lo describió como "imposibilidad en su forma más pura". [5] Aparece de forma destacada en las obras del artista MC Escher , cuyas representaciones anteriores de objetos imposibles lo inspiraron en parte.
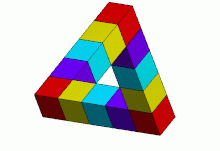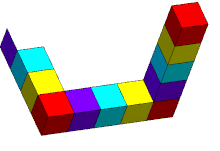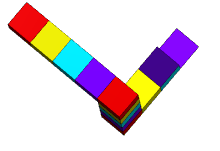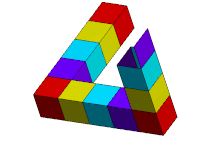
El triángulo parece ser un objeto sólido , formado por tres vigas rectas de sección transversal cuadrada que se unen en ángulo recto en los vértices del triángulo que forman. Las vigas pueden estar rotas, formando cubos o cuboides.
Esta combinación de propiedades no puede ser realizada por ningún objeto tridimensional en el espacio euclidiano ordinario . Un objeto así puede existir en ciertas variedades euclidianas tridimensionales . [6] Una superficie con las mismas distancias geodésicas que la superficie representada del tribar, pero sin que se conserven su forma plana y sus ángulos rectos, también puede existir en el espacio euclidiano de cinco dimensiones, que es el espacio euclidiano de menor dimensión dentro del cual esta superficie puede ser incrustada isométricamente. [3] También existen formas sólidas tridimensionales, cada una de las cuales, cuando se observa desde un cierto ángulo, parece igual a la representación bidimensional del triángulo de Penrose en esta página (como, por ejemplo, la imagen adyacente que representa una escultura en Perth , Australia ). El término "Triángulo de Penrose" puede referirse a la representación bidimensional o al objeto imposible en sí.
Si se traza una línea alrededor del triángulo de Penrose, se forma una banda de Möbius de cuatro bucles. [7]
La litografía Cascada (1961) de MC Escher representa un curso de agua que fluye en zigzag a lo largo de los lados largos de dos triángulos de Penrose alargados, de modo que termina dos pisos más alto que el punto de partida. La cascada resultante, que forma los lados cortos de ambos triángulos, impulsa una rueda hidráulica . Escher señala que para mantener la rueda en movimiento, ocasionalmente se debe agregar algo de agua para compensar la evaporación . Un tercer triángulo de Penrose se encuentra entre los otros dos, formado por dos segmentos de vía fluvial y una torre de soporte. [8]
![Triángulo de Penrose auténtico, de acero inoxidable, de WAStanggaßinger, Wasserburg am Inn, Alemania. Este tipo de triángulo imposible fue creado por primera vez en 1969 por el artista cinético soviético Vyacheslav Koleichuk.[9]](http://upload.wikimedia.org/wikipedia/commons/thumb/b/bf/Penrose_Triangle_auf_Ecke_stehend.jpg/1280px-Penrose_Triangle_auf_Ecke_stehend.jpg)