Analizador de energía electrónica hemisférico

Analizador de energía electrónica hemisférico.

Un analizador de energía electrónica hemisférico o analizador de deflexión hemisférica es un tipo de espectrómetro de energía electrónica que se utiliza generalmente para aplicaciones en las que se necesita una alta resolución energética: diferentes variedades de espectroscopia electrónica , como la espectroscopia de fotoemisión con resolución angular (ARPES), la espectroscopia fotoelectrónica de rayos X (XPS) y la espectroscopia electrónica Auger (AES) ^[1] o en aplicaciones de imágenes como la microscopía electrónica de fotoemisión (PEEM) y la microscopía electrónica de baja energía (LEEM). ^[2]

Consiste en dos hemisferios conductores concéntricos que sirven como electrodos que curvan las trayectorias de los electrones que entran en una ranura estrecha por un extremo, de modo que sus radios finales dependen de su energía cinética. El analizador, por lo tanto, proporciona una correlación de las energías cinéticas con las posiciones en un detector.

Función

Partes principales de un analizador de energía electrónica hemisférico.

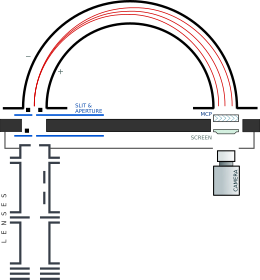
Un analizador hemisférico ideal consta de dos electrodos hemisféricos concéntricos (hemisferios interno y externo) de radios y mantenidos a voltajes adecuados. En un sistema de este tipo, los electrones se dispersan linealmente, dependiendo de su energía cinética, a lo largo de la dirección que conecta la rendija de entrada y la de salida, mientras que los electrones con la misma energía se concentran en primer orden. ^[3] ${\displaystyle R_{1}}$ ${\displaystyle R_{2}}$

Trayectorias calculadas para tres energías cinéticas diferentes y cuatro posiciones iniciales dentro de la rendija. El ancho de la rendija se asigna directamente a los canales de detección de energía, lo que empeora la resolución. ${\displaystyle \rho =r_{0}-R_{\textrm {P}}}$

Trayectorias calculadas para cinco energías cinéticas diferentes y cinco ángulos iniciales. La dispersión angular inicial, que depende de la rendija y el ancho de apertura elegidos, empeora la resolución energética.

Cuando se aplican dos voltajes, y , a los hemisferios interno y externo, respectivamente, el potencial eléctrico en la región entre los dos electrodos se deduce de la ecuación de Laplace : ${\displaystyle V_{1}}$ ${\displaystyle V_{2}}$

${\displaystyle V(r)=-\left[{\frac {V_{2}-V_{1}}{R_{2}-R_{1}}}\right]\cdot {\frac {R_{1}R_{2}}{r}}+const.}$

El campo eléctrico, que apunta radialmente desde el centro de los hemisferios hacia afuera, tiene la forma familiar del movimiento planetario. ${\displaystyle 1/r^{2}}$

${\displaystyle |\mathbf {E} (r)|=-\left[{\frac {V_{2}-V_{1}}{R_{2}-R_{1}}}\right]\cdot {\frac {R_{1}R_{2}}{r^{2}}}}$

Los voltajes se establecen de tal manera que los electrones con energía cinética igual a la llamada energía de paso sigan una trayectoria circular de radio . La fuerza centrípeta a lo largo de la trayectoria está impuesta por el campo eléctrico . Con esto en mente, ${\displaystyle E_{k}}$ ${\displaystyle E_{\textrm {P}}}$ ${\displaystyle R_{\textrm {P}}={\tfrac {1}{2}}(R_{1}+R_{2})}$ ${\displaystyle -e\mathbf {E} (r)}$

${\displaystyle V(r)={\frac {E_{\textrm {P}}}{e}}{\frac {R_{\textrm {P}}}{r}}+const.}$

Es necesario calcular la diferencia de potencial entre los dos hemisferios.

${\displaystyle V_{1}-V_{2}={\frac {1}{e}}\left({\frac {R_{2}}{R_{1}}}-{\frac {R_{1}}{R_{2}}}\right)E_{\textrm {P}}}$.

Un único detector puntual situado en un radio situado al otro lado de los hemisferios registrará únicamente los electrones de una única energía cinética. Sin embargo, la detección puede paralelizarse debido a la dependencia casi lineal de los radios finales con respecto a la energía cinética. En el pasado, se utilizaban varios detectores de electrones discretos ( canaltrones ), pero ahora prevalecen las placas de microcanales con pantallas fosforescentes y la detección por cámara. ${\displaystyle R_{\textrm {P}}}$

En general, estas trayectorias se describen en coordenadas polares para el plano del círculo máximo para los electrones que inciden en un ángulo con respecto a la normal a la entrada, y para los radios iniciales para tener en cuenta los anchos finitos de apertura y rendija (normalmente de 0,1 a 5 mm): ^[4] ${\displaystyle r,\varphi }$ ${\displaystyle \alpha }$ ${\displaystyle r_{0}\equiv r(\varphi =0)}$

${\displaystyle r(\varphi )=r_{0}\,\left[{(1-c^{2})\cos \varphi -\tan \alpha \sin \varphi +c^{2}}\right]^{-1}}$

dónde

${\displaystyle c^{2}=R_{\textrm {P}}\left[{\tfrac {E_{\textrm {k}}}{E_{\textrm {P}}}}r_{0}\cos ^{2}\alpha -2\left(r_{0}-R_{\textrm {P}}\right)\right]^{-1}}$

Como se puede ver en las imágenes de las trayectorias de electrones calculadas, el ancho finito de la rendija se asigna directamente a los canales de detección de energía (confundiendo así la dispersión de energía real con el ancho del haz). La dispersión angular, si bien también empeora la resolución de energía, muestra cierto enfoque ya que las desviaciones negativas y positivas iguales se asignan al mismo punto final.

Distancia desde la trayectoria central a la salida de un analizador de energía de electrones hemisférico en función de la energía cinética del electrón, la posición inicial dentro de la rendija de 1 mm y el ángulo en el que entra en el campo radial después de pasar por la rendija. La dispersión es casi lineal en energía, lineal en posición inicial y cuadrática en ángulo. Las dos últimas se asignan a los canales de energía del detector, lo que estropea la resolución. Los datos se calcularon para R _p = 100 mm. Nótese que los órdenes de magnitud de las escalas son diferentes en los ejes verticales.

Cuando estas desviaciones de la trayectoria central se expresan en términos de los pequeños parámetros definidos como , , y teniendo en cuenta que en sí mismo es pequeño (del orden de 1°), el radio final de la trayectoria del electrón, , se puede expresar como ${\displaystyle \varepsilon ,\sigma }$ ${\displaystyle E_{k}=(1+\varepsilon )E_{\textrm {P}}}$ ${\displaystyle r_{0}=(1+\sigma )R_{\textrm {P}}}$ ${\displaystyle \alpha }$ ${\displaystyle r(\pi )}$

${\displaystyle r_{\pi }\approx R_{\textrm {P}}(1+2\varepsilon -\sigma -2\alpha ^{2}+2\varepsilon ^{2}-6\alpha ^{2}\varepsilon )}$.

Si los electrones de una energía fija entraran en el analizador a través de una rendija ancha, se visualizarían en el otro extremo del analizador como un punto de ancho. Si su dispersión angular máxima en la entrada es , se adquiere un ancho adicional de , y se extiende un único canal de energía en el lado del detector. Pero allí, este ancho adicional se interpreta como dispersión de energía, que es, en primer orden, . De ello se deduce que la resolución de energía instrumental, dada como una función del ancho de la rendija, , y el ángulo de incidencia máximo, , de los fotoelectrones entrantes, que a su vez depende del ancho de la apertura y la rendija, es ^[2] ${\displaystyle E_{k}}$ ${\displaystyle w}$ ${\displaystyle w}$ ${\displaystyle \alpha }$ ${\displaystyle 2R_{P}\,\alpha ^{2}}$ ${\displaystyle |\Delta r_{\pi }|_{\sigma ,\alpha }=w+2R_{P}\,\alpha ^{2}}$ ${\displaystyle |\Delta r_{\pi }|_{\varepsilon }=2R_{P}\,\Delta E/E_{P}}$ ${\displaystyle w}$ ${\displaystyle \alpha }$

${\displaystyle \Delta E=E_{\textrm {P}}\left({\frac {w}{2R_{\textrm {P}}}}+\alpha ^{2}\right)}$.

La resolución del analizador mejora con el aumento de . Sin embargo, los problemas técnicos relacionados con el tamaño del analizador limitan su valor real, y la mayoría de los analizadores lo tienen en el rango de 100-200 mm. Las energías de paso más bajas también mejoran la resolución, pero luego se reduce la probabilidad de transmisión de electrones y, en consecuencia, la relación señal-ruido se deteriora. Las lentes electrostáticas delante del analizador tienen dos propósitos principales: recogen y enfocan los fotoelectrones entrantes en la rendija de entrada del analizador, y desaceleran los electrones al rango de energías cinéticas alrededor de , para aumentar la resolución. ${\displaystyle R_{\textrm {P}}}$ ${\displaystyle E_{\textrm {P}}}$ ${\displaystyle E_{\textrm {P}}}$

En la adquisición de espectros en modo de barrido (o escaneo ), los voltajes de los dos hemisferios (y, por lo tanto, la energía de paso) se mantienen fijos; al mismo tiempo, los voltajes aplicados a las lentes electrostáticas se barren de tal manera que cada canal cuente electrones con la energía cinética seleccionada durante el tiempo seleccionado. Para reducir el tiempo de adquisición por espectro, se puede utilizar el llamado modo de instantánea (o fijo ). Este modo explota la relación entre la energía cinética de un fotoelectrón y su posición dentro del detector. Si el rango de energía del detector es lo suficientemente amplio y si la señal de fotoemisión recopilada de todos los canales es lo suficientemente fuerte, el espectro de fotoemisión se puede obtener en una sola toma de la imagen del detector.

Véase también

• Espectrometría de masas

Referencias

1. Roy, D.; Tremblay, D. (1990). "Diseño de espectrómetros electrónicos". Informes sobre el progreso en física . 53 (12): 1621–1674. Bibcode :1990RPPh...53.1621R. doi :10.1088/0034-4885/53/12/003. ISSN  0034-4885. S2CID  250872079.
2. Tusche, Christian; Chen, Ying-Jiun; Schneider, Claus M.; Kirschner, Jürgen (1 de noviembre de 2019). "Propiedades de formación de imágenes de analizadores de energía electrostática hemisféricos para microscopía de momento de alta resolución". Ultramicroscopía . 206 : 112815. doi : 10.1016/j.ultramic.2019.112815 . ISSN  0304-3991. PMID  31325896.
3. Hadjarab, F.; JL Erskine (1985). "Propiedades de imagen del analizador hemisférico aplicadas a la detección de energía multicanal". Revista de espectroscopia electrónica y fenómenos relacionados . 36 (3): 227. doi :10.1016/0368-2048(85)80021-9.
4. Análisis práctico de superficies: mediante espectroscopia de rayos X y de barrena. Briggs, D. (David), 1948-, Seah, MP Chichester: Wiley. 1983. ISBN 0-471-26279-X.OCLC 9556397  .{{cite book}}: CS1 maint: others (link)