En geometría , un octadecágono (u octacaidecágono [1] ) o 18-gono es un polígono de dieciocho lados . [2]
Un octadecágono regular tiene un símbolo de Schläfli {18} y puede construirse como un eneágono truncado cuasirregular , t{9}, que alterna dos tipos de aristas.
Como 18 = 2 × 3 2 , un octadecágono regular no se puede construir utilizando un compás y una regla . [3] Sin embargo, se puede construir utilizando neusis , o una trisección de ángulo con un tomahawk .

La siguiente construcción aproximada es muy similar a la del eneágono, ya que un octadecágono puede construirse como eneágono truncado. También es factible con el uso exclusivo de compás y regla.

El octadecágono regular tiene simetría Dih 18 , orden 36. Hay 5 simetrías diédricas de subgrupo: Dih 9 , (Dih 6 , Dih 3 ) y (Dih 2 Dih 1 ), y 6 simetrías de grupo cíclicas : (Z 18 , Z 9 ) , (Z 6 , Z 3 ) y (Z 2 , Z 1 ).
Estas 15 simetrías se pueden ver en 12 simetrías distintas en el octadecágono. John Conway las etiqueta con una letra y un orden de grupo. [4] La simetría completa de la forma regular es r36 y ninguna simetría se etiqueta como a1 . Las simetrías diedras se dividen dependiendo de si pasan por vértices ( d para diagonales) o aristas ( p para perpendiculares), e i cuando las líneas de reflexión pasan por aristas y vértices. Las simetrías cíclicas en la columna del medio se etiquetan como g para sus órdenes de giro centrales.
Cada simetría de subgrupo permite uno o más grados de libertad para formas irregulares. Solo el subgrupo g18 no tiene grados de libertad pero puede verse como aristas dirigidas .


Coxeter afirma que cada zonógono (un 2 m -gono cuyos lados opuestos son paralelos y de igual longitud) puede diseccionarse en m ( m -1)/2 paralelogramos. [6] En particular, esto es cierto para polígonos regulares con un número uniforme de lados, en cuyo caso los paralelogramos son todos rombos. Para el octadecágono regular , m = 9, y puede dividirse en 36: 4 conjuntos de 9 rombos. Esta descomposición se basa en una proyección de polígono de Petrie de un 9-cubo , con 36 de 4608 caras. La lista OEIS : A006245 enumera el número de soluciones como 112018190, incluidas rotaciones de hasta 18 pliegues y formas quirales en reflexión.
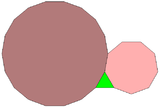
Un triángulo regular, un nonágono y un octadecágono pueden rodear completamente un punto en el plano, una de las 17 combinaciones diferentes de polígonos regulares con esta propiedad. [7] Sin embargo, este patrón no se puede extender a una teselación arquimediana del plano: debido a que el triángulo y el nonágono tienen ambos un número impar de lados, ninguno de ellos puede estar completamente rodeado por un anillo que alterne los otros dos tipos de polígono.
El octadecágono regular puede teselar el plano con huecos hexagonales cóncavos. Y otro teselado combina nonágonos y huecos octogonales. El primer teselado está relacionado con un teselado hexagonal truncado y el segundo con el teselado trihexagonal truncado .
Un octadecagrama es un polígono estrellado de 18 lados, representado por el símbolo {18/n}. Hay dos polígonos estrellados regulares : {18/5} y {18/7}, que utilizan los mismos puntos, pero conectan cada quinto o séptimo punto. También hay cinco compuestos: {18/2} se reduce a 2{9} o dos eneágonos , {18/3} se reduce a 3{6} o tres hexágonos , {18/4} y {18/8} se reducen a 2{9/2} y 2{9/4} o dos eneagramas , {18/6} se reduce a 6{3} o 6 triángulos equiláteros, y finalmente {18/9} se reduce a 9{2} como nueve dígonos .
Truncamientos más profundos del eneágono regular y de los eneagramas pueden producir formas de octadecagramas intermedios isogonales ( transitivos de vértice ) con vértices igualmente espaciados y dos longitudes de arista. Otros truncamientos forman recubrimientos dobles: t{9/8}={18/8}=2{9/4}, t{9/4}={18/4}=2{9/2}, t{9/2}={18/2}=2{9}. [8]
Un octadecágono oblicuo regular es el polígono de Petrie para una serie de politopos de dimensiones superiores, que se muestran en estas proyecciones ortogonales oblicuas de los planos de Coxeter :