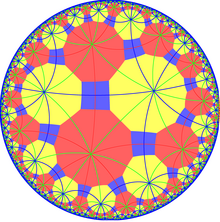
En geometría , el mosaico hexagonal truncado de orden 4 es un mosaico uniforme del plano hiperbólico . Tiene el símbolo de Schläfli t{6,4}. Una construcción secundaria tr{6,6} se denomina mosaico hexahexagonal truncado con dos colores de dodecágonos .
Hay dos construcciones uniformes de este teselado, la primera a partir del caleidoscopio [6,4] , y una simetría inferior al eliminar el último espejo, [6,4,1 + ], da [6,6], (*662).
El dual del mosaico representa los dominios fundamentales de la simetría orbifold (*662) . A partir de la simetría [6,6] (*662), hay 15 subgrupos de índice pequeños (12 únicos) por operadores de eliminación de espejos y alternancia . Los espejos se pueden eliminar si sus órdenes de ramificación son todos pares, y corta los órdenes de ramificación vecinos a la mitad. La eliminación de dos espejos deja un punto de giro de medio orden donde se encuentran los espejos eliminados. En estas imágenes, los dominios fundamentales están coloreados alternativamente en blanco y negro, y existen espejos en los límites entre los colores. El grupo de índice de subgrupo -8, [1 + ,6,1 + ,6,1 + ] (3333) es el subgrupo conmutador de [6,6].
Subgrupo más grande construido como [6,6 * ], eliminando los puntos de giro de (6*3), el índice 12 se convierte en (*333333).
La simetría se puede duplicar a simetría 642 agregando un espejo para bisecar el dominio fundamental.