
La óptica electrónica es un marco matemático para el cálculo de trayectorias de electrones en presencia de campos electromagnéticos . El término óptica se utiliza porque las lentes magnéticas y electrostáticas actúan sobre un haz de partículas cargadas de manera similar a como lo hacen las lentes ópticas sobre un haz de luz .
Los cálculos de óptica electrónica son cruciales para el diseño de microscopios electrónicos y aceleradores de partículas . En la aproximación paraxial , los cálculos de trayectoria se pueden realizar utilizando análisis de matriz de transferencia de rayos .
Los electrones son partículas cargadas ( cargas puntuales con masa en reposo ) con espín 1/2 (por lo tanto son fermiones ). Los electrones pueden acelerarse mediante campos eléctricos adecuados , adquiriendo así energía cinética . Dado un voltaje suficiente, el electrón puede acelerarse lo suficientemente rápido como para exhibir efectos relativistas mensurables . Según la dualidad onda-partícula , los electrones también pueden considerarse ondas de materia con propiedades como longitud de onda , fase y amplitud .
La analogía óptico-mecánica de Hamilton muestra que los rayos de electrones pueden modelarse utilizando conceptos y fórmulas matemáticas de rayos de luz. La fórmula de la trayectoria de partículas de electrones coincide con la fórmula de la óptica geométrica con un índice de refracción electrón-óptico adecuado. [1] : 745 Este índice de refracción funciona como las propiedades materiales del vidrio al alterar la dirección de propagación de los rayos. En la óptica de la luz, el índice de refracción cambia abruptamente en una superficie entre regiones de índice constante: los rayos se controlan con la forma de la interfaz. En la óptica electrónica, el índice varía a lo largo del espacio y está controlado por campos electromagnéticos creados fuera de las trayectorias de los electrones. [2]
Los electrones interactúan con los campos magnéticos según el segundo término de la fuerza de Lorentz: un producto vectorial entre el campo magnético y la velocidad del electrón. En un campo uniforme infinito, esto da como resultado un movimiento circular del electrón alrededor de la dirección del campo con un radio dado por:
donde r es el radio de la órbita, m es la masa de un electrón , es el componente de la velocidad del electrón perpendicular al campo, e es la carga del electrón y B es la magnitud del campo magnético aplicado. Los electrones que tienen un componente de velocidad paralelo al campo magnético avanzarán a lo largo de trayectorias helicoidales .
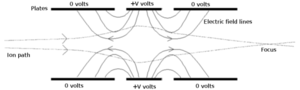
En el caso de un campo electrostático aplicado, un electrón se desviará hacia el gradiente positivo del campo. Cabe destacar que este cruce de líneas de campo electrostático significa que los electrones, a medida que se mueven a través de campos electrostáticos, cambian la magnitud de su velocidad, mientras que en los campos magnéticos, solo se modifica la dirección de la velocidad.
A la velocidad relativista del electrón, las ecuaciones ópticas geométricas del electrón se basan en un índice de refracción que incluye tanto la relación entre la velocidad del electrón y la luz como , el componente del potencial vectorial magnético a lo largo de la dirección del electrón: [1] : 754 donde , , y son la masa del electrón, la carga del electrón y la velocidad de la luz. El primer término está controlado por una lente electrostática mientras que el segundo por una lente magnética.
Aunque no es muy común, también es posible derivar efectos de estructuras magnéticas sobre partículas cargadas a partir de la ecuación de Dirac . [3]
Como los electrones pueden exhibir efectos no particulados (similares a ondas) como interferencia y difracción , un análisis completo de las trayectorias de los electrones debe ir más allá de la óptica geométrica. La propagación libre de electrones (en el vacío ) puede describirse con precisión como una onda de materia de De Broglie con una longitud de onda inversamente proporcional a su momento longitudinal ( posiblemente relativista ). Afortunadamente, mientras el campo electromagnético atravesado por el electrón cambie solo lentamente en comparación con esta longitud de onda (ver valores típicos en onda de materia#Aplicaciones de las ondas de materia ), se aplica la fórmula de difracción de Kirchhoff . [1] El carácter esencial de este enfoque es utilizar el trazado de rayos geométrico pero realizar un seguimiento de la fase de onda a lo largo de cada trayectoria para calcular la intensidad en el patrón de difracción.
Como resultado de la carga transportada por el electrón, los campos eléctricos, los campos magnéticos o el potencial interno medio electrostático de materiales delgados que interactúan débilmente pueden impartir un cambio de fase al frente de onda de un electrón. [4] Las membranas de nitruro de silicio moduladas por espesor y los dispositivos de cambio de fase programables han explotado estas propiedades para aplicar cambios de fase que varían espacialmente para controlar la intensidad espacial y la fase del campo lejano de la onda del electrón. Dispositivos como estos se han aplicado para dar forma arbitraria al frente de onda del electrón, corregir las aberraciones inherentes a los microscopios electrónicos , resolver el momento angular orbital de un electrón libre y medir el dicroísmo en la interacción entre electrones libres y materiales magnéticos o nanoestructuras plasmónicas. [5]
Los electrones interactúan fuertemente con la materia, ya que son sensibles no solo al núcleo, sino también a la nube de carga electrónica de la materia. Por lo tanto, los electrones necesitan vacío para propagarse a una distancia razonable, como sería deseable en un sistema óptico electrónico.
La penetración en el vacío está determinada por el camino libre medio , una medida de la probabilidad de colisión entre electrones y materia, cuyos valores aproximados pueden derivarse de las estadísticas de Poisson .
Programas comerciales
Software libre