
En geometría plana , un triángulo ABC contiene un triángulo que tiene un séptimo del área de ABC , que se forma de la siguiente manera: los lados de este triángulo se encuentran en las cevianas p, q, r donde
La prueba de la existencia del triángulo de área un séptimo se desprende de la construcción de seis líneas paralelas:
La sugerencia de Hugo Steinhaus es que el triángulo (central) con lados p,q,r se refleje en sus lados y vértices. [1] Estos seis triángulos adicionales cubren parcialmente a ABC y dejan seis triángulos adicionales que sobresalen fuera de ABC . Centrándose en el paralelismo de la construcción completa (ofrecida por Martin Gardner a través de la revista en línea de James Randi ), las congruencias por pares de las piezas sobresalientes y faltantes de ABC son evidentes. Como se ve en la solución gráfica, seis más el original es igual a todo el triángulo ABC . [2]
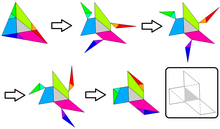
Una primera exposición de esta construcción geométrica y cálculo de área fue realizada por Robert Potts en 1859 en su libro de texto de geometría euclidiana. [3]
Según Cook y Wood (2004), este triángulo desconcertó a Richard Feynman en una conversación durante la cena; luego dan cuatro pruebas diferentes. [4]
Un resultado más general se conoce como teorema de Routh . Véase también el teorema de Marion Walter .