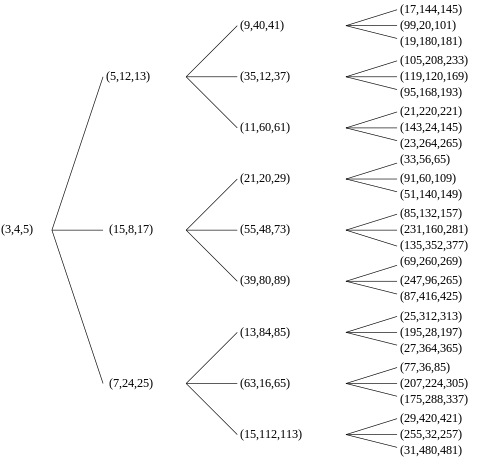
En matemáticas , un árbol de ternas pitagóricas primitivas es un árbol de datos en el que cada nodo se ramifica en tres nodos subsiguientes y el conjunto infinito de todos los nodos da todas (y únicas) ternas pitagóricas primitivas sin duplicación.
Una terna pitagórica es un conjunto de tres números enteros positivos a, b y c que tienen la propiedad de que pueden ser respectivamente los dos catetos y la hipotenusa de un triángulo rectángulo , satisfaciendo así la ecuación ; se dice que la terna es primitiva si y solo si el máximo común divisor de a, b y c es uno. Las ternas pitagóricas primitivas a, b y c también son coprimos por pares . El conjunto de todas las ternas pitagóricas primitivas tiene la estructura de un árbol con raíz , específicamente un árbol ternario , de manera natural. Esto fue descubierto por primera vez por B. Berggren en 1934. [1]
FJM Barning demostró [2] que cuando cualquiera de las tres matrices
Si se multiplica a la derecha por un vector columna cuyos componentes forman una terna pitagórica, el resultado es otro vector columna cuyos componentes son una terna pitagórica diferente. Si la terna inicial es primitiva, también lo es la resultante. Por lo tanto, cada terna pitagórica primitiva tiene tres "hijos". Todas las ternas pitagóricas primitivas descienden de esta manera de la terna (3, 4, 5), y ninguna terna primitiva aparece más de una vez. El resultado puede representarse gráficamente como un árbol ternario infinito con (3, 4, 5) en el nodo raíz (véase el árbol clásico a la derecha). Este árbol también apareció en los artículos de A. Hall en 1970 [3] y AR Kanga en 1990. [4] En 2008, VE Firstov demostró en general que solo existen tres árboles de tricotomía de este tipo y da explícitamente un árbol similar al de Berggren pero que comienza con el nodo inicial (4, 3, 5). [5]
Se puede demostrar inductivamente que el árbol contiene ternas pitagóricas primitivas y nada más, mostrando que a partir de una terna pitagórica primitiva, como la que está presente en el nodo inicial con (3, 4, 5), cada terna generada es a la vez pitagórica y primitiva.
Si cualquiera de las matrices anteriores, digamos A , se aplica a una tripleta ( a , b , c ) T que tiene la propiedad pitagórica a 2 + b 2 = c 2 para obtener una nueva tripleta ( d , e , f ) T = A ( a , b , c ) T , esta nueva tripleta también es pitagórica. Esto se puede ver escribiendo cada una de d , e y f como la suma de tres términos en a , b y c , elevando al cuadrado cada uno de ellos y sustituyendo c 2 = a 2 + b 2 para obtener f 2 = d 2 + e 2 . Esto es válido para B y C así como para A .
Las matrices A , B y C son todas unimodulares , es decir, tienen solo entradas enteras y sus determinantes son ±1. Por lo tanto, sus inversas también son unimodulares y, en particular, solo tienen entradas enteras. Entonces, si cualquiera de ellas, por ejemplo A , se aplica a una terna pitagórica primitiva ( a , b , c ) T para obtener otra terna ( d , e , f ) T , tenemos ( d , e , f ) T = A ( a , b , c ) T y, por lo tanto, ( a , b , c ) T = A −1 ( d , e , f ) T . Si cualquier factor primo fuera compartido por dos cualesquiera de (y, por lo tanto, los tres de) d , e y f , entonces, por esta última ecuación, ese primo también dividiría a cada uno de a , b y c . Por lo tanto, si a , b y c son, de hecho , primos entre sí, entonces d , e y f también deben ser primos entre sí. Esto es válido tanto para B y C como para A.
Para demostrar que el árbol contiene cada triple pitagórico primitivo, pero no más de una vez, basta con demostrar que para cualquier triple de este tipo hay exactamente un camino de vuelta a través del árbol hasta el nodo inicial (3, 4, 5). Esto se puede ver aplicando por turno cada una de las matrices inversas unimodulares A −1 , B −1 y C −1 a un triple pitagórico primitivo arbitrario ( d , e , f ), notando que por el razonamiento anterior se conservan la primitividad y la propiedad pitagórica, y notando que para cualquier triple mayor que (3, 4, 5) exactamente una de las matrices de transición inversa produce un nuevo triple con todas las entradas positivas (y una hipotenusa más pequeña). Por inducción, este nuevo triple válido conduce a su vez a exactamente un triple válido más pequeño, y así sucesivamente. Por la finitud del número de hipotenusas potenciales cada vez más pequeñas, finalmente se llega a (3, 4, 5). Esto demuestra que ( d , e , f ) de hecho ocurre en el árbol, ya que se puede llegar a él desde (3, 4, 5) invirtiendo los pasos; y ocurre únicamente porque había un solo camino desde ( d , e , f ) a (3, 4, 5).
La transformación que utiliza la matriz A , si se realiza repetidamente desde ( a , b , c ) = (3, 4, 5), conserva la característica b + 1 = c ; la matriz B conserva a – b = ±1 a partir de (3, 4, 5); y la matriz C conserva la característica a + 2 = c a partir de (3, 4, 5).
Una interpretación geométrica de este árbol implica los excírculos presentes en cada nodo. Los tres hijos de cualquier triángulo padre “heredan” sus inradios del padre: los radios de los excírculos del padre se convierten en los inradios de la siguiente generación. [6] : p.7 Por ejemplo, el padre (3, 4, 5) tiene radios de excírculos iguales a 2, 3 y 6. Estos son precisamente los inradios de los tres hijos (5, 12, 13), (15, 8, 17) y (21, 20, 29) respectivamente.
Si se aplica repetidamente A o C a partir de cualquier triple pitagórico utilizado como condición inicial, entonces la dinámica de cualquiera de a , b y c se puede expresar como la dinámica de x en
que se basa en la ecuación característica compartida de las matrices
Si B se aplica repetidamente, entonces la dinámica de cualquiera de a , b y c se puede expresar como la dinámica de x en
que se basa en la ecuación característica de B. [7 ]
Además, se puede hallar una infinidad de otras ecuaciones diferenciales univariadas de tercer orden multiplicando cualquiera de las tres matrices juntas un número arbitrario de veces en una secuencia arbitraria. Por ejemplo, la matriz D = CB se desplaza uno hacia afuera del árbol por dos nodos (a lo ancho y luego hacia abajo) en un solo paso; la ecuación característica de D proporciona el patrón para la dinámica de tercer orden de cualquiera de a , b o c en el árbol no exhaustivo formado por D .
Otro enfoque de la dinámica de este árbol [8] se basa en la fórmula estándar para generar todas las ternas pitagóricas primitivas:
con m > n > 0 y m y n coprimos y de paridad opuesta (es decir, no ambos impares). Los pares ( m , n ) se pueden iterar multiplicándolos previamente (expresados como un vector columna) por cualquiera de
cada uno de los cuales conserva las desigualdades, la coprimidad y la paridad opuesta. El árbol ternario resultante, que comienza en (2, 1) , contiene cada uno de esos pares ( m , n ) exactamente una vez, y cuando se convierte en triples ( a , b , c ) se vuelve idéntico al árbol descrito anteriormente.
Alternativamente, comience con ( m , n ) = (3, 1) para el nodo raíz. [9] Entonces las multiplicaciones de matrices preservarán las desigualdades y la coprimidad, y tanto m como n seguirán siendo impares. Las ternas pitagóricas primitivas correspondientes tendrán a = ( m 2 − n 2 ) / 2 , b = mn y c = ( m 2 + n 2 ) / 2 . Este árbol producirá las mismas ternas pitagóricas primitivas, aunque con a y b intercambiados.
Este enfoque se basa en la fórmula estándar para generar cualquier terna pitagórica primitiva a partir de una tangente de medio ángulo. Específicamente, se escribe t = n / m = b / ( a + c ) , donde t es la tangente de la mitad del ángulo interior opuesto al lado de longitud b . El nodo raíz del árbol es t = 1/2 , que es para la terna pitagórica primitiva (3, 4, 5) . Para cualquier nodo con valor t , sus tres hijos son 1 / (2 − t ) , 1 / (2 + t ) y t / (1 + 2 t ) . Para encontrar la terna pitagórica primitiva asociada con cualquier valor t , calcule (1 − t 2 , 2 t , 1 + t 2 ) y multiplique los tres valores por el mínimo común múltiplo de sus denominadores. (Alternativamente, escriba t = n / m como una fracción en términos más bajos y use las fórmulas de la sección anterior). Un nodo raíz que en cambio tenga el valor t = 1/3 dará el mismo árbol de ternas pitagóricas primitivas, aunque con los valores de a y b intercambiados.
.svg/1280px-Price's_tree_(classical_approach).svg.png)
Alternativamente, también se pueden utilizar tres matrices diferentes encontradas por Price. [6] Estas matrices A', B', C' y sus transformaciones lineales correspondientes se muestran a continuación.
Las tres transformaciones lineales de Price son
Los 3 hijos producidos por cada uno de los dos conjuntos de matrices no son los mismos, pero cada conjunto produce por separado todos los triples primitivos.
Por ejemplo, utilizando [5, 12, 13] como padre, obtenemos dos conjuntos de tres hijos:
![{\displaystyle {\overset {{A}'}{\mathop {\left[{\begin{matriz}2&1&-1\\-2&2&2\\-2&1&3\end{matriz}}\right]} }}\left[{\begin{matriz}a\\b\\c\end{matriz}}\right]=\left[{\begin{matriz}a_{1}\\b_{1}\\c_{1}\end{matriz}}\right],\quad {\text{ }}{\overset {{B}'}{\mathop {\left[{\begin{matriz}2&1&1\\2&-2&2\\2&-1&3\end{matriz}}\right]} }}\left[{\begin{matriz}a\\b\\c\\\end{matriz}}\right]=\left[{\begin{matriz}a_{2}\\b_{2}\\c_{2}\end{matriz}}\right],\quad {\text{ }}{\overset {{C}'}{\mathop {\left[{\begin{matriz}2&-1&1\\2&2&2\\2&1&3\\\end{matriz}}\right]} }}\left[{\begin{matriz}a\\b\\c\\\end{matriz}}\right]=\left[{\begin{matriz}a_{3}\\b_{3}\\c_{3}\end{matriz}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d879b7a73c5467ee7634d7b9ac8f317a00ebee52)
![{\displaystyle {\begin{aligned}&{\begin{matrix}+2a+bc=a_{1}\quad &-2a+2b+2c=b_{1}\quad &-2a+b+3c=c_{1}&\quad \to \left[{\text{ }}a_{1},{\text{ }}b_{1},{\text{ }}c_{1}\right]\end{matrix}}\\&{\begin{matrix}+2a+b+c=a_{2}\quad &+2a-2b+2c=b_{2}\quad &+2a-b+3c=c_{2}&\quad \to \left[{\text{ }}a_{2},{\text{ }}b_{2},{\text{ }}c_{2}\right]\end{matriz}}\\&{\begin{matriz}+2a-b+c=a_{3}\quad &+2a+2b+2c=b_{3}\quad &+2a+b+3c=c_{3}&\quad \to \left[{\text{ }}a_{3},{\text{ }}b_{3},{\text{ }}c_{3}\right]\end{matriz}}\\&\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4de34eeaf832afbd4829a0ee72a9ab6f785042ee)
![{\displaystyle {\begin{array}{ccc}&\left[5,12,13\right]&\\A&B&C\\\left[45,28,53\right]&\left[55,48,73\right]&\left[7,24,25\right]\end{array}}\quad \quad \quad \quad \quad \quad {\begin{array}{ccc}{}&\left[5,12,13\right]&{}\\A'&B'&C'\\\left[9,40,41\right]&\left[35,12,37\right]&\left[11,60,61\right]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0cd19d54783d1ad0b7b682d5fa047ee44379699)