En la historia de la física , " Sobre la reinterpretación teórica cuántica de las relaciones cinemáticas y mecánicas " ( alemán : Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen ), también conocido como el artículo Umdeutung ( reinterpretación ) , [1] [2] fue un gran avance . Artículo sobre mecánica cuántica escrito por Werner Heisenberg , que apareció en Zeitschrift für Physik en septiembre de 1925.
En el artículo, Heisenberg intentó explicar los niveles de energía de un oscilador anarmónico unidimensional , evitando las representaciones concretas pero no observables de las órbitas de los electrones mediante el uso de parámetros observables como las probabilidades de transición para los saltos cuánticos , lo que requirió el uso de dos índices correspondientes a los estados inicial y final. [3]
Matemáticamente, Heisenberg demostró la necesidad de operadores no conmutativos. Esta idea se convertiría más tarde en la base del principio de incertidumbre de Heisenberg .
Este artículo fue seguido por el artículo de Pascual Jordan y Max Born del mismo año, [4] y por el 'artículo de los tres hombres' ( en alemán : drei Männer Arbeit ) de Born, Heisenberg y Jordan en 1926. [5] [1] [6] Estos artículos sentaron las bases para la mecánica matricial que vendría a sustituir a la antigua teoría cuántica , dando lugar a la mecánica cuántica moderna. Heisenberg recibió el Premio Nobel de Física en 1932 por su trabajo en el desarrollo de la mecánica cuántica. [7]
Heisenberg tenía 23 años cuando trabajó en el artículo mientras se recuperaba de la fiebre del heno en la isla de Heligoland , y se carteó con Wolfgang Pauli sobre el tema. Cuando se le pidió su opinión sobre el manuscrito, Pauli respondió favorablemente, pero Heisenberg dijo que todavía estaba "muy inseguro al respecto". En julio de 1925, envió el manuscrito a Max Born para que lo revisara y decidiera si lo enviaba para su publicación. [8]
Cuando Born leyó el artículo, reconoció que la formulación podía transcribirse y extenderse al lenguaje sistemático de matrices. Born, con la ayuda de su asistente y antiguo alumno Pascual Jordan, comenzó inmediatamente a realizar la transcripción y extensión, y presentaron sus resultados para su publicación; su manuscrito fue recibido para su publicación sólo 60 días después del artículo de Heisenberg. [4] Un artículo de seguimiento de los tres autores que extendía la teoría a múltiples dimensiones fue presentado para su publicación antes de fin de año. [5]
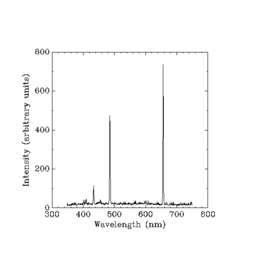
Heisenberg decidió basar su mecánica cuántica "exclusivamente en relaciones entre cantidades que en principio son observables". [9] Observó que no se podía utilizar ningún enunciado sobre cuestiones como "la posición y el período de revolución del electrón". [10] Más bien, para hacer un verdadero progreso en la comprensión de la radiación del caso más simple, la radiación de los átomos de hidrógeno excitados, sólo se contaba con mediciones de las frecuencias e intensidades del espectro de líneas brillantes del hidrógeno con las que trabajar.

En física clásica , la intensidad de cada frecuencia de luz producida en un sistema radiante es igual al cuadrado de la amplitud de la radiación a esa frecuencia, por lo que la atención se centró en las amplitudes. Las ecuaciones clásicas que Heisenberg esperaba utilizar para formar ecuaciones teóricas cuánticas darían primero las amplitudes, y en física clásica se podrían calcular las intensidades simplemente elevando al cuadrado las amplitudes. Pero Heisenberg vio que "la suposición más simple y natural sería" [11] seguir el ejemplo proporcionado por el trabajo reciente en el cálculo de la dispersión de la luz realizado por Hans Kramers . [12] El trabajo que había realizado ayudando a Kramers el año anterior [13] ahora le dio una pista importante sobre cómo modelar lo que le sucedía al gas hidrógeno excitado cuando irradiaba luz y lo que sucedía cuando la radiación entrante de una frecuencia excitaba átomos en un medio dispersivo y luego la energía entregada por la luz entrante se reirradiaba, a veces a la frecuencia original, pero a menudo a dos frecuencias más bajas cuya suma era igual a la frecuencia original. Según su modelo, un electrón que hubiera sido impulsado a un estado de mayor energía al aceptar la energía de un fotón entrante podría regresar en un solo paso a su posición de equilibrio, volviendo a irradiar un fotón de la misma frecuencia, o podría regresar en más de un paso, irradiando un fotón por cada paso en su regreso a su estado de equilibrio. Debido a la forma en que se cancelan los factores al derivar la nueva ecuación basada en estas consideraciones, el resultado resulta relativamente simple.
También se incluyó en el manuscrito el conmutador de Heisenberg , su ley de multiplicación necesaria para describir ciertas propiedades de los átomos, por la cual el producto de dos cantidades físicas no conmutaba . Por lo tanto, PQ diferiría de QP donde, por ejemplo, P era el momento de un electrón y Q su posición. Paul Dirac , que había recibido una copia de prueba en agosto de 1925, se dio cuenta de que la ley conmutativa no había sido completamente desarrollada y produjo una formulación algebraica para expresar los mismos resultados en una forma más lógica. [14]
Mediante una intensa serie de analogías matemáticas que algunos físicos han calificado de «mágicas», Heisenberg escribió una ecuación que es el análogo mecánico cuántico del cálculo clásico de intensidades. La ecuación que aparece a continuación aparece en el artículo. [15] [16] Su forma general es la siguiente:
Este formato general indica que se debe calcular un término C sumando todos los productos de un grupo de términos A por un grupo relacionado de términos B. Potencialmente habrá una serie infinita de términos A y sus términos B correspondientes . Cada una de estas multiplicaciones tiene como factores dos mediciones que pertenecen a transiciones descendentes secuenciales entre estados de energía de un electrón. Este tipo de regla diferencia la mecánica matricial del tipo de física familiar en la vida cotidiana porque los valores importantes son dónde (en qué estado de energía u "orbital") comienza el electrón y en qué estado de energía termina, no lo que está haciendo el electrón mientras está en uno u otro estado.
Si A y B hacen referencia a listas de frecuencias, por ejemplo, el cálculo se realiza de la siguiente manera:
Multiplica la frecuencia de un cambio de energía del estado n al estado n − a por la frecuencia de un cambio de energía del estado n − a al estado n − b y a eso súmale el producto que se obtiene al multiplicar la frecuencia de un cambio de energía del estado n − a al estado n − b por la frecuencia de un cambio de energía del estado n − b al estado n − c , y así sucesivamente. Simbólicamente, esto es:
(Según la convención utilizada, n − a representa un estado de energía mayor que n , por lo que una transición de n a n − a indicaría que un electrón ha aceptado energía de un fotón entrante y ha subido a un orbital superior, mientras que una transición de n − a a n representaría un electrón que cae a un orbital inferior y emite un fotón).
Sería fácil realizar cada paso individual de este proceso para una determinada cantidad medida. Por ejemplo, la fórmula enmarcada al principio de este artículo proporciona cada longitud de onda necesaria en secuencia. Los valores calculados podrían rellenarse fácilmente en una cuadrícula como se describe a continuación. Sin embargo, dado que la serie es infinita, nadie podría realizar todo el conjunto de cálculos.
Heisenberg ideó originalmente esta ecuación para poder multiplicar dos medidas del mismo tipo (amplitudes), de modo que no importara en qué orden se multiplicaran. Sin embargo, Heisenberg se dio cuenta de que si intentaba utilizar el mismo esquema para multiplicar dos variables, como el momento, p , y el desplazamiento, q , "surge una dificultad significativa". [17] Resulta que multiplicar una matriz de p por una matriz de q da un resultado diferente de multiplicar una matriz de q por una matriz de p . Solo había una pequeña diferencia, pero esa diferencia nunca podía reducirse por debajo de un cierto límite, y ese límite involucraba la constante de Planck , h . Más sobre eso más adelante. A continuación se muestra una muestra muy breve de cómo serían los cálculos, colocados en cuadrículas que se llaman matrices. El maestro de Heisenberg vio casi inmediatamente que su trabajo debería expresarse en un formato matricial porque los matemáticos ya estaban familiarizados con la forma de hacer cálculos que involucraban matrices de una manera eficiente. (Dado que Heisenberg estaba interesado en la radiación de fotones, las ilustraciones se darán en términos de electrones que van desde un nivel de energía más alto a un nivel más bajo, por ejemplo, n ← n − 1 , en lugar de ir desde un nivel más bajo a un nivel más alto, por ejemplo, n → n − 1 .) (ecuación para las variables conjugadas momento y posición)
Matriz de p
Matriz de q
La matriz para el producto de las dos matrices anteriores, tal como se especifica en la ecuación pertinente del documento de Umdeutung , es
dónde
y así sucesivamente.
Si se invirtieran las matrices, resultarían los siguientes valores
y así sucesivamente.

Werner Heisenberg utilizó la idea de que, puesto que la física clásica es correcta cuando se aplica a fenómenos del mundo de cosas más grandes que los átomos y las moléculas, debe ser considerada como un caso especial de un modelo teórico cuántico más inclusivo. Por lo tanto, esperaba poder modificar la física cuántica de tal manera que cuando los parámetros estuvieran en la escala de los objetos cotidianos se parecería a la física clásica, pero cuando los parámetros se redujeran a la escala atómica, las discontinuidades observadas en cosas como las frecuencias ampliamente espaciadas del espectro de líneas brillantes del hidrógeno visible volverían a aparecer.
Lo que más quería entender la gente de la época sobre la radiación del hidrógeno era cómo predecir o explicar las intensidades de las líneas de su espectro. Aunque Heisenberg no lo sabía en aquel momento, el formato general que ideó para expresar su nueva forma de trabajar con cálculos teóricos cuánticos puede servir como receta para dos matrices y cómo multiplicarlas. [18]
El artículo de Umdeutung no menciona matrices. El gran avance de Heisenberg fue el "esquema que, en principio, era capaz de determinar de manera única las cualidades físicas relevantes (frecuencias de transición y amplitudes)" [19] de la radiación de hidrógeno.
Después de que Heisenberg escribiera el artículo sobre la definición de matrices , se lo entregó a uno de sus colegas de mayor antigüedad para que hiciera las correcciones necesarias y se fue de vacaciones. Max Born se quedó perplejo con las ecuaciones y las ecuaciones no conmutativas que Heisenberg había encontrado problemáticas y perturbadoras. Después de varios días se dio cuenta de que estas ecuaciones equivalían a instrucciones para escribir matrices. [20]
Al considerar... ejemplos... [Heisenberg] encontró esta regla... Esto fue en el verano de 1925. Heisenberg... se despidió... y me entregó su artículo para que lo publicara... La regla de multiplicación de Heisenberg no me dejó en paz, y después de una semana de intensa reflexión y ensayo, de repente recordé una teoría algebraica... Tales matrices cuadráticas son bastante familiares para los matemáticos y se llaman matrices, en asociación con una regla de multiplicación definida. Apliqué esta regla a la condición cuántica de Heisenberg y descubrí que concordaba con los elementos diagonales. Era fácil adivinar cuáles debían ser los elementos restantes, es decir, nulos; e inmediatamente apareció ante mí la extraña fórmula
El símbolo Q es la matriz del desplazamiento, P es la matriz del momento, i representa la raíz cuadrada de menos uno y h es la constante de Planck. [21] Born y algunos colegas se pusieron a trabajar en la tarea de resolver todo en forma matricial antes de que Heisenberg regresara de su tiempo libre y, en pocos meses, la nueva mecánica cuántica en forma matricial formó la base de otro artículo. Esta relación se conoce ahora como el principio de incertidumbre de Heisenberg .
Cuando se mencionan magnitudes como la posición y el momento en el contexto de la mecánica matricial de Heisenberg, una afirmación como pq ≠ qp no se refiere a un único valor de p y a un único valor de q, sino a una matriz (una cuadrícula de valores dispuestos de una manera definida) de valores de posición y una matriz de valores de momento. Por lo tanto, multiplicar p por q o q por p en realidad se refiere a la multiplicación matricial de las dos matrices. Cuando se multiplican dos matrices, la respuesta es una tercera matriz.
Paul Dirac decidió que la esencia del trabajo de Heisenberg residía en la misma característica que Heisenberg había considerado problemática originalmente: el hecho de la no conmutatividad, como la que existe entre la multiplicación de una matriz de momento por una matriz de desplazamiento y la multiplicación de una matriz de desplazamiento por una matriz de momento. Esa idea llevó a Dirac por nuevas y productivas direcciones. [22]