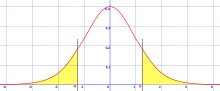
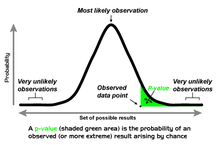
En las pruebas de significancia estadística , una prueba de una cola y una prueba de dos colas son formas alternativas de calcular la significancia estadística de un parámetro inferido de un conjunto de datos, en términos de una estadística de prueba . Una prueba de dos colas es apropiada si el valor estimado es mayor o menor que un cierto rango de valores, por ejemplo, si un examinado puede puntuar por encima o por debajo de un rango específico de puntuaciones. Este método se utiliza para pruebas de hipótesis nulas y si el valor estimado existe en las áreas críticas, la hipótesis alternativa se acepta sobre la hipótesis nula. Una prueba de una cola es apropiada si el valor estimado puede alejarse del valor de referencia solo en una dirección, izquierda o derecha, pero no en ambas. Un ejemplo puede ser si una máquina produce más del uno por ciento de productos defectuosos. En esta situación, si el valor estimado existe en una de las áreas críticas unilaterales, dependiendo de la dirección de interés (mayor que o menor que), la hipótesis alternativa se acepta sobre la hipótesis nula. Los nombres alternativos son pruebas unilaterales y bilaterales ; Se utiliza el término "cola" porque las porciones extremas de las distribuciones, donde las observaciones llevan al rechazo de la hipótesis nula, son pequeñas y a menudo "se reducen" hacia cero, como en la distribución normal , coloreada en amarillo, o la "curva de campana", ilustrada a la derecha y coloreada en verde.
Las pruebas de una cola se utilizan para distribuciones asimétricas que tienen una sola cola, como la distribución de chi-cuadrado , que son comunes para medir la bondad de ajuste , o para un lado de una distribución que tiene dos colas, como la distribución normal , que es común para estimar la ubicación; esto corresponde a especificar una dirección. Las pruebas de dos colas solo son aplicables cuando hay dos colas, como en la distribución normal, y corresponden a considerar que cualquiera de las direcciones es significativa. [1] [2]
En el enfoque de Ronald Fisher , la hipótesis nula H 0 será rechazada cuando el valor p del estadístico de prueba sea suficientemente extremo (en comparación con la distribución de muestreo del estadístico de prueba ) y, por lo tanto, se juzgue improbable que sea el resultado del azar. Esto generalmente se hace comparando el valor p resultante con el nivel de significancia especificado, denotado por , al calcular la significancia estadística de un parámetro . En una prueba de una cola, "extremo" se decide de antemano como "suficientemente pequeño" o "suficientemente grande"; los valores en la otra dirección se consideran no significativos. Se puede informar que la probabilidad de la cola izquierda o derecha es el valor p de una cola, que en última instancia corresponde a la dirección en la que el estadístico de prueba se desvía de H 0. [3] En una prueba de dos colas, "extremo" significa "suficientemente pequeño o suficientemente grande", y los valores en cualquier dirección se consideran significativos. [4] Para una estadística de prueba dada, hay una sola prueba de dos colas y dos pruebas de una cola, una para cada dirección. Cuando se proporciona un nivel de significancia , las regiones críticas existirían en los dos extremos de la distribución con un área de cada uno para una prueba de dos colas. Alternativamente, la región crítica existiría únicamente en el extremo de una sola cola con un área de para una prueba de una cola. Para un nivel de significancia dado en una prueba de dos colas para una estadística de prueba, las pruebas de una cola correspondientes para la misma estadística de prueba se considerarán dos veces más significativas (la mitad del valor p ) si los datos están en la dirección especificada por la prueba, o no significativas en absoluto ( valor p por encima ) si los datos están en la dirección opuesta a la región crítica especificada por la prueba.
Por ejemplo, si se lanza una moneda al aire, comprobar si está sesgada hacia cara es una prueba de una cola, y obtener datos de "todas las caras" se consideraría altamente significativo, mientras que obtener datos de "todas las cruces" no sería significativo en absoluto ( p = 1). Por el contrario, comprobar si está sesgada en cualquier dirección es una prueba de dos colas, y tanto "todas las caras" como "todas las cruces" se considerarían datos altamente significativos. En las pruebas médicas, aunque uno generalmente está interesado en si un tratamiento da como resultado resultados que son mejores que el azar, lo que sugiere una prueba de una cola; un resultado peor también es interesante para el campo científico, por lo tanto, uno debería usar una prueba de dos colas que corresponda en cambio a comprobar si el tratamiento da como resultado resultados que son diferentes del azar, ya sea mejores o peores. [5] En el experimento de la dama arquetípica que degustaba té , Fisher probó si la dama en cuestión era mejor que el azar para distinguir dos tipos de preparación de té, no si su capacidad era diferente del azar, y por lo tanto utilizó una prueba de una cola.
En el lanzamiento de una moneda, la hipótesis nula es una secuencia de ensayos de Bernoulli con probabilidad de 0,5, que produce una variable aleatoria X que es 1 para cara y 0 para cruz, y una estadística de prueba común es la media de la muestra (del número de caras). Si se prueba si la moneda está sesgada hacia cara, se utilizaría una prueba de una cola: solo un gran número de caras sería significativo. En ese caso, un conjunto de datos de cinco caras (HHHHH), con media de muestra de 1, tiene una probabilidad de ocurrir, (5 lanzamientos consecutivos con 2 resultados - ((1/2)^5 =1/32). Esto tendría y sería significativo (rechazando la hipótesis nula) si la prueba se analizara a un nivel de significancia de (el nivel de significancia correspondiente al límite de corte). Sin embargo, si se prueba si la moneda está sesgada hacia cara o cruz, se usaría una prueba de dos colas, y un conjunto de datos de cinco caras (media de muestra 1) es tan extremo como un conjunto de datos de cinco cruces (media de muestra 0). Como resultado, el valor p sería y esto no sería significativo (sin rechazar la hipótesis nula) si la prueba se analizara a un nivel de significancia de .

El valor p fue introducido por Karl Pearson [6] en la prueba de chi-cuadrado de Pearson , donde definió P (notación original) como la probabilidad de que la estadística esté en o por encima de un nivel dado. Esta es una definición de una cola, y la distribución de chi-cuadrado es asimétrica, solo asume valores positivos o cero, y tiene solo una cola, la superior. Mide la bondad de ajuste de los datos con una distribución teórica, donde cero corresponde a un acuerdo exacto con la distribución teórica; el valor p mide la probabilidad de que el ajuste sea tan malo o peor.

La distinción entre pruebas de una cola y de dos colas fue popularizada por Ronald Fisher en el influyente libro Statistical Methods for Research Workers [7] , donde la aplicó especialmente a la distribución normal , que es una distribución simétrica con dos colas iguales. La distribución normal es una medida común de ubicación, en lugar de bondad de ajuste, y tiene dos colas, que corresponden a la estimación de la ubicación por encima o por debajo de la ubicación teórica (por ejemplo, la media de la muestra comparada con la media teórica). En el caso de una distribución simétrica como la distribución normal, el valor p de una cola es exactamente la mitad del valor p de dos colas : [7]
A veces se produce cierta confusión por el hecho de que en algunos casos deseamos saber la probabilidad de que la desviación, que se sabe que es positiva, exceda un valor observado, mientras que en otros casos la probabilidad requerida es que una desviación, que con igual frecuencia es positiva y negativa, exceda un valor observado; la última probabilidad es siempre la mitad de la primera.
Fisher enfatizó la importancia de medir la cola –el valor observado de la estadística de prueba y todos los más extremos– en lugar de simplemente la probabilidad del resultado específico en sí, en su The Design of Experiments (1935). [8] Explica esto porque un conjunto específico de datos puede ser improbable (en la hipótesis nula), pero resultados más extremos probables, por lo que vistos desde esta perspectiva, los datos específicos pero no extremadamente improbables no deberían considerarse significativos.
Si la estadística de prueba sigue una distribución t de Student en la hipótesis nula (lo cual es común cuando la variable subyacente sigue una distribución normal con un factor de escala desconocido), entonces la prueba se denomina prueba t de una o dos colas . Si la prueba se realiza utilizando la media y la varianza de la población real, en lugar de una estimación de una muestra, se denominaría prueba Z de una o dos colas .
Las tablas estadísticas para t y para Z proporcionan valores críticos para pruebas de una y dos colas. Es decir, proporcionan los valores críticos que excluyen una región entera en uno u otro extremo de la distribución de muestreo, así como los valores críticos que excluyen las regiones (de la mitad del tamaño) en ambos extremos de la distribución de muestreo.
{{cite book}}: Mantenimiento de CS1: otros ( enlace )