La geomorfometría , o geomorfometría ( griego antiguo : γῆ , romanizado : gê , lit. 'tierra' + griego antiguo : μορφή , romanizado : morphḗ , lit. 'forma, figura' + griego antiguo : μέτρον , romanizado : métron , lit. 'medida'), es la ciencia y la práctica de medir las características del terreno , la forma de la superficie de la Tierra y los efectos de esta forma de la superficie en la geografía humana y natural. [1] Reúne varias técnicas matemáticas, estadísticas y de procesamiento de imágenes que se pueden utilizar para cuantificar aspectos morfológicos, hidrológicos, ecológicos y otros de una superficie terrestre. Los sinónimos comunes de geomorfometría son análisis geomorfológico (después de geomorfología ), morfometría del terreno , análisis del terreno y análisis de la superficie terrestre . La geomorfometría es la disciplina basada en las medidas computacionales de la geometría , topografía y forma de los horizontes de la Tierra y su cambio temporal . [2] Este es un componente importante de los sistemas de información geográfica (SIG) y otras herramientas de software para el análisis espacial.
En términos simples, la geomorfometría tiene como objetivo extraer parámetros de la superficie (terrestre) (morfométricos, hidrológicos, climáticos, etc.) y objetos (cuencas hidrográficas, redes de arroyos, accidentes geográficos, etc.) utilizando un modelo digital de superficie terrestre de entrada (también conocido como modelo digital de elevación , DEM) y software de parametrización. [3] Los parámetros y objetos de superficie extraídos se pueden utilizar, por ejemplo, para mejorar el mapeo y modelado de suelos, vegetación, uso de la tierra, características geomorfológicas y geológicas y similares.
Con el rápido aumento de las fuentes de DEM en la actualidad (y principalmente debido a la Shuttle Radar Topography Mission y los proyectos basados en LIDAR ), la extracción de parámetros de la superficie terrestre se está volviendo cada vez más atractiva para numerosos campos que van desde la agricultura de precisión , el modelado de suelos y paisajes, las aplicaciones climáticas e hidrológicas hasta la planificación urbana, la educación y la investigación espacial. La topografía de casi toda la Tierra ha sido muestreada o escaneada hoy en día, de modo que los DEM están disponibles con resoluciones de 100 m o mejores a escala global. Hoy en día, los parámetros de la superficie terrestre se utilizan con éxito tanto para el modelado estocástico como para el basado en procesos, siendo el único problema restante el nivel de detalle y la precisión vertical del DEM.
Aunque la geomorfometría comenzó con las ideas de Brisson (1808) y Gauss (1827), el campo no evolucionó mucho hasta el desarrollo de los conjuntos de datos SIG y DEM en la década de 1970. [4]
La geomorfología (que se centra en los procesos que modifican la superficie terrestre) tiene una larga historia como concepto y área de estudio, siendo la geomorfometría una de las disciplinas relacionadas más antiguas. [5] La geomática es una subdisciplina de evolución más reciente, y aún más reciente es el concepto de geomorfometría. Esto solo se ha desarrollado recientemente desde la disponibilidad de software de sistema de información geográfica (SIG) más flexible y capaz, así como un modelo digital de elevación (DEM) de mayor resolución. [6] Es una respuesta al desarrollo de esta tecnología SIG para recopilar y procesar datos DEM (por ejemplo, teledetección , el programa Landsat y fotogrametría ). Las aplicaciones recientes proceden con la integración de la geomorfometría con variables de análisis de imágenes digitales obtenidas por teledetección aérea y satelital . [7] A medida que la red irregular triangulada (TIN) surgió como un modelo alternativo para representar la superficie del terreno, se desarrollaron algoritmos correspondientes para derivar mediciones de ella.
Se pueden derivar varias mediciones básicas de la superficie del terreno, generalmente aplicando las técnicas del cálculo vectorial . Dicho esto, los algoritmos que se utilizan normalmente en SIG y otros programas utilizan cálculos aproximados que producen resultados similares en mucho menos tiempo con conjuntos de datos discretos que los métodos de función continua pura. [8] Se han desarrollado muchas estrategias y algoritmos, cada uno con ventajas y desventajas. [9] [10] [11]

La normal de la superficie en cualquier punto de la superficie del terreno es un rayo vectorial perpendicular a la superficie. El gradiente de la superficie ( ) es el rayo vectorial tangente a la superficie, en la dirección de la pendiente descendente más pronunciada.
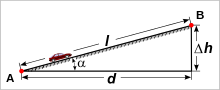
La pendiente mide la inclinación del terreno en cualquier punto de la superficie, desviándose de una superficie horizontal. En principio, es el ángulo entre el vector de pendiente y el plano horizontal, expresado como una medida angular α (común en aplicaciones científicas) o como la relación , comúnmente expresada como un porcentaje, tal que p = tan α . Esta última se utiliza con frecuencia en aplicaciones de ingeniería como la construcción de carreteras y ferrocarriles.
Para obtener la pendiente de un modelo de elevación digital ráster es necesario calcular una aproximación discreta de la derivada de la superficie en función de la elevación de una celda y las de las celdas que la rodean, y se han desarrollado varios métodos. [12] Por ejemplo, el método de Horne, implementado en ArcGIS , utiliza la elevación de una celda y sus ocho vecinos inmediatos, espaciados por el tamaño de la celda o la resolución r : [13] [14]
Las derivadas parciales se aproximan luego como promedios ponderados de las diferencias entre los lados opuestos:
Luego se calcula la pendiente (en porcentaje) utilizando el teorema de Pitágoras :
La segunda derivada de la superficie (es decir, la curvatura) se puede obtener utilizando cálculos análogos similares.
La orientación del terreno en cualquier punto de la superficie es la dirección a la que se enfrenta la pendiente, o la dirección cardinal de la pendiente descendente más pronunciada. En principio, es la proyección del gradiente sobre la pendiente horizontal. En la práctica, utilizando un modelo de elevación digital ráster , se aproxima utilizando uno de los mismos métodos de aproximación de derivadas parciales desarrollados para la pendiente. [12] Luego, la orientación se calcula como: [15]
Esto produce un rumbo en sentido antihorario, con 0° al este.

Otro producto útil derivado de la superficie del terreno es una imagen de relieve sombreado , que aproxima el grado de iluminación de la superficie a partir de una fuente de luz que proviene de una dirección dada. En principio, el grado de iluminación es inversamente proporcional al ángulo entre el vector normal de la superficie y el vector de iluminación; cuanto mayor sea el ángulo entre los vectores, más oscuro será ese punto en la superficie. En la práctica, se puede calcular a partir de la pendiente α y el aspecto β , en comparación con una altitud φ y un acimut θ correspondientes de la fuente de luz: [16]
La imagen resultante rara vez es útil para fines analíticos, pero se utiliza más comúnmente como una visualización intuitiva de la superficie del terreno porque parece un modelo tridimensional iluminado de la superficie.
Las características naturales del terreno, como las montañas y los cañones, a menudo se pueden reconocer como patrones de elevación y sus propiedades derivadas. Los patrones más básicos incluyen lugares donde el terreno cambia abruptamente, como picos (máximos de elevación local), fosos (mínimos de elevación local), crestas (máximos lineales), canales (mínimos lineales) y pasos (las intersecciones de crestas y canales).
Debido a las limitaciones de resolución , orientación de ejes y definiciones de objetos, los datos espaciales derivados pueden producir significado con observación subjetiva o parametrización , o alternativamente procesarse como datos difusos para manejar los errores variables que contribuyen de manera más cuantitativa – por ejemplo, como una probabilidad general del 70% de que un punto represente el pico de una montaña dados los datos disponibles, en lugar de una suposición fundamentada para lidiar con la incertidumbre. [17]
En muchas aplicaciones, resulta útil saber cuánto varía la superficie en cada área local. Por ejemplo, puede ser necesario distinguir entre áreas montañosas y altas mesetas, ambas de gran altitud pero con diferentes grados de "rugosidad". El relieve local de una celda es una medida de esta variabilidad en el entorno circundante (normalmente las celdas dentro de un radio determinado), para lo cual se han utilizado varias medidas, incluidas estadísticas de resumen simples como el rango total de valores en el entorno, un rango intercuartil o la desviación estándar. También se han desarrollado fórmulas más complejas para capturar variaciones más sutiles. [18]
El análisis cuantitativo de superficies mediante geomorfometría proporciona diversas herramientas para científicos y administradores interesados en la gestión de tierras. [19] Las áreas de aplicación incluyen:

En muchas situaciones, el terreno puede afectar profundamente los entornos locales, especialmente en climas semiáridos y áreas montañosas. Esto incluye efectos bien conocidos como la zonificación altitudinal y el efecto de pendiente . Esto puede convertirlo en un factor significativo en el modelado y mapeo de microclimas , distribución de vegetación , hábitat de vida silvestre y agricultura de precisión .
Debido a que el agua fluye cuesta abajo, las derivadas de la superficie del terreno pueden predecir el flujo superficial de los arroyos. Esto se puede utilizar para construir redes de arroyos, delinear cuencas de drenaje y calcular la acumulación total de flujo.
Las montañas y otros accidentes geográficos pueden bloquear la visibilidad entre ubicaciones en lados opuestos. Predecir este efecto es una herramienta valiosa para aplicaciones tan variadas como las tácticas militares y la ubicación de estaciones base . Las herramientas comunes en el software de análisis de terreno incluyen el cálculo de la visibilidad de la línea de visión entre dos puntos y la generación de una cuenca visual , la región de todos los puntos visibles desde un único punto. [20]

Muchos proyectos de construcción requieren una modificación importante de la superficie del terreno, que incluye tanto la eliminación como la adición de material. Al modelar la superficie actual y la diseñada, los ingenieros pueden calcular el volumen de cortes y rellenos, y predecir posibles problemas como la estabilidad de la pendiente y el potencial de erosión.
Como una rama relativamente nueva y desconocida de los SIG, el tema de la geomorfometría tiene pocas figuras pioneras "famosas", como es el caso de otros campos como la hidrología ( Robert Horton ) o la geomorfología ( GK Gilbert [21] ). En el pasado, la geomorfometría se ha utilizado en muchos estudios (incluidos algunos artículos de geomorfología de alto perfil de académicos como Evans, Leopold y Wolman). Aún así, solo recientemente los profesionales de los SIG han comenzado a integrarla en su trabajo. [22] [23] No obstante, cada vez más investigadores como Andy Turner y Joseph Wood la utilizan.
Las grandes instituciones están desarrollando cada vez más aplicaciones geomorfométricas basadas en SIG. Un ejemplo es la creación de un paquete de software basado en Java para morfometría en asociación con la Universidad de Leeds .
Las instituciones académicas dedican cada vez más recursos a la formación en geomorfometría y a cursos específicos, aunque estos todavía se limitan a unas pocas universidades y centros de formación. Los más accesibles en la actualidad incluyen una biblioteca de recursos de geomorfometría en línea en colaboración con la Universidad de Leeds y conferencias y prácticas impartidas como parte de módulos SIG más amplios, los más completos en la actualidad se ofrecen en la Universidad de Columbia Británica (supervisada por Brian Klinkenberg) y en la Universidad de Dalhousie .
El siguiente software informático tiene módulos o extensiones de análisis de terreno especializados (enumerados en orden alfabético):