En matemáticas , el plano complejo es el plano formado por los números complejos , con un sistema de coordenadas cartesianas tal que el eje horizontal x , llamado eje real , está formado por los números reales , y el eje vertical y , llamado eje imaginario , está formado por los números imaginarios .
El plano complejo permite una interpretación geométrica de los números complejos. En la suma , se suman como vectores . La multiplicación de dos números complejos se puede expresar más fácilmente en coordenadas polares : la magnitud o módulo del producto es el producto de los dos valores absolutos , o módulos, y el ángulo o argumento del producto es la suma de los dos ángulos, o argumentos. En particular, la multiplicación por un número complejo de módulo 1 actúa como una rotación.
El plano complejo a veces se denomina plano de Argand o plano de Gauss .
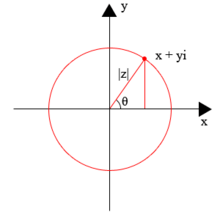
En el análisis complejo , los números complejos se representan habitualmente con el símbolo z , que puede separarse en sus partes real ( x ) e imaginaria ( y ):
Por ejemplo: z = 4 + 5 i , donde x e y son números reales e i es la unidad imaginaria . En esta notación habitual, el número complejo z corresponde al punto ( x , y ) en el plano cartesiano ; el punto ( x , y ) también se puede representar en coordenadas polares con:
En el plano cartesiano se puede suponer que el rango de la función arcotangente toma los valores (−π/2, π/2) (en radianes ), y se debe tener cierto cuidado para definir la función arcotangente más completa para los puntos ( x , y ) cuando x ≤ 0 . [nota 1] En el plano complejo estas coordenadas polares toman la forma
donde [nota 2]
Aquí | z | es el valor absoluto o módulo del número complejo z ; θ , el argumento de z , se toma usualmente en el intervalo 0 ≤ θ < 2 π ; y la última igualdad (a | z | e iθ ) se toma de la fórmula de Euler . Sin la restricción en el rango de θ , el argumento de z es multivaluado, porque la función exponencial compleja es periódica, con periodo 2 πi . Por lo tanto, si θ es un valor de arg( z ) , los otros valores están dados por arg( z ) = θ + 2 nπ , donde n es cualquier entero distinto de cero. [2]
Aunque rara vez se utiliza explícitamente, la visión geométrica de los números complejos se basa implícitamente en su estructura de un espacio vectorial euclidiano de dimensión 2, donde el producto interno de los números complejos w y z está dado por ; entonces, para un número complejo z, su valor absoluto | z | coincide con su norma euclidiana, y su argumento arg( z ) con el ángulo que gira de 1 a z .
La teoría de la integración de contornos comprende una parte importante del análisis complejo. En este contexto, la dirección de recorrido alrededor de una curva cerrada es importante: invertir la dirección en la que se recorre la curva multiplica el valor de la integral por −1 . Por convención, la dirección positiva es en sentido antihorario. Por ejemplo, el círculo unitario se recorre en dirección positiva cuando empezamos en el punto z = 1 , luego nos desplazamos hacia arriba y hacia la izquierda a través del punto z = i , luego hacia abajo y hacia la izquierda a través de −1 , luego hacia abajo y hacia la derecha a través de − i y, finalmente, hacia arriba y hacia la derecha hasta z = 1 , donde comenzamos.
Casi todo el análisis complejo se ocupa de funciones complejas , es decir, de funciones que asignan algún subconjunto del plano complejo a algún otro subconjunto (posiblemente superpuesto, o incluso idéntico) del plano complejo. Aquí se acostumbra hablar del dominio de f ( z ) como si estuviera en el plano z , mientras que se hace referencia al rango de f ( z ) como un conjunto de puntos en el plano w . En símbolos escribimos
y a menudo pensamos en la función f como una transformación del plano z (con coordenadas ( x , y ) ) al plano w (con coordenadas ( u , v ) ).
El plano complejo se denota como .
El diagrama de Argand se refiere a una representación geométrica de números complejos como puntos z = x + iy utilizando el eje horizontal x como eje real y el eje vertical y como eje imaginario. [3] Estos diagramas reciben su nombre de Jean-Robert Argand (1768-1822), aunque fueron descritos por primera vez por el agrimensor y matemático noruego-danés Caspar Wessel (1745-1818). [nota 3] Los diagramas de Argand se utilizan con frecuencia para representar gráficamente las posiciones de los ceros y polos de una función en el plano complejo.

Puede resultar útil pensar en el plano complejo como si ocupara la superficie de una esfera. Dada una esfera de radio unitario, coloque su centro en el origen del plano complejo, orientado de modo que el ecuador de la esfera coincida con el círculo unitario del plano y el polo norte esté "encima" del plano.
Podemos establecer una correspondencia biunívoca entre los puntos de la superficie de la esfera menos el polo norte y los puntos del plano complejo de la siguiente manera. Dado un punto en el plano, dibuja una línea recta que lo conecte con el polo norte de la esfera. Esa línea intersectará la superficie de la esfera en exactamente otro punto. El punto z = 0 se proyectará sobre el polo sur de la esfera. Como el interior del círculo unitario se encuentra dentro de la esfera, toda esa región ( | z | < 1 ) se proyectará sobre el hemisferio sur. El círculo unitario en sí ( | z | = 1 ) se proyectará sobre el ecuador, y el exterior del círculo unitario ( | z | > 1 ) se proyectará sobre el hemisferio norte, menos el polo norte. Claramente, este procedimiento es reversible: dado cualquier punto en la superficie de la esfera que no sea el polo norte, podemos dibujar una línea recta que conecte ese punto con el polo norte e interseque el plano en exactamente un punto.
En esta proyección estereográfica, el polo norte en sí no está asociado con ningún punto en el plano complejo. Perfeccionamos la correspondencia biunívoca añadiendo un punto más al plano complejo –el llamado punto en el infinito– e identificándolo con el polo norte en la esfera. Este espacio topológico, el plano complejo más el punto en el infinito, se conoce como el plano complejo extendido . Hablamos de un único "punto en el infinito" cuando hablamos de análisis complejo. Hay dos puntos en el infinito (positivo y negativo) en la línea de números reales , pero sólo hay un punto en el infinito (el polo norte) en el plano complejo extendido. [5]
Imaginemos por un momento qué sucederá con las líneas de latitud y longitud cuando se proyecten desde la esfera sobre la superficie plana. Las líneas de latitud son todas paralelas al ecuador, por lo que se convertirán en círculos perfectos centrados en el origen z = 0. Y las líneas de longitud se convertirán en líneas rectas que pasan por el origen (y también por el "punto en el infinito", ya que pasan por los polos norte y sur de la esfera).
Esta no es la única situación estereográfica posible y plausible de la proyección de una esfera sobre un plano formado por dos o más valores. Por ejemplo, el polo norte de la esfera podría estar situado encima del origen z = −1 en un plano que es tangente al círculo. Los detalles no importan realmente. Cualquier proyección estereográfica de una esfera sobre un plano producirá un "punto en el infinito", y convertirá las líneas de latitud y longitud de la esfera en círculos y líneas rectas, respectivamente, en el plano.
Cuando se habla de funciones de variable compleja, suele ser conveniente pensar en un corte en el plano complejo. Esta idea surge de forma natural en varios contextos diferentes.
Considere la simple relación de dos valores
Antes de que podamos tratar esta relación como una función univaluada , el rango del valor resultante debe restringirse de alguna manera. Cuando se trabaja con raíces cuadradas de números reales no negativos, esto se hace fácilmente. Por ejemplo, podemos simplemente definir
es el número real no negativo y tal que y 2 = x . Esta idea no funciona tan bien en el plano complejo bidimensional. Para ver por qué, pensemos en la forma en que el valor de f ( z ) varía a medida que el punto z se mueve alrededor del círculo unitario. Podemos escribir y tomar
Evidentemente, a medida que z se desplaza por todo el círculo, w solo recorre la mitad del círculo. Por lo tanto, un movimiento continuo en el plano complejo ha transformado la raíz cuadrada positiva e 0 = 1 en la raíz cuadrada negativa e iπ = −1 .
Este problema surge porque el punto z = 0 tiene sólo una raíz cuadrada, mientras que cualquier otro número complejo z ≠ 0 tiene exactamente dos raíces cuadradas. En la línea de números reales podríamos evitar este problema erigiendo una "barrera" en el único punto x = 0 . Se necesita una barrera más grande en el plano complejo, para evitar que cualquier contorno cerrado rodee completamente el punto de ramificación z = 0 . Esto se hace comúnmente introduciendo un corte de ramificación ; en este caso el "corte" podría extenderse desde el punto z = 0 a lo largo del eje real positivo hasta el punto en el infinito, de modo que el argumento de la variable z en el plano de corte esté restringido al rango 0 ≤ arg( z ) < 2 π .
Ahora podemos dar una descripción completa de w = z 1/2 . Para ello necesitamos dos copias del plano z , cada una de ellas cortada a lo largo del eje real. En una copia definimos la raíz cuadrada de 1 como e 0 = 1 , y en la otra definimos la raíz cuadrada de 1 como e iπ = −1 . Llamamos a estas dos copias del plano de corte completo sheets . Al hacer un argumento de continuidad vemos que la función (ahora univaluada) w = z 1/2 mapea la primera sheet en la mitad superior del plano w , donde 0 ≤ arg( w ) < π , mientras que mapea la segunda sheet en la mitad inferior del plano w (donde π ≤ arg( w ) < 2 π ). [6]
En este ejemplo, el corte de la rama no tiene por qué estar a lo largo del eje real; ni siquiera tiene que ser una línea recta. Cualquier curva continua que conecte el origen z = 0 con el punto en el infinito funcionaría. En algunos casos, el corte de la rama ni siquiera tiene que pasar por el punto en el infinito. Por ejemplo, considere la relación
Aquí el polinomio z 2 − 1 se anula cuando z = ±1 , por lo que g evidentemente tiene dos puntos de ramificación. Podemos "cortar" el plano a lo largo del eje real, desde −1 hasta 1 , y obtener una hoja en la que g ( z ) es una función univaluada. Alternativamente, el corte puede ir desde z = 1 a lo largo del eje real positivo a través del punto en el infinito, y luego continuar "hacia arriba" por el eje real negativo hasta el otro punto de ramificación, z = −1 .
Esta situación se visualiza más fácilmente utilizando la proyección estereográfica descrita anteriormente. En la esfera, uno de estos cortes corre longitudinalmente a través del hemisferio sur, conectando un punto en el ecuador ( z = −1 ) con otro punto en el ecuador ( z = 1 ), y pasando por el polo sur (el origen, z = 0 ) en el camino. La segunda versión del corte corre longitudinalmente a través del hemisferio norte y conecta los mismos dos puntos ecuatoriales pasando por el polo norte (es decir, el punto en el infinito).
Una función meromórfica es una función compleja que es holomorfa y, por lo tanto, analítica en todas partes de su dominio, excepto en un número finito o infinito numerable de puntos. [nota 4] Los puntos en los que no se puede definir una función de este tipo se denominan polos de la función meromórfica. A veces, todos estos polos se encuentran en una línea recta. En ese caso, los matemáticos pueden decir que la función es "holomórfica en el plano de corte". Por ejemplo:
La función gamma , definida por
donde γ es la constante de Euler-Mascheroni , y tiene polos simples en 0, −1, −2, −3, ... porque exactamente un denominador en el producto infinito se desvanece cuando z = 0 , o un entero negativo. [nota 5] Dado que todos sus polos se encuentran en el eje real negativo, desde z = 0 hasta el punto en el infinito, esta función podría describirse como "holomórfica en el plano de corte, el corte se extiende a lo largo del eje real negativo, desde 0 (incluido) hasta el punto en el infinito".
Alternativamente, Γ( z ) podría describirse como "holomorfo en el plano de corte con − π < arg( z ) < π y excluyendo el punto z = 0 ".
Este corte es ligeramente diferente del corte de ramificación que ya hemos encontrado, porque en realidad excluye el eje real negativo del plano de corte. El corte de ramificación dejó el eje real conectado con el plano de corte en un lado (0 ≤ θ ) , pero lo separó del plano de corte a lo largo del otro lado ( θ < 2 π ) .
Por supuesto, no es realmente necesario excluir todo el segmento de línea de z = 0 a −∞ para construir un dominio en el que Γ( z ) sea holomorfo. Todo lo que realmente tenemos que hacer es perforar el plano en un conjunto infinito numerable de puntos {0, −1, −2, −3, ...} . Pero un contorno cerrado en el plano perforado podría rodear uno o más de los polos de Γ( z ) , dando una integral de contorno que no es necesariamente cero, por el teorema del residuo . Cortar el plano complejo asegura no solo que Γ( z ) sea holomorfo en este dominio restringido, sino también que la integral de contorno de la función gamma sobre cualquier curva cerrada que se encuentre en el plano de corte sea idénticamente igual a cero.
Muchas funciones complejas se definen mediante series infinitas o fracciones continuas . Una consideración fundamental en el análisis de estas expresiones infinitamente largas es identificar la porción del plano complejo en la que convergen a un valor finito. Un corte en el plano puede facilitar este proceso, como lo muestran los siguientes ejemplos.
Consideremos la función definida por la serie infinita
Como z 2 = (− z ) 2 para cada número complejo z , es claro que f ( z ) es una función par de z , por lo que el análisis puede restringirse a la mitad del plano complejo. Y como la serie no está definida cuando
Tiene sentido cortar el plano a lo largo de todo el eje imaginario y establecer la convergencia de esta serie donde la parte real de z no es cero antes de emprender la tarea más ardua de examinar f ( z ) cuando z es un número imaginario puro. [nota 6]
En este ejemplo, el corte es una mera conveniencia, porque los puntos en los que la suma infinita no está definida están aislados, y el plano de corte puede reemplazarse por un plano perforado de manera adecuada . En algunos contextos, el corte es necesario, y no solo conveniente. Consideremos la fracción continua periódica infinita
Se puede demostrar que f ( z ) converge a un valor finito si z no es un número real negativo tal que z < − 1 ⁄ 4 . En otras palabras, la región de convergencia para esta fracción continua es el plano de corte, donde el corte corre a lo largo del eje real negativo, desde − 1 ⁄ 4 hasta el punto en el infinito. [8]
Ya hemos visto cómo es la relación
se puede convertir en una función univaluada dividiendo el dominio de f en dos láminas desconectadas. También es posible "pegar" esas dos láminas para formar una única superficie de Riemann en la que f ( z ) = z 1/2 se puede definir como una función holomorfa cuya imagen es todo el plano w (excepto el punto w = 0 ). Así es como funciona.
Imaginemos dos copias del plano complejo de corte, en las que los cortes se extienden a lo largo del eje real positivo desde z = 0 hasta el punto en el infinito. En una hoja, definamos 0 ≤ arg( z ) < 2 π , de modo que 1 1/2 = e 0 = 1 , por definición. En la segunda hoja, definamos 2 π ≤ arg( z ) < 4 π , de modo que 1 1/2 = e iπ = −1 , nuevamente por definición. Ahora voltea la segunda hoja boca abajo, de modo que el eje imaginario apunte en la dirección opuesta del eje imaginario en la primera hoja, con ambos ejes reales apuntando en la misma dirección, y "pega" las dos hojas juntas (de modo que el borde en la primera hoja etiquetado " θ = 0 " esté conectado al borde etiquetado " θ < 4 π " en la segunda hoja, y el borde en la segunda hoja etiquetado " θ = 2 π " esté conectado al borde etiquetado " θ < 2 π " en la primera hoja). El resultado es el dominio de superficie de Riemann en el que f ( z ) = z 1/2 es univaluado y holomorfo (excepto cuando z = 0 ). [6]
Para entender por qué f es univaluada en este dominio, imaginemos un circuito alrededor del círculo unitario, comenzando con z = 1 en la primera hoja. Cuando 0 ≤ θ < 2 π todavía estamos en la primera hoja. Cuando θ = 2 π hemos pasado a la segunda hoja, y estamos obligados a hacer un segundo circuito completo alrededor del punto de ramificación z = 0 antes de regresar a nuestro punto de partida, donde θ = 4 π es equivalente a θ = 0 , debido a la forma en que pegamos las dos hojas. En otras palabras, como la variable z da dos vueltas completas alrededor del punto de ramificación, la imagen de z en el plano w traza solo un círculo completo.
La diferenciación formal muestra que
de lo cual podemos concluir que la derivada de f existe y es finita en todas partes de la superficie de Riemann, excepto cuando z = 0 (es decir, f es holomorfa, excepto cuando z = 0 ).
¿Cómo se puede encontrar la superficie de Riemann para la función?
También se discutió anteriormente, ¿se puede construir? Una vez más comenzamos con dos copias del plano z , pero esta vez cada una se corta a lo largo del segmento de línea real que se extiende desde z = −1 a z = 1 – estos son los dos puntos de ramificación de g ( z ) . Damos vuelta una de estas al revés, de modo que los dos ejes imaginarios apunten en direcciones opuestas, y pegamos los bordes correspondientes de las dos hojas cortadas. Podemos verificar que g es una función de un solo valor en esta superficie trazando un circuito alrededor de un círculo de radio unitario centrado en z = 1 . Comenzando en el punto z = 2 en la primera hoja, giramos la mitad del círculo antes de encontrar el corte en z = 0 . El corte nos obliga a pasar a la segunda hoja, de modo que cuando z ha dado una vuelta completa alrededor del punto de ramificación z = 1 , w ha dado sólo la mitad de una vuelta completa, el signo de w se ha invertido (porque e iπ = −1 ), y nuestro camino nos ha llevado al punto z = 2 en la segunda hoja de la superficie. Continuando con otra media vuelta encontramos el otro lado del corte, donde z = 0 , y finalmente llegamos a nuestro punto de partida ( z = 2 en la primera hoja) después de dar dos vueltas completas alrededor del punto de ramificación.
La forma natural de etiquetar θ = arg( z ) en este ejemplo es establecer − π < θ ≤ π en la primera hoja, con π < θ ≤ 3 π en la segunda. Los ejes imaginarios en las dos hojas apuntan en direcciones opuestas de modo que el sentido antihorario de rotación positiva se conserva a medida que un contorno cerrado se mueve de una hoja a la otra (recuerde, la segunda hoja está al revés ). Imagine esta superficie incrustada en un espacio tridimensional, con ambas hojas paralelas al plano xy . Entonces parece haber un agujero vertical en la superficie, donde se unen los dos cortes. ¿Qué pasa si el corte se hace desde z = −1 hacia abajo del eje real hasta el punto en el infinito, y desde z = 1 , hacia arriba del eje real hasta que el corte se encuentra consigo mismo? Nuevamente se puede construir una superficie de Riemann, pero esta vez el "agujero" es horizontal. Topológicamente hablando , ambas versiones de esta superficie de Riemann son equivalentes: son superficies bidimensionales orientables de género uno.
En la teoría de control , un uso del plano complejo se conoce como plano s . Se utiliza para visualizar gráficamente las raíces de la ecuación que describe el comportamiento de un sistema (la ecuación característica). La ecuación normalmente se expresa como un polinomio en el parámetro s de la transformada de Laplace , de ahí el nombre de plano s . Los puntos en el plano s toman la forma s = σ + jω , donde se utiliza " j " en lugar de la habitual " i " para representar el componente imaginario (la variable " i " se utiliza a menudo para denotar la corriente eléctrica en contextos de ingeniería).
Otro uso relacionado del plano complejo es el criterio de estabilidad de Nyquist . Se trata de un principio geométrico que permite determinar la estabilidad de un sistema de retroalimentación de bucle cerrado mediante la inspección de un diagrama de Nyquist de su magnitud y respuesta de fase de bucle abierto en función de la frecuencia (o función de transferencia de bucle ) en el plano complejo.
El plano z es una versión de tiempo discreto del plano s , donde se utilizan transformadas z en lugar de la transformación de Laplace.
El plano complejo está asociado con dos espacios cuadráticos distintos . Para un punto z = x + iy en el plano complejo, la función de cuadratura z 2 y la norma al cuadrado x 2 + y 2 son ambas formas cuadráticas . La primera se descuida con frecuencia a raíz del uso de la segunda para establecer una métrica en el plano complejo. Estas caras distintas del plano complejo como espacio cuadrático surgen en la construcción de álgebras sobre un cuerpo con el proceso de Cayley-Dickson . Ese procedimiento se puede aplicar a cualquier cuerpo , y se producen diferentes resultados para los cuerpos R y C : cuando R es el cuerpo de despegue, entonces C se construye con la forma cuadrática x 2 + y 2 , pero el proceso también puede comenzar con C y z 2 , y ese caso genera álgebras que difieren de las derivadas de R. En cualquier caso, las álgebras generadas son álgebras de composición ; en este caso, el plano complejo es el conjunto de puntos para dos álgebras de composición distintas.
Las secciones anteriores de este artículo tratan del plano complejo en términos de una representación geométrica de los números complejos. Aunque este uso del término "plano complejo" tiene una larga y rica historia matemática, no es de ninguna manera el único concepto matemático que puede caracterizarse como "plano complejo". Existen al menos tres posibilidades adicionales.