El Commentariolus ( Pequeño comentario ) es un breve bosquejo de Nicolás Copérnico de una versión temprana de su revolucionaria teoría heliocéntrica del universo. [1] Después de un largo desarrollo de su teoría, Copérnico publicó la versión madura en 1543 en su obra histórica, De revolutionibus orbium coelestium ( Sobre las revoluciones de las esferas celestes ).
Copérnico escribió el Commentariolus en latín en 1514 y distribuyó copias entre sus amigos y colegas. [a] De este modo se hizo conocido entre los contemporáneos de Copérnico, aunque nunca se imprimió durante su vida. En 1533, Johann Albrecht Widmannstetter pronunció una serie de conferencias en Roma en las que describió la teoría de Copérnico. El papa Clemente VII y varios cardenales católicos escucharon las conferencias y se interesaron por la teoría. El 1 de noviembre de 1536, Nikolaus von Schönberg , arzobispo de Capua y desde el año anterior cardenal, escribió a Copérnico desde Roma y le pidió una copia de sus escritos "lo antes posible". [4]
Aunque copias del Commentariolus circularon durante un tiempo después de la muerte de Copérnico, [b] posteriormente cayó en el olvido y su existencia previa permaneció conocida sólo indirectamente, hasta que se descubrió y publicó una copia manuscrita sobreviviente en la segunda mitad del siglo XIX. [c]
El Commentariolus se subdivide en ocho secciones (o capítulos), de las cuales todas, salvo la primera, llevan breves títulos descriptivos. Tras una breve introducción, la primera sección enuncia siete postulados a partir de los cuales Copérnico se propone demostrar que el movimiento aparente de los planetas puede explicarse sistemáticamente. [7]
Las siete secciones restantes se titulan, en orden, De ordine orbium ( "El orden de las esferas" ), De motibus qui circa solem aparente ( "Los movimientos aparentes del Sol" ), Quod aequalitas motum non ad aequinoctia sed ad stellas fixas referatur ( "El movimiento igual no debe medirse por los equinoccios sino por las estrellas fijas" ), De Luna ( "La Luna " ), De tribus superioribus: Saturno, Jove et Marte ( "Los planetas exteriores: Saturno , Júpiter y Marte " ), De Venere ( " Venus " ) y De Mercurio ( " Mercurio " ). [8]
En esta sección se presentan las esferas celestes en orden de la más exterior a la más interior. La esfera más exterior es la de las estrellas fijas, que permanece perfectamente estacionaria. A continuación siguen las de Saturno, Júpiter, Marte, la Tierra, Venus y Mercurio, que giran cada una alrededor del Sol de oeste a este con períodos de revolución sucesivamente más cortos: Saturno dura entre 29 y 30 años, Júpiter entre 11 y 12, Marte entre 2 y 3, la Tierra exactamente uno, Venus entre 8 y 9 meses, [d] y Mercurio entre 2 y 3 meses. La esfera de la Luna, en cambio, gira alrededor de la Tierra en un período de un mes, y se mueve con ella alrededor del Sol como un epiciclo .
En esta sección se explica cómo el movimiento aparente del Sol puede surgir de tres movimientos separados de la Tierra. El primer movimiento es una revolución uniforme, con un período de un año, de oeste a este a lo largo de una órbita circular cuyo centro está desplazado del Sol en 1/25 del radio de la órbita.
El segundo movimiento es la rotación diaria alrededor de un eje que pasa por el centro de la Tierra y está inclinado un ángulo de aproximadamente 23 1 ⁄ 2 ° con respecto a la perpendicular al plano de su órbita.
El tercer movimiento es la precesión del eje de rotación de la Tierra alrededor de un eje perpendicular al plano de su órbita. Copérnico especificó que la velocidad de esta precesión con respecto a la línea radial que va desde la Tierra hasta el centro de su órbita era algo inferior a un año, con una dirección implícita de oeste a este. Con respecto a las estrellas fijas , esta precesión es muy lenta y en dirección opuesta (de este a oeste) y explica el fenómeno de la precesión de los equinoccios .
Copérnico afirma aquí que el movimiento de los equinoccios y de los polos celestes no ha sido uniforme y sostiene que, en consecuencia, no deberían utilizarse para definir el marco de referencia con respecto al cual se miden los movimientos de los planetas, y que los períodos de los diversos movimientos planetarios se pueden determinar con mayor precisión si esos movimientos se miden con respecto a las estrellas fijas. Sostiene que había descubierto que la duración del año sideral siempre había sido de 365 días, 6 horas y 10 minutos. [e]
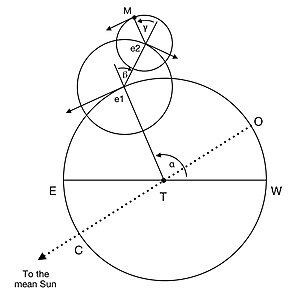
Copérnico explica el movimiento de la Luna como compuesto de cinco movimientos independientes, incluyendo la revolución anual alrededor del Sol, que la Luna comparte con la Tierra en su sistema. Su movimiento alrededor de la Tierra se encuentra en un plano inclinado en un ángulo de 5° respecto al plano de la órbita terrestre, y que precesa de este a oeste alrededor de un eje perpendicular a ese plano, con un período de entre 18 y 19 años con respecto a las estrellas fijas. Los tres movimientos restantes, que tienen lugar dentro de este plano orbital, se representan en el diagrama de la derecha. El primero de ellos es el del primero, y más grande, de dos epiciclos , cuyo centro (representado por el punto e1 en el diagrama) se mueve uniformemente de oeste a este alrededor de la circunferencia de un deferente centrado en la Tierra (representado por el punto T en el diagrama), con un período de un mes draconítico . [f] El centro del segundo epiciclo, más pequeño (representado por el punto e2 en el diagrama) se mueve uniformemente de este a oeste alrededor de la circunferencia del primero, de modo que el período del ángulo β en el diagrama es un mes anómalo . [9]
La Luna, representada por el punto M en el diagrama, se mueve uniformemente de oeste a este alrededor de la circunferencia del segundo epiciclo, de modo que el período del ángulo γ es la mitad de un mes sinódico . [9] Copérnico afirma que siempre que el punto e1 se encuentre en la línea que une la Tierra con el centro de su órbita (representada por la línea de puntos OTC en el diagrama, de la que solo el punto T se encuentra aquí en el plano orbital de la Luna), la Luna M se encontrará precisamente entre e1 y e2. Sin embargo, esto solo puede ocurrir una vez cada 19 años, cuando esta línea coincide con la línea de nodos WTE. En otras ocasiones, no se encuentra en el plano orbital de la Luna y, por lo tanto, el punto e1 no puede pasar por él. En general, entonces, aunque la Luna estará cerca de la conjunción u oposición al Sol siempre que se encuentre precisamente entre e1 y e2, estos eventos no serán precisamente simultáneos.
La relación que Copérnico tomó como referencia para las longitudes relativas del epiciclo pequeño, el epiciclo grande y el deferente es 4:19:180.
Las teorías que Copérnico propone en el Commentariolus sobre los movimientos de los planetas exteriores tienen todas la misma estructura general y sólo difieren en los valores de los diversos parámetros necesarios para especificar completamente sus movimientos. Sus órbitas no son coplanares con la de la Tierra, pero sí comparten su centro como centro común propio y se encuentran en planos que están sólo ligeramente inclinados respecto del plano orbital de la Tierra. A diferencia del plano orbital de la Luna, las de los planetas superiores no precesan. Sin embargo, sus inclinaciones respecto del plano orbital de la Tierra oscilan entre los límites de 0°10′ y 1°50′ para Marte, 1°15′ y 1°40′ para Júpiter, y 2°15′ y 2°40′ para Saturno. Aunque Copérnico supone que estas oscilaciones tienen lugar alrededor de las líneas de nodos de las órbitas , que supone que permanecen fijas, el mecanismo que utiliza para modelarlas también provoca pequeñas oscilaciones en las líneas de nodos. Como Kepler señaló más tarde, la necesidad de suponer oscilaciones en las inclinaciones de los planos orbitales de los planetas exteriores es un efecto de Copérnico, al suponer que pasan por el centro de la órbita de la Tierra. Si hubiera supuesto que pasan por el Sol, no habría necesitado introducir estas oscilaciones. [10]

Al igual que el movimiento de la Luna, el de los planetas exteriores, representado en el diagrama de la derecha, se produce por una combinación de un deferente y dos epiciclos. El centro del primero y más grande de los dos epiciclos, representado por el punto e1 en el diagrama, gira uniformemente de oeste a este alrededor de la circunferencia de un deferente cuyo centro es el centro de la órbita de la Tierra, representada por el punto S en el diagrama, con un período relativo a las estrellas fijas como el que se indica en la sección El orden de las esferas anterior.
El centro del segundo epiciclo, representado por el punto e2 en el diagrama, gira uniformemente de este a oeste alrededor de la circunferencia del primero, con el mismo período relativo a la línea radial que une S con e1. Como consecuencia, la dirección de la línea radial que une e1 con e2 permanece fija con respecto a las estrellas fijas, paralela a la línea de ábsides del planeta EW, y el punto e2 describe un círculo excéntrico [g] cuyo radio es igual al del deferente, y cuyo centro, representado por el punto O en el diagrama, está desplazado del deferente por el radio del primer epiciclo. En su obra posterior, De revolutionibus orbium coelestium , Copérnico utiliza este círculo excéntrico directamente, en lugar de representarlo como una combinación de un deferente y un epiciclo.
El planeta, representado por el punto P en el diagrama, gira uniformemente de oeste a este alrededor de la circunferencia del segundo epiciclo, cuyo radio es exactamente un tercio del primero, a una velocidad de revolución dos veces mayor que la de e1 alrededor de S. Este mecanismo permitió a Copérnico prescindir del ecuante , una característica muy criticada de las teorías de Claudio Ptolomeo para los movimientos de los planetas exteriores. En una versión heliocéntrica de los modelos de Ptolomeo, su ecuante estaría en el punto Q del diagrama, desplazado a lo largo de la línea de ábsides EW desde el punto S por una distancia una vez y un tercio el radio del primer epiciclo de Copérnico. El centro del deferente del planeta, con el mismo radio que el de Copérnico, estaría en el punto C, a medio camino entre S y Q. El planeta mismo estaría en el punto de intersección de este deferente con la línea QP. Si bien este punto sólo coincide exactamente con P cuando ambos están en un ábside , [h] la diferencia entre sus posiciones es siempre insignificante en comparación con las inexactitudes inherentes a ambas teorías.
En cuanto a las razones entre los radios de los deferentes de los planetas exteriores y el radio de la Tierra, el Commentariolus da 1 13 ⁄ 25 para Marte, 5 13 ⁄ 60 para Júpiter y 9 7 ⁄ 30 para Saturno. En cuanto a las razones entre los radios de sus deferentes y los radios de sus epiciclos más grandes, da 6 138 ⁄ 167 para Marte, 12 553 ⁄ 606 para Júpiter y 11 859 ⁄ 1181 para Saturno. [i]
En las dos últimas secciones Copérnico habla de Venus y Mercurio. El primero tiene un sistema de círculos y tarda nueve meses en completar una revolución.
La órbita de Mercurio es más difícil de estudiar que la de cualquier otro planeta, ya que sólo es visible unos pocos días al año. Mercurio, al igual que Venus, tiene dos epiciclos, uno mayor que el otro. Tarda casi tres meses en completar una revolución.