
En dinámica de fluidos , el proceso por el cual un flujo laminar se vuelve turbulento se conoce como transición laminar-turbulenta . El parámetro principal que caracteriza la transición es el número de Reynolds .
La transición suele describirse como un proceso que se desarrolla a través de una serie de etapas. El flujo de transición puede referirse a una transición en cualquier dirección, es decir, flujo de transición laminar-turbulento o flujo de transición turbulento-laminar.
El proceso se aplica a cualquier flujo de fluido y se utiliza con mayor frecuencia en el contexto de capas límite .
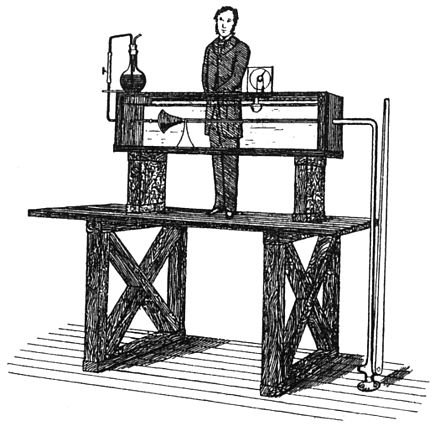

En 1883, Osborne Reynolds demostró la transición al flujo turbulento en un experimento clásico en el que examinó el comportamiento del flujo de agua bajo diferentes velocidades de flujo utilizando un pequeño chorro de agua teñida introducido en el centro del flujo en una tubería más grande.
El tubo más grande era de vidrio, por lo que se podía observar el comportamiento de la capa de flujo teñido, y al final de este tubo había una válvula de control de flujo que se utilizaba para variar la velocidad del agua dentro del tubo. Cuando la velocidad era baja, la capa teñida se mantenía nítida a lo largo de toda la longitud del tubo grande. Cuando la velocidad aumentaba, la capa se rompía en un punto determinado y se difundía por toda la sección transversal del fluido. El punto en el que esto sucedía era el punto de transición del flujo laminar al turbulento. Reynolds identificó el parámetro que regulaba el inicio de este efecto, que era una constante adimensional que más tarde se denominó número de Reynolds .
Reynolds descubrió que la transición se producía entre Re = 2000 y 13000, dependiendo de la suavidad de las condiciones de entrada. Si se tiene mucho cuidado, la transición puede producirse incluso con un Re tan alto como 40000. Por otro lado, Re = 2000 parece ser el valor más bajo obtenido en una entrada irregular. [1]
Las publicaciones de Reynolds sobre dinámica de fluidos comenzaron a principios de la década de 1870. Su modelo teórico final, publicado a mediados de la década de 1890, sigue siendo el marco matemático estándar que se utiliza en la actualidad. Algunos ejemplos de títulos de sus informes más innovadores son:

Una capa límite puede pasar a la turbulencia a través de varios caminos. El camino que se realiza físicamente depende de las condiciones iniciales, como la amplitud inicial de la perturbación y la rugosidad de la superficie. El nivel de comprensión de cada fase varía enormemente, desde una comprensión casi completa del crecimiento del modo primario hasta una falta casi total de comprensión de los mecanismos de derivación .
La etapa inicial del proceso de transición natural se conoce como fase de receptividad y consiste en la transformación de perturbaciones ambientales, tanto acústicas (sonido) como vorticiales (turbulencia), en pequeñas perturbaciones dentro de la capa límite. Los mecanismos por los cuales surgen estas perturbaciones son variados e incluyen el sonido de corriente libre y/o la turbulencia interactuando con la curvatura de la superficie, discontinuidades de forma y rugosidad de la superficie. Estas condiciones iniciales son pequeñas perturbaciones, a menudo inmensurables, del flujo en estado básico. A partir de aquí, el crecimiento (o decaimiento) de estas perturbaciones depende de la naturaleza de la perturbación y de la naturaleza del estado básico. Las perturbaciones acústicas tienden a excitar inestabilidades bidimensionales como las ondas de Tollmien-Schlichting (ondas TS), mientras que las perturbaciones vorticiales tienden a conducir al crecimiento de fenómenos tridimensionales como la inestabilidad de flujo cruzado. [3]
Numerosos experimentos realizados en las últimas décadas han revelado que la extensión de la región de amplificación y, por lo tanto, la ubicación del punto de transición en la superficie corporal, depende en gran medida no solo de la amplitud y/o el espectro de las perturbaciones externas, sino también de su naturaleza física. Algunas de las perturbaciones penetran fácilmente en la capa límite, mientras que otras no. En consecuencia, el concepto de transición de la capa límite es complejo y aún carece de una exposición teórica completa.
Si la perturbación inicial generada por el medio ambiente es lo suficientemente pequeña, la siguiente etapa del proceso de transición es la del crecimiento del modo primario. En esta etapa, las perturbaciones iniciales crecen (o decaen) de la manera descrita por la teoría de la estabilidad lineal . [4] Las inestabilidades específicas que se exhiben en la realidad dependen de la geometría del problema y de la naturaleza y amplitud de las perturbaciones iniciales. En un rango de números de Reynolds en una configuración de flujo dada, los modos más amplificados pueden variar y, a menudo, lo hacen.
Existen varios tipos principales de inestabilidad que ocurren comúnmente en las capas límite. En los flujos subsónicos y en los primeros flujos supersónicos, las inestabilidades bidimensionales dominantes son las ondas TS. Para los flujos en los que se desarrolla una capa límite tridimensional, como un ala en flecha, la inestabilidad de flujo cruzado se vuelve importante. Para los flujos que navegan por una curvatura de superficie cóncava, los vórtices de Görtler pueden convertirse en la inestabilidad dominante. Cada inestabilidad tiene sus propios orígenes físicos y su propio conjunto de estrategias de control, algunas de las cuales están contraindicadas por otras inestabilidades, lo que aumenta la dificultad de controlar la transición laminar-turbulenta.
El sonido armónico simple como factor desencadenante de la transición repentina de flujo laminar a turbulento podría atribuirse a Elizabeth Barrett Browning . Su poema Aurora Leigh (1856) reveló cómo las notas musicales (el repique de una campana de iglesia en particular) desencadenaban una turbulencia vacilante en las llamas de flujo laminar previamente constante de las farolas de gas de la calle (“... las farolas de gas tiemblan en las calles y plazas” [5] ). Su poema, aclamado al instante, podría haber alertado a los científicos (por ejemplo, Leconte 1859) sobre la influencia del sonido armónico simple (SH) como causa de turbulencia. Una oleada contemporánea de interés científico en este efecto culminó con Sir John Tyndall (1867) deduciendo que los sonidos SH específicos, dirigidos perpendicularmente al flujo, tenían ondas que se mezclaban con ondas SH similares creadas por la fricción a lo largo de los límites de los tubos, amplificándolas y desencadenando el fenómeno del flujo turbulento de alta resistencia. Su interpretación resurgió más de 100 años después (Hamilton 2015).
Walter Tollmien (1931) y Hermann Schlichting (1929) propusieron que la fricción (viscosidad) a lo largo de un límite plano liso, creaba oscilaciones de la capa límite (BL) de SH que aumentaban gradualmente en amplitud hasta que estallaba la turbulencia. [6] [7] Aunque los túneles de viento contemporáneos no pudieron confirmar la teoría, Schubauer y Skramstad (1943) crearon un túnel de viento refinado que amortiguaba las vibraciones y los sonidos que podrían incidir en los estudios de flujo de placa plana del túnel de viento. Confirmaron el desarrollo de oscilaciones de BL de cresta larga de SH, las ondas de corte dinámicas de transición a la turbulencia. Demostraron que vibraciones de aleteo específicas de SH inducidas electromagnéticamente en una cinta ferromagnética de BL podían amplificar ondas de aleteo de BL (BLF) de SH inducidas por flujo similares, precipitando turbulencia a velocidades de flujo mucho más bajas. Además, ciertas otras frecuencias específicas interferían con el desarrollo de las ondas BLF de SH, preservando el flujo laminar a velocidades de flujo más altas.
Una oscilación de una masa en un fluido es una vibración que crea una onda sonora. Las oscilaciones SH BLF en el fluido de la capa límite a lo largo de una placa plana deben producir sonido SH que se refleje en el límite perpendicular a las láminas del fluido. En la transición tardía, Schubauer y Skramstad encontraron focos de amplificación de las oscilaciones BL, asociados con ráfagas de ruido ("puntos turbulentos"). La amplificación focal del sonido transversal en la transición tardía se asoció con la formación de vórtices BL.
El sonido amplificado focal de puntos turbulentos a lo largo de una placa plana con oscilación de alta energía de moléculas perpendicularmente a través de las láminas, podría causar de repente un congelamiento localizado del deslizamiento laminar. El frenado repentino de puntos “congelados” de fluido transferiría resistencia a la alta resistencia en el límite, y podría explicar los vórtices de BL que se desbordan de lado a lado en la transición tardía. Osborne Reynolds describió puntos turbulentos similares durante la transición en el flujo de agua en cilindros (“destellos de turbulencia”). [8]
Cuando estallan muchos vórtices aleatorios como inicios de la turbulencia, la congelación generalizada del deslizamiento laminar (enclavamiento laminar) se asocia con ruido y un aumento dramático en la resistencia al flujo. Esto también podría explicar el cambio abrupto del perfil de isovelocidad parabólica del flujo laminar al perfil aplanado del flujo turbulento, ya que el deslizamiento laminar es reemplazado por el enclavamiento laminar a medida que estalla la turbulencia (Hamilton 2015). [9]
Los modos primarios en sí mismos no conducen directamente a la ruptura, sino que conducen a la formación de mecanismos de inestabilidad secundaria. A medida que los modos primarios crecen y distorsionan el flujo medio, comienzan a exhibir no linealidades y la teoría lineal ya no se aplica. Para complicar el asunto, está la creciente distorsión del flujo medio, que puede conducir a puntos de inflexión en el perfil de velocidad, una situación que Lord Rayleigh demostró que indica una inestabilidad absoluta en una capa límite. Estas inestabilidades secundarias conducen rápidamente a la ruptura. Estas inestabilidades secundarias suelen tener una frecuencia mucho más alta que sus precursoras lineales.