En matemáticas combinatorias , un toro de De Bruijn , llamado así por el matemático holandés Nicolaas Govert de Bruijn , es una matriz de símbolos de un alfabeto (a menudo solo 0 y 1) que contiene cada matriz posible de dimensiones dadas m × n exactamente una vez. Es un toro porque las aristas se consideran envolventes con el propósito de encontrar matrices. Su nombre proviene de la secuencia de De Bruijn , que puede considerarse un caso especial donde n = 1 (una dimensión).
Una de las principales preguntas abiertas con respecto a los toros de De Bruijn es si se puede construir un toro de De Bruijn para un tamaño de alfabeto particular para un m y n dados . Se sabe que estos siempre existen cuando n = 1 , ya que entonces simplemente obtenemos las secuencias de De Bruijn, que siempre existen. También se sabe que existen toros "cuadrados" siempre que m = n y pares (para el caso impar, los toros resultantes no pueden ser cuadrados). [1] [2] [3]
El toro de Bruijn "cuadrado" binario más pequeño posible, representado arriba a la derecha, denotado como toro de Bruijn (4,4;2,2) 2 (o simplemente como B 2 ), contiene todas las matrices binarias 2×2 .
Aparte de la "traducción", la "inversión" (intercambio de 0 y 1) y la "rotación" (de 90 grados), no son posibles otros 2 toros de Bruijn (4,4;2,2) – esto se puede demostrar mediante una inspección completa de las 2 16 matrices binarias (o subconjunto que cumpla restricciones tales como números iguales de 0 y 1). [4]
El toro puede desenrollarse repitiendo n −1 filas y columnas. Todas las submatrices n × n sin envoltura, como la sombreada en amarillo, forman entonces el conjunto completo:
_2_de_Bruijn_torus.svg/1280px-Visualisation_of_a_(256,256;4,4)_2_de_Bruijn_torus.svg.png)
Se ha construido explícitamente un ejemplo del siguiente posible toro de Bruijn "cuadrado" binario, (256,256;4,4) 2 (abreviado como B 4 ). [5]
La imagen de la derecha muestra un ejemplo de un toro/matriz de Bruijn (256,256;4,4) 2 , donde los ceros se han codificado como píxeles blancos y los unos como píxeles rojos respectivamente.
El artículo en el que se construyó un ejemplo del toro de Bruijn (256,256;4,4) 2 contenía más de 10 páginas de binario, a pesar de su tamaño de fuente reducido, que requería tres líneas por fila de la matriz.
El posible toro de Bruijn binario subsiguiente, que contiene todas las matrices binarias 6×6 , tendría 2 36 = 68.719.476.736 entradas, lo que daría como resultado una matriz cuadrada de dimensión 262.144×262.144 , denotada como un toro de Bruijn (262144,262144;6,6) 2 o simplemente B 6 . Esto podría almacenarse fácilmente en una computadora: si se imprime con píxeles de 0,1 mm de lado, dicha matriz requeriría un área de aproximadamente 26×26 metros cuadrados .
El objeto B 8 , que contiene todas las matrices binarias 8×8 y se denota (4294967296,4294967296;8,8) 2 , tiene un total de 2 64 ≈ 18,447×10 18 entradas: almacenar una matriz de este tipo requeriría 18,5 exabits, o 2,3 exabytes de almacenamiento. A la escala anterior, cubriría 429×429 kilómetros cuadrados .
La siguiente tabla ilustra el crecimiento superexponencial.
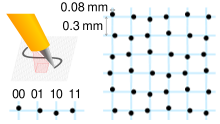
Los toros de Bruijn se utilizan en el contexto de codificación espacial, por ejemplo, para la localización de una cámara [6] , un robot [7] o un objeto tangible [8] basándose en algún patrón óptico de base.
También se utilizan como base del PuzzleBoard, [9] un objetivo de calibración de cámara óptica que agrega codificación de posición a un patrón de calibración de tablero de ajedrez. [10]
Los toros de De Bruijn se pueden utilizar para implementar papel digital , de forma similar al sistema Anoto . Sin embargo, cada celda de Anoto tiene cuatro estados posibles en lugar de dos en los toros de De Bruijn. También utiliza una secuencia repetida de De Bruijn de 6 bits con diferentes desplazamientos como columnas. [11]