Conexión Ehresmann

Construcción de geometría diferencial sobre haces de fibras

En geometría diferencial , una conexión de Ehresmann (en honor al matemático francés Charles Ehresmann , que formalizó por primera vez este concepto) es una versión de la noción de conexión , que tiene sentido en cualquier fibrado liso . En particular, no depende de la posible estructura vectorial del fibrado subyacente, pero, no obstante, las conexiones lineales pueden considerarse un caso especial. Otro caso especial importante de conexiones de Ehresmann son las conexiones principales en fibrados principales , que deben ser equivariantes en la acción principal del grupo de Lie .

Introducción

Una derivada covariante en geometría diferencial es un operador diferencial lineal que toma la derivada direccional de una sección de un fibrado vectorial de manera covariante . También permite formular una noción de una sección paralela de un fibrado en la dirección de un vector: una sección s es paralela a lo largo de un vector si . Por lo tanto, una derivada covariante proporciona al menos dos cosas: un operador diferencial y una noción de lo que significa ser paralelo en cada dirección. Una conexión de Ehresmann elimina por completo el operador diferencial y define una conexión axiomáticamente en términos de las secciones paralelas en cada dirección (Ehresmann 1950). Específicamente, una conexión de Ehresmann singulariza un subespacio vectorial de cada espacio tangente al espacio total del fibrado de fibras, llamado espacio horizontal . Una sección es entonces horizontal (es decir, paralela) en la dirección si se encuentra en un espacio horizontal. Aquí estamos considerando como una función desde la base hasta el fibrado de fibras , por lo que es entonces el empuje hacia adelante de los vectores tangentes. Los espacios horizontales juntos forman un subfibrado vectorial de . ${\displaystyle X}$ ${\displaystyle \nabla _{X}s=0}$ ${\displaystyle s}$ ${\displaystyle X}$ ${\displaystyle {\rm {d}}s(X)}$ ${\displaystyle s}$ ${\displaystyle s\colon M\to E}$ ${\displaystyle M}$ ${\displaystyle E}$ ${\displaystyle {\rm {d}}s\colon TM\to TE}$ ${\displaystyle TE}$

Esto tiene el beneficio inmediato de ser definible en una clase mucho más amplia de estructuras que los simples fibrados vectoriales. En particular, está bien definido en un fibrado general . Además, muchas de las características de la derivada covariante aún permanecen: transporte paralelo, curvatura y holonomía .

El ingrediente que falta en la conexión, además de la linealidad, es la covarianza . En las derivadas covariantes clásicas, la covarianza es una característica a posteriori de la derivada. En su construcción se especifica la ley de transformación de los símbolos de Christoffel  –que no es covariante– y, como resultado, se sigue la covarianza general de la derivada . Para una conexión de Ehresmann, es posible imponer un principio de covarianza generalizado desde el principio introduciendo un grupo de Lie que actúe sobre las fibras del haz de fibras. La condición apropiada es exigir que los espacios horizontales sean, en cierto sentido, equivariantes con respecto a la acción del grupo.

El toque final de una conexión de Ehresmann es que se puede representar como una forma diferencial , de forma muy similar al caso de una forma de conexión . Si el grupo actúa sobre las fibras y la conexión es equivariante, entonces la forma también será equivariante. Además, la forma de conexión permite una definición de curvatura también como una forma de curvatura .

Definición formal

Una conexión de Ehresmann es una elección de subespacio horizontal para cada , donde es un haz de fibras, normalmente un haz principal . ${\displaystyle H_{p}\subset T_{p}P}$ ${\displaystyle p\in P}$ ${\displaystyle P}$

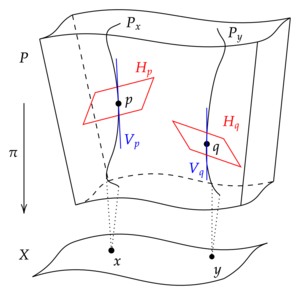
Sea un haz de fibras lisas . ^[1] Sea ${\displaystyle \pi \colon E\to M}$

${\displaystyle V=\ker(\operatorname {d} \pi \colon TE\to TM)}$

sea ​​el fibrado vertical formado por los vectores "tangentes a las fibras" de E , es decir, la fibra de V en es . Este subfibrado de está canónicamente definido incluso cuando no existe ningún subespacio canónico tangente al espacio base M . (Por supuesto, esta asimetría proviene de la propia definición de fibrado, que "solo tiene una proyección" mientras que un producto tendría dos.) ${\displaystyle e\in E}$ ${\displaystyle V_{e}=T_{e}(E_{\pi (e)})}$ ${\displaystyle TE}$ ${\displaystyle \pi \colon E\to M}$ ${\displaystyle E=M\times F}$

Definición mediante subespacios horizontales

Una conexión de Ehresmann en es un subfibrado suave de , llamado fibrado horizontal de la conexión, que es complementario a V , en el sentido de que define una descomposición de suma directa . ^[2] Con más detalle, el fibrado horizontal tiene las siguientes propiedades. ${\displaystyle E}$ ${\displaystyle H}$ ${\displaystyle TE}$ ${\displaystyle TE=H\oplus V}$

• Para cada punto , es un subespacio vectorial del espacio tangente a en , llamado subespacio horizontal de la conexión en . ${\displaystyle e\in E}$ ${\displaystyle H_{e}}$ ${\displaystyle T_{e}E}$ ${\displaystyle E}$ ${\displaystyle e}$ ${\displaystyle e}$
• ${\displaystyle H_{e}}$depende suavemente de . ${\displaystyle e}$
• Para cada , . ${\displaystyle e\in E}$ ${\displaystyle H_{e}\cap V_{e}=\{0\}}$
• Cualquier vector tangente en (para cualquier ) es la suma de un componente horizontal y vertical, de modo que . ${\displaystyle T_{e}E}$ ${\displaystyle e\in E}$ ${\displaystyle T_{e}E=H_{e}+V_{e}}$

En términos más sofisticados, tal asignación de espacios horizontales que satisfacen estas propiedades corresponde precisamente a una sección suave del haz de chorro J ¹ E → E .

Definición a través de un formulario de conexión

De manera equivalente, sea Φ la proyección sobre el fibrado vertical V a lo largo de H (de modo que H = ker Φ ). Esto se determina mediante la descomposición de suma directa anterior de TE en partes horizontales y verticales y a veces se denomina forma de conexión de la conexión de Ehresmann. Por lo tanto, Φ es un homomorfismo de fibrado vectorial de TE sobre sí mismo con las siguientes propiedades (de proyecciones en general):

• Φ2 = Φ ;^​
• Φ es la identidad en V =Im Φ .

Por el contrario, si Φ es un endomorfismo de fibrado vectorial de TE que satisface estas dos propiedades, entonces H = ker Φ es el subfibrado horizontal de una conexión de Ehresmann.

Por último, cabe señalar que Φ , al ser una aplicación lineal de cada espacio tangente en sí mismo, también puede considerarse como una forma 1 con valor TE en E . Esta será una perspectiva útil en las secciones siguientes.

Transporte paralelo mediante elevadores horizontales

Una conexión de Ehresmann también prescribe una manera de elevar curvas desde la variedad base M hasta el espacio total del haz de fibras E de modo que las tangentes a la curva sean horizontales. ^{[2] [3]} Estas elevaciones horizontales son un análogo directo del transporte paralelo para otras versiones del formalismo de conexión.

En concreto, supongamos que γ ( t ) es una curva suave en M que pasa por el punto x  =  γ (0). Sea e  ∈  E _x un punto en la fibra sobre x . Una elevación de γ a través de e es una curva en el espacio total E tal que ${\displaystyle {\tilde {\gamma }}(t)}$

${\displaystyle {\tilde {\gamma }}(0)=e}$, y ${\displaystyle \pi ({\tilde {\gamma }}(t))=\gamma (t).}$

Un ascensor es horizontal si, además, cada tangente de la curva se encuentra en el subfibrado horizontal de TE :

${\displaystyle {\tilde {\gamma }}'(t)\in H_{{\tilde {\gamma }}(t)}.}$

Se puede demostrar utilizando el teorema de rango-nulidad aplicado a π y Φ que cada vector X ∈ T _x M tiene una elevación horizontal única hacia un vector . En particular, el campo tangente a γ genera un campo vectorial horizontal en el espacio total del fibrado de pullback γ * E . Por el teorema de Picard–Lindelöf , este campo vectorial es integrable . Por lo tanto, para cualquier curva γ y punto e sobre x  =  γ (0), existe una elevación horizontal única de γ a través de e para un tiempo pequeño t . ${\displaystyle {\tilde {X}}\in T_{e}E}$

Nótese que, para conexiones generales de Ehresmann, la elevación horizontal depende de la trayectoria. Cuando dos curvas suaves en M , que coinciden en γ ₁ (0) =  γ ₂ (0) =  x ₀ y también se intersecan en otro punto x ₁  ∈  M , se elevan horizontalmente a E a través del mismo e  ∈  π ⁻¹ ( x ₀ ), generalmente pasarán por diferentes puntos de π ⁻¹ ( x ₁ ). Esto tiene consecuencias importantes para la geometría diferencial de los haces de fibras: el espacio de secciones de H no es una subálgebra de Lie del espacio de campos vectoriales en E , porque no está (en general) cerrado bajo el corchete de Lie de campos vectoriales . Esta falla de cierre bajo el corchete de Lie se mide por la curvatura .

Propiedades

Curvatura

Sea Φ una conexión de Ehresmann. Entonces la curvatura de Φ está dada por ^[2]

${\displaystyle R={\tfrac {1}{2}}[\varPhi ,\varPhi ]}$

donde [-,-] denota el corchete de Frölicher-Nijenhuis de Φ ∈ Ω ¹ ( E , TE ) consigo mismo. Por lo tanto, R ∈ Ω ² ( E , TE ) es la forma bidimensional de E con valores en TE definidos por

${\displaystyle R(X,Y)=\varPhi \left([(\mathrm {id} -\varPhi )X,(\mathrm {id} -\varPhi )Y]\right)}$,

o, en otros términos,

${\displaystyle R\left(X,Y\right)=\left[X_{H},Y_{H}\right]_{V}}$,

donde X = X _H + X _V denota la descomposición de suma directa en componentes H y V , respectivamente. A partir de esta última expresión para la curvatura, se ve que se desvanece de manera idéntica si, y solo si, el subfibrado horizontal es integrable según Frobenius . Por lo tanto, la curvatura es la condición de integrabilidad para que el subfibrado horizontal produzca secciones transversales del fibrado E → M .

La curvatura de una conexión de Ehresmann también satisface una versión de la identidad de Bianchi :

${\displaystyle \left[\varPhi ,R\right]=0}$

donde nuevamente [-,-] es el corchete de Frölicher-Nijenhuis de Φ ∈ Ω ¹ ( E , TE ) y R ∈ Ω ² ( E , TE ).

Lo completo

Una conexión Ehresmann permite que las curvas tengan elevaciones horizontales únicas a nivel local . Para una conexión Ehresmann completa , una curva puede elevarse horizontalmente en todo su dominio.

Holonomía

La planitud de la conexión corresponde localmente a la integrabilidad de Frobenius de los espacios horizontales. En el otro extremo, la curvatura no nula implica la presencia de holonomía de la conexión. ^[4]

Casos especiales

Haces principales y conexiones principales

Una forma de conexión de fibrado principal puede considerarse como un operador de proyección sobre el fibrado tangente del fibrado principal . El núcleo de la forma de conexión está dado por los subespacios horizontales para la conexión de Ehresmann asociada. ${\displaystyle \omega }$ ${\displaystyle TP}$ ${\displaystyle P}$

Supóngase que E es un fibrado principal G suave sobre M . Entonces, una conexión de Ehresmann H sobre E se dice que es una conexión principal (Ehresmann) ^[3] si es invariante con respecto a la acción de G sobre E en el sentido de que

${\displaystyle H_{eg}=\mathrm {d} (R_{g})_{e}(H_{e})}$para cualquier e ∈ E y g ∈ G ; aquí denota el diferencial de la acción correcta de g sobre E en e . ${\displaystyle \mathrm {d} (R_{g})_{e}}$

Los subgrupos de un parámetro de G actúan verticalmente sobre E . La diferencial de esta acción permite identificar el subespacio con el álgebra de Lie g del grupo G , digamos por la función . La forma de conexión Φ de la conexión de Ehresmann puede entonces verse como una 1-forma ω sobre E con valores en g definidos por ω ( X )= ι ( Φ ( X )). ${\displaystyle V_{e}}$ ${\displaystyle \iota \colon V_{e}\to {\mathfrak {g}}}$

Así reinterpretada, la forma de conexión ω satisface las dos propiedades siguientes:

• Se transforma de manera equivalente bajo la acción G : para todo h ∈ G , donde R _h ^* es el retroceso bajo la acción derecha y Ad es la representación adjunta de G en su álgebra de Lie. ${\displaystyle R_{h}^{*}\omega ={\hbox{Ad}}(h^{-1})\omega }$
• Asigna campos vectoriales verticales a sus elementos asociados del álgebra de Lie: ω ( X )= ι ( X ) para todo X ∈ V .

Por el contrario, se puede demostrar que dicha forma 1 con valor g en un fibrado principal genera una distribución horizontal que satisface las propiedades antes mencionadas.

Dada una trivialización local, se puede reducir ω a los campos vectoriales horizontales (en esta trivialización). Define una 1-forma ω' en M mediante pullback . La forma ω' determina ω completamente, pero depende de la trivialización elegida. (Esta forma también se suele llamar forma de conexión y se denota simplemente por ω .)

Fibras vectoriales y derivadas covariantes

Supóngase que E es un fibrado vectorial suave sobre M . Entonces, se dice que una conexión de Ehresmann H sobre E es una conexión lineal (de Ehresmann) si H _e depende linealmente de e ∈ E _x para cada x ∈ M . Para que esto sea preciso, sea S _λ la multiplicación escalar por λ sobre E . Entonces, H es lineal si y solo si para cualquier e ∈ E y escalar λ. ${\displaystyle H_{\lambda e}=\mathrm {d} (S_{\lambda })_{e}(H_{e})}$

Como E es un fibrado vectorial, su fibrado vertical V es isomorfo a π * E . Por lo tanto, si s es una sección de E , entonces Φ (d s ): TM → s * V = s * π * E = E . Es un morfismo de fibrado vectorial, y por lo tanto viene dado por una sección ∇ s del fibrado vectorial Hom( TM , E ). El hecho de que la conexión de Ehresmann sea lineal implica que además se verifica para cada función de la regla de Leibniz, es decir , y por lo tanto es una derivada covariante de s . ${\displaystyle f}$ ${\displaystyle M}$ ${\displaystyle \nabla (fs)=f\nabla (s)+d(f)\otimes s}$

Por el contrario, una derivada covariante ∇ en un fibrado vectorial define una conexión de Ehresmann lineal al definir H _e , para e ∈ E con x = π ( e ), como la imagen d s _x ( T _x M ) donde s es una sección de E con s ( x ) = e y ∇ _X s = 0 para todo X ∈ T _x M .

Téngase en cuenta que (por razones históricas) el término lineal , cuando se aplica a conexiones, a veces se utiliza (como la palabra afín  ; ver Conexión afín ) para referirse a conexiones definidas en el fibrado tangente o el fibrado marco .

Paquetes asociados

Una conexión de Ehresmann en un fibrado (dotado de un grupo estructural) a veces da lugar a una conexión de Ehresmann en un fibrado asociado . Por ejemplo, una conexión (lineal) en un fibrado vectorial E , pensada para dar un paralelismo de E como el anterior, induce una conexión en el fibrado asociado de tramas P E de E . A la inversa, una conexión en P E da lugar a una conexión (lineal) en E siempre que la conexión en P E sea equivariante con respecto a la acción del grupo lineal general en las tramas (y por tanto una conexión principal ). No siempre es posible que una conexión de Ehresmann induzca, de forma natural, una conexión en un fibrado asociado. Por ejemplo, una conexión de Ehresmann no equivariante en un fibrado de tramas de un fibrado vectorial puede no inducir una conexión en el fibrado vectorial.

Supóngase que E es un fibrado asociado de P , de modo que E = P × _G F . Una conexión G en E es una conexión de Ehresmann tal que el mapa de transporte paralelo τ : F _x → F _x′ está dado por una transformación G de las fibras (sobre puntos suficientemente cercanos x y x ′ en M unidos por una curva). ^[5]

Dada una conexión principal en P , se obtiene una conexión G en el haz de fibras asociado E = P × _G F mediante retroceso .

Por el contrario, dada una G -conexión en E es posible recuperar la conexión principal en el fibrado principal asociado P . Para recuperar esta conexión principal, se introduce la noción de un marco en la fibra típica F . Puesto que G es un grupo de Lie de dimensión finita ^[6] que actúa efectivamente en F , debe existir una configuración finita de puntos ( y ₁ ,..., y _m ) dentro de F tal que la G -órbita R = {( gy ₁ ,..., gy _m ) | g ∈ G } sea un espacio homogéneo principal de G . Se puede pensar en R como una generalización de la noción de un marco para la G -acción en F . Nótese que, puesto que R es un espacio homogéneo principal para G , el fibrado E ( R ) asociado a E con la fibra típica R es (equivalente a) el fibrado principal asociado a E . Pero también es un subfibrado del fibrado producto m -fold de E consigo mismo. La distribución de espacios horizontales en E induce una distribución de espacios en este fibrado producto. Dado que los mapas de transporte paralelos asociados a la conexión son mapas G , preservan el subespacio E ( R ), y por lo tanto la conexión G desciende a una conexión G principal en E ( R ).

En resumen, existe una correspondencia uno a uno (hasta la equivalencia) entre los descensos de las conexiones principales a los haces de fibras asociados y las conexiones G en los haces de fibras asociados. Por esta razón, en la categoría de haces de fibras con un grupo de estructura G , la conexión principal contiene toda la información relevante para las conexiones G en los haces asociados. Por lo tanto, a menos que haya una razón imperiosa para considerar las conexiones en los haces asociados (como la hay, por ejemplo, en el caso de las conexiones de Cartan ), generalmente se trabaja directamente con la conexión principal.

Notas

1. Estas consideraciones se aplican igualmente bien a la situación más general en la que es una inmersión sobreyectiva : es decir, E es un fibrado sobre M . En una generalización alternativa, debido a Lang (1999) y Eliason (1967), se permite que E y M sean variedades de Banach , con E un fibrado sobre M como el anterior. ${\displaystyle \pi \colon E\to M}$
2. Kolář, Michor y Slovák (1993), pág.  ^{[ página necesaria ]} .
3. Kobayashi & Nomizu (1996a), p.  ^{[ página necesaria ]} , Vol. 1.
4. La holonomía para las conexiones de Ehresmann en los haces de fibras a veces se denomina holonomía de Ehresmann-Reeb u holonomía de la hoja en referencia al primer estudio detallado que utilizó conexiones de Ehresmann para estudiar las foliaciones en (Reeb 1952)
5. Véase también Lumiste (2001b), "Conexiones en una variedad".
6. Para mayor comodidad, suponemos que G es de dimensión finita, aunque esta suposición puede descartarse con seguridad con modificaciones menores.

Referencias

• Ehresmann, Charles (1950), Les connexions infinitésimales dans un espace fibré différentiable (PDF) , Colloque de Topologie, Bruselas, Georges Thone, Lieja; Masson & cie, París, págs. 29-55
• Ehresmann, Charles (1952), Les connexions infinitésimales dans un espace fibré différentiable (PDF) , Séminaire N. Bourbaki, vol. 24, págs. 153-168
• Eliason, H (1967), "Geometría de variedades de mapas", Journal of Differential Geometry , 1 : 169–194
• Kobayashi, Shoshichi (1957), "Teoría de las conexiones", Ann. Mat. Pura Appl. , 43 : 119–194, doi : 10.1007/BF02411907 , MR  0096276, S2CID  120972987
• Kobayashi, Shoshichi ; Nomizu, Katsumi (1996a), Fundamentos de geometría diferencial , vol. 1 (Nueva ed.), Wiley-Interscience, ISBN 0-471-15733-3
• Kobayashi, Shoshichi ; Nomizu, Katsumi (1996b), Fundamentos de la geometría diferencial , vol. 2 (Nueva ed.), Wiley-Interscience, ISBN 978-0-471-15732-8
• Kolář, Ivan; Michor, Peter; Slovák, Jan (1993), Operadores naturales en geometría diferencial (PDF) , Springer-Verlag, archivado desde el original (PDF) el 2017-03-30 , consultado el 2007-04-25
• Lang, Serge (1999), Fundamentos de geometría diferencial , Springer-Verlag, ISBN 0-387-98593-X
• Lumiste, Ülo (2001a) [1994], "Conexión en un haz de fibras", Enciclopedia de Matemáticas , EMS Press
• Lumiste, Ülo (2001b) [1994], "Conexiones en una variedad", Enciclopedia de Matemáticas , EMS Press
• Reeb, Georges (1952), Sur surees propriétés topologiques des variétés feuilletées , París: Herman

Lectura adicional

• Raoul Bott (1970) "Obstrucción topológica a la integrabilidad", Proc. Symp. Pure Math. , 16 Amer. Math. Soc., Providence, RI.
• Kubarski, Jan; Pradines, Jean; Rybicki, Tomasz; Wolak, Robert, eds. (2007). Geometría y topología de variedades: el legado matemático de Charles Ehresmann con motivo del centenario de su cumpleaños. Publicaciones del Centro Banach. Vol. 76. Varsovia: Academia Polaca de Ciencias . MR  2284825.