Una superficie sólida ideal es plana, rígida, perfectamente lisa y químicamente homogénea, y tiene una histéresis de ángulo de contacto cero. La histéresis cero implica que los ángulos de contacto de avance y retroceso son iguales.
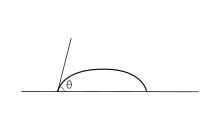
En otras palabras, solo existe un ángulo de contacto termodinámicamente estable . Cuando se coloca una gota de líquido sobre una superficie de este tipo, se forma el ángulo de contacto característico que se muestra en la figura 1. Además, en una superficie ideal, la gota volverá a su forma original si se la altera. [1] Las siguientes derivaciones se aplican solo a superficies sólidas ideales; solo son válidas para el estado en el que las interfaces no se mueven y la línea límite de fase existe en equilibrio.

La figura 3 muestra la línea de contacto donde se encuentran las tres fases. En equilibrio , la fuerza neta por unidad de longitud que actúa a lo largo de la línea límite entre las tres fases debe ser cero. Los componentes de la fuerza neta en la dirección a lo largo de cada una de las interfaces se dan por:
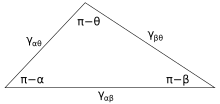
donde α, β y θ son los ángulos mostrados y γ ij es la energía superficial entre las dos fases indicadas. Estas relaciones también se pueden expresar mediante un análogo a un triángulo conocido como triángulo de Neumann, que se muestra en la Figura 4. El triángulo de Neumann es consistente con la restricción geométrica de que , y al aplicarle la ley de senos y la ley de cosenos se producen relaciones que describen cómo los ángulos interfaciales dependen de las relaciones de las energías superficiales. [2]
Como estas tres energías superficiales forman los lados de un triángulo , están limitadas por las desigualdades del triángulo, γ ij < γ jk + γ ik, lo que significa que ninguna de las tensiones superficiales puede superar la suma de las otras dos. Si se ponen en contacto tres fluidos con energías superficiales que no siguen estas desigualdades, no existirá ninguna configuración de equilibrio coherente con la Figura 3.
Si la fase β se reemplaza por una superficie rígida plana, como se muestra en la Figura 5, entonces β = π, y la segunda ecuación de fuerza neta se simplifica a la ecuación de Young, [3]

que relaciona las tensiones superficiales entre las tres fases: sólido , líquido y gaseoso . Posteriormente, esto predice el ángulo de contacto de una gota de líquido sobre una superficie sólida a partir del conocimiento de las tres energías superficiales involucradas. Esta ecuación también se aplica si la fase "gas" es otro líquido, inmiscible con la gota de la primera fase "líquida".
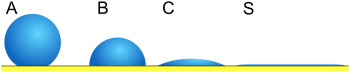
La ecuación de Young supone una superficie perfectamente plana y rígida. En muchos casos, las superficies están lejos de esta situación ideal, y aquí se consideran dos: el caso de superficies rugosas y el caso de superficies lisas que aún son reales (finitamente rígidas). Incluso en una superficie perfectamente lisa, una gota asumirá un amplio espectro de ángulos de contacto que van desde el llamado ángulo de contacto de avance, , hasta el llamado ángulo de contacto de retroceso, . El ángulo de contacto de equilibrio ( ) se puede calcular a partir de y como lo demostró Tadmor [5] como,
dónde
La ecuación de Young-Dupré (Thomas Young 1805, Lewis Dupré 1855) dicta que ni γ SG ni γ SL pueden ser mayores que la suma de las otras dos energías superficiales. La consecuencia de esta restricción es la predicción de humectación completa cuando γ SG > γ SL + γ LG y humectación cero cuando γ SL > γ SG + γ LG . La falta de una solución para la ecuación de Young-Dupré es un indicador de que no existe una configuración de equilibrio con un ángulo de contacto entre 0 y 180° para esas situaciones.
Un parámetro útil para medir la humectación es el parámetro de propagación S ,
Cuando S > 0, el líquido humedece completamente la superficie (humectación completa). Cuando S < 0, se produce una humectación parcial.
Combinando la definición del parámetro de propagación con la relación de Young se obtiene la ecuación de Young-Dupré:
que sólo tiene soluciones físicas para θ cuando S < 0.