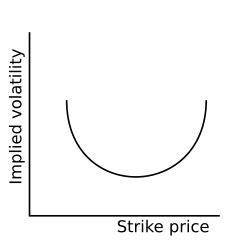
Las sonrisas de volatilidad son patrones de volatilidad implícita que surgen al fijar el precio de las opciones financieras . Es un parámetro (volatilidad implícita) que se debe modificar para que la fórmula de Black-Scholes se ajuste a los precios del mercado. En particular, para un vencimiento determinado, las opciones cuyo precio de ejercicio difiere sustancialmente del precio del activo subyacente exigen precios más altos (y, por lo tanto, volatilidades implícitas) que lo que sugieren los modelos de fijación de precios de opciones estándar. Se dice que estas opciones están en un nivel de dinero muy alto o fuera del dinero .
La representación gráfica de las volatilidades implícitas frente a los precios de ejercicio para un vencimiento determinado produce una "sonrisa" sesgada en lugar de la superficie plana esperada. El patrón difiere en los distintos mercados. Las opciones sobre acciones negociadas en los mercados estadounidenses no mostraban una sonrisa de volatilidad antes del colapso de 1987, pero comenzaron a mostrarla después. [1] Se cree que las reevaluaciones de los inversores de las probabilidades de cola gruesa han llevado a precios más altos para las opciones fuera del dinero. Esta anomalía implica deficiencias en el modelo estándar de fijación de precios de opciones de Black-Scholes que supone una volatilidad constante y distribuciones log-normales de los rendimientos de los activos subyacentes. Sin embargo, las distribuciones empíricas de los rendimientos de los activos tienden a exhibir colas gruesas ( curtosis ) y sesgo. La modelización de la sonrisa de la volatilidad es un área activa de investigación en finanzas cuantitativas , y mejores modelos de fijación de precios, como el modelo de volatilidad estocástica, abordan parcialmente esta cuestión.
Un concepto relacionado es el de la estructura temporal de la volatilidad , que describe cómo difiere la volatilidad (implícita) para opciones relacionadas con diferentes vencimientos. Una superficie de volatilidad implícita es un gráfico tridimensional que representa la sonrisa de volatilidad y la estructura temporal de la volatilidad en una superficie tridimensional consolidada para todas las opciones sobre un activo subyacente determinado.
En el modelo Black-Scholes , el valor teórico de una opción convencional es una función creciente monótona de la volatilidad del activo subyacente. Esto significa que, por lo general, es posible calcular una volatilidad implícita única a partir de un precio de mercado determinado para una opción. Esta volatilidad implícita se considera mejor como un reajuste de los precios de las opciones que hace que las comparaciones entre diferentes precios de ejercicio, vencimientos y activos subyacentes sean más fáciles e intuitivas.
Cuando se representa gráficamente la volatilidad implícita frente al precio de ejercicio , el gráfico resultante suele tener una pendiente descendente en el caso de los mercados de acciones, o una forma de valle en el caso de los mercados de divisas. En el caso de los mercados en los que el gráfico tiene una pendiente descendente, como en el caso de las opciones sobre acciones, se suele utilizar el término " desviación de la volatilidad ". En el caso de otros mercados, como las opciones sobre divisas o las opciones sobre índices bursátiles, en los que el gráfico típico se inclina hacia arriba en cualquiera de los extremos, se utiliza el término más conocido " sonrisa de volatilidad ". Por ejemplo, la volatilidad implícita de las opciones sobre acciones al alza (es decir, con un precio de ejercicio alto) suele ser inferior a la de las opciones sobre acciones al dinero. Sin embargo, las volatilidades implícitas de las opciones sobre contratos de divisas tienden a aumentar tanto en dirección descendente como ascendente. En los mercados de acciones, a menudo se observa una pequeña sonrisa inclinada cerca del dinero como una torcedura en el gráfico general de volatilidad implícita con pendiente descendente. A veces se utiliza el término "sonrisa burlona" para describir una sonrisa sesgada.
Los profesionales del mercado utilizan el término volatilidad implícita para indicar el parámetro de volatilidad de las opciones ATM (at the money). Los ajustes a este valor se realizan incorporando los valores de reversión de riesgo y sesgos para determinar la medida de volatilidad real que se puede utilizar para las opciones con un delta que no sea 50.
dónde:
Las reversiones de riesgo generalmente se cotizan como una reversión de riesgo delta x % y esencialmente son una opción de compra larga con delta x % y una opción de venta corta con delta x %.
Butterfly , por otro lado, es una estrategia que consiste en: − y % delta fly, que significa compra larga de y % delta, venta larga de y % delta, compra corta de una opción ATM y venta corta de una opción ATM (forma de sombrero pequeño).
Es útil notar que la volatilidad implícita está relacionada con la volatilidad histórica , pero las dos son distintas. La volatilidad histórica es una medida directa del movimiento del precio del subyacente (volatilidad realizada) a lo largo de la historia reciente (por ejemplo, un período de 21 días anterior). La volatilidad implícita, por el contrario, está determinada por el precio de mercado del contrato derivado en sí, y no del subyacente. Por lo tanto, diferentes contratos derivados sobre el mismo subyacente tienen diferentes volatilidades implícitas en función de su propia dinámica de oferta y demanda . Por ejemplo, la opción de compra de IBM , con un precio de ejercicio de $100 y que vence en 6 meses, puede tener una volatilidad implícita del 18%, mientras que la opción de venta con un precio de ejercicio de $105 y que vence en 1 mes puede tener una volatilidad implícita del 21%. Al mismo tiempo, la volatilidad histórica de IBM para el período de 21 días anterior podría ser del 17% (todas las volatilidades se expresan en movimientos porcentuales anualizados).
En el caso de las opciones con distintos vencimientos, también observamos diferencias características en la volatilidad implícita. Sin embargo, en este caso, el efecto dominante está relacionado con el impacto implícito en el mercado de los próximos acontecimientos. Por ejemplo, se ha observado que la volatilidad realizada de los precios de las acciones aumenta significativamente el día en que una empresa informa sus resultados. En consecuencia, observamos que la volatilidad implícita de las opciones aumentará durante el período anterior al anuncio de los resultados y luego volverá a caer tan pronto como el precio de las acciones absorba la nueva información. Las opciones que vencen antes muestran una mayor oscilación en la volatilidad implícita (a veces denominada "volumen de volatilidad") que las opciones con vencimientos más largos.
Otros mercados de opciones muestran un comportamiento diferente. Por ejemplo, las opciones sobre futuros de materias primas suelen mostrar una mayor volatilidad implícita justo antes del anuncio de las previsiones de cosechas. Las opciones sobre futuros de letras del Tesoro de Estados Unidos muestran una mayor volatilidad implícita justo antes de las reuniones de la Junta de la Reserva Federal (cuando se anuncian los cambios en las tasas de interés a corto plazo).
El mercado incorpora muchos otros tipos de eventos en la estructura temporal de la volatilidad. Por ejemplo, el impacto de los próximos resultados de un ensayo de un medicamento puede provocar oscilaciones implícitas de la volatilidad en las acciones farmacéuticas. La fecha prevista de resolución de un litigio de patentes puede afectar a las acciones tecnológicas, etc.
Las estructuras de términos de volatilidad enumeran la relación entre las volatilidades implícitas y el tiempo hasta el vencimiento. Las estructuras de términos brindan otro método para que los operadores evalúen las opciones baratas o caras.
A menudo resulta útil representar gráficamente la volatilidad implícita en función del precio de ejercicio y del tiempo hasta el vencimiento. [2] El resultado es una superficie curva bidimensional representada en tres dimensiones, en la que la volatilidad implícita actual del mercado ( eje z ) para todas las opciones sobre el activo subyacente se representa gráficamente frente al precio ( eje y ) y el tiempo hasta el vencimiento ( eje x "DTM"). Esto define la superficie de volatilidad implícita absoluta ; al cambiar las coordenadas de modo que el precio se reemplace por delta se obtiene la superficie de volatilidad implícita relativa .
La superficie de volatilidad implícita muestra simultáneamente tanto la sonrisa de volatilidad como la estructura temporal de la volatilidad. Los operadores de opciones utilizan un gráfico de volatilidad implícita para determinar rápidamente la forma de la superficie de volatilidad implícita y para identificar las áreas en las que la pendiente del gráfico (y, por lo tanto, las volatilidades implícitas relativas) parecen estar desalineadas.
El gráfico muestra una superficie de volatilidad implícita para todas las opciones de venta sobre un precio de acción subyacente en particular. El eje z representa la volatilidad implícita en porcentaje, y los ejes x e y representan el delta de la opción y los días hasta el vencimiento. Tenga en cuenta que para mantener la paridad entre opciones de venta y compra , una opción de venta con delta 20 debe tener la misma volatilidad implícita que una opción de compra con delta 80. Para esta superficie, podemos ver que el símbolo subyacente tiene tanto una inclinación de volatilidad (una inclinación a lo largo del eje delta), como una estructura de plazo de volatilidad que indica un evento anticipado en el futuro cercano.
Una superficie de volatilidad implícita es estática : describe las volatilidades implícitas en un momento dado. La forma en que la superficie cambia a medida que cambia el spot se denomina evolución de la superficie de volatilidad implícita .
Las heurísticas comunes incluyen:
Entonces, si el precio al contado se mueve de $100 a $120, el strike fijo predeciría que la volatilidad implícita de una opción con strike de $120 sería la misma que antes del movimiento (aunque haya pasado de ser OTM a ATM), mientras que el delta fijo predeciría que la volatilidad implícita de la opción con strike de $120 sería la misma que la volatilidad implícita de la opción con strike de $100 antes del movimiento (ya que ambas son ATM en ese momento).
Los métodos para modelar la sonrisa de la volatilidad incluyen modelos de volatilidad estocástica y modelos de volatilidad local . Para un análisis de los diversos enfoques alternativos desarrollados aquí, véase Economía financiera § Desafíos y críticas y Modelo de Black-Scholes § La sonrisa de la volatilidad .