En teoría de computabilidad , una secuencia de Specker es una secuencia computable , monótonamente creciente y acotada de números racionales cuyo supremo no es un número real computable . El primer ejemplo de una secuencia de este tipo fue construido por Ernst Specker (1949).
La existencia de secuencias de Specker tiene consecuencias para el análisis computable . El hecho de que tales secuencias existan significa que la colección de todos los números reales computables no satisface el principio de límite superior mínimo del análisis real, incluso cuando se consideran solo secuencias computables. Una forma común de resolver esta dificultad es considerar solo secuencias que estén acompañadas por un módulo de convergencia ; ninguna secuencia de Specker tiene un módulo de convergencia computable. De manera más general, una secuencia de Specker se denomina contraejemplo recursivo del principio de límite superior mínimo, es decir, una construcción que muestra que este teorema es falso cuando se restringe a los reales computables.
El principio de límite superior mínimo también ha sido analizado en el programa de matemáticas inversas , donde se ha determinado la fuerza exacta de este principio. En la terminología de ese programa, el principio de límite superior mínimo es equivalente a ACA 0 sobre RCA 0. De hecho, la prueba de la implicación hacia delante, es decir, que el principio de límite superior mínimo implica ACA 0 , se obtiene fácilmente a partir de la prueba del libro de texto (véase Simpson, 1999) de la no computabilidad del supremo en el principio de límite superior mínimo.
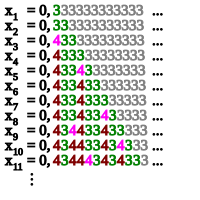
La siguiente construcción está descrita por Kushner (1984). Sea A cualquier conjunto recursivamente enumerable de números naturales que no sea decidible , y sea ( a i ) una enumeración computable de A sin repetición. Defina una secuencia ( q n ) de números racionales con la regla
Está claro que cada q n es no negativo y racional, y que la secuencia q n es estrictamente creciente. Además, como a i no tiene repetición, es posible estimar cada q n respecto de la serie
Por lo tanto, la secuencia ( q n ) está acotada superiormente por 1. Clásicamente, esto significa que q n tiene un supremo x .
Se muestra que x no es un número real computable. La prueba utiliza un hecho particular sobre los números reales computables. Si x fuera computable, entonces habría una función computable r ( n ) tal que | q j - q i | < 1/ n para todo i , j > r ( n ). Para calcular r , compare la expansión binaria de x con la expansión binaria de q i para valores cada vez mayores de i . La definición de q i hace que un solo dígito binario vaya de 0 a 1 cada vez que i aumenta en 1. Por lo tanto, habrá algún n donde un segmento inicial lo suficientemente grande de x ya ha sido determinado por q n como para que nunca se puedan activar dígitos binarios adicionales en ese segmento, lo que conduce a una estimación de la distancia entre q i y q j para i , j > n .
Si se pudiera calcular una función r , se llegaría a un procedimiento de decisión para A , como el siguiente: dada una entrada k , se calcula r (2 k +1 ). Si k apareciera en la secuencia ( a i ), esto haría que la secuencia ( q i ) aumentara en 2 − k -1 , pero esto no puede suceder una vez que todos los elementos de ( q i ) están a una distancia de 2 − k -1 entre sí. Por lo tanto, si se va a enumerar k en a i , se debe enumerar para un valor de i menor que r (2 k +1 ). Esto deja un número finito de lugares posibles donde se podría enumerar k . Para completar el procedimiento de decisión, se deben verificar estos de manera efectiva y luego se devuelve 0 o 1 dependiendo de si se encuentra k .